I. THEORY EVALUATION
In the 60-80-ies of the XX century polynomial splines the whole degree m [1,9] are wide spread to solve problems of approximation of continuous functions. Denote a spline function of one variable x as Sm(x) (one-S-spline). Such a spline is based on the grid nodes xi located at the axis of abscissa (i=0,1, …, n):
and has the following properties[1]:
-
Continuity on any closed interval [a,b] together with their derivatives up to some order p.
-
The matching polynomial of the same degree m on each interior interval [xi,xi+1] the interval [a,b]:
The difference d=m−p is called the defect of the spline. One should distinguish between interpolation and smoothing splines. Construction of the interpolation splines of degree m ≥ 2 is connected with the need of solving SLAE, in which connection the edge (boundary) conditions have an important role in algorithms for computing the coefficients.
In tasks of reproduction of experimental data dependences of the measurement results are known only approximately. With a large amount of data usually require complex recovery algorithms and valuable time resources. To rich our destination smoothing splines are having important role. They can be built in accordance with different criteria of approximation, e.g. by minimizing function of the form[2,5,7]:
And
where αi, α are positive numbers. In these formulas, the sum of squared deviations of the spline from the function values at the nodes is combined with the degree of smoothness [1,8,9].
In the theory of approximation by splines the fundamental importance is the concept of the basis as system of base functions. If the grid of nodes is set (1), then on an interval [a,b] any S-spline of degree m of the defect d=1 can be represented as a sum of basis splines (B-splines) with weight factors coefficients bi:
where splines Bm,i represent a finite, piecewise polynomial functions, moreover, are defined on compact media. They must satisfy the following conditions:
B-splines are different from zero on the intervals of length (m+1) h and are linearly independent on [a,b]. To approximate the function off(x)by a sequence of B-splines, it requires to insert additional nodes in the amount of 2m (m nodes on the left and the same number of nodes on the right) outside the interval [a, b].
B-spline of any degree m ≥ 1 is constructed according to a recursive convolution formula [1]:
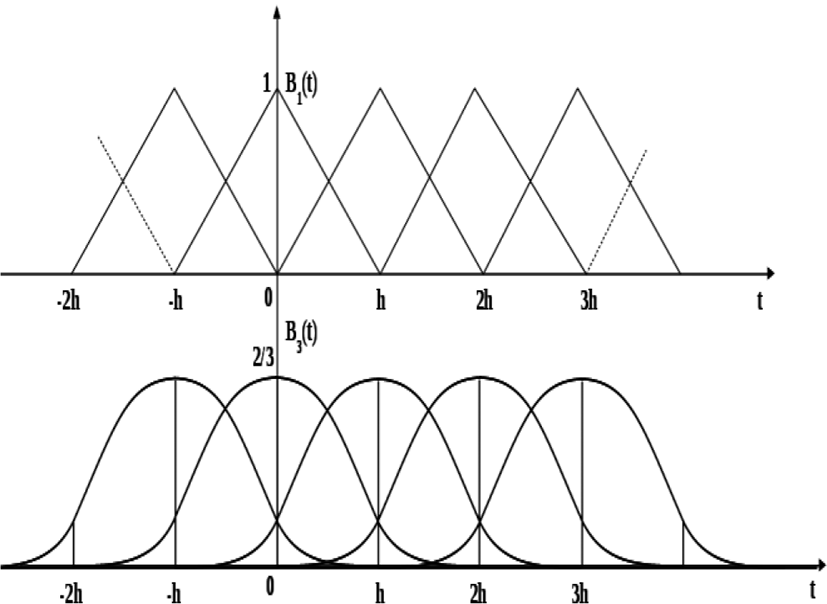
If the distances between adjacent nodes of the spline are the same, i.e.xi+1−xi=h = const. Here, h value is the step of approximation (interpolation) for an equal mesh. We give analytical expressions for b-splines of small degrees of odd (1st and 3rd) in the vicinity of the origin x=0 at equally spaced nodes with the step h=1:
For b-spline of the 1st degree (medium - cut [−1,1]):
For b-spline of the 3rd degree (media - cut [−2,2]):
Graphics of sequences of B-splines of these two degrees are shown in Figure 1.
Matrix systems of linear algebraic equations (SLAE) needed to calculate the b-coefficients of the interpolation cubic spline is obtained tridiagonal with dominant main diagonal. It is nonspecial and the computational process of obtaining coefficients is stable. The system of equations also can be solved by using Thomas method [9]. The corresponding matrix to obtain the coefficients of the smoothing spline contains of five diagonals. The systems of equations with such matrices are also easily solved by Thomas method. Along with such options in the theory of splines, so-called “local” smoothing (averaging) algorithms are worked out, that do not require the solution of SLAE of high orders, which leads to a reduction of processing time of the original data sets [8,9]. The required amount of computation is only slightly dependent on the number of mesh nodes and determined almost only by the degree of the spline. It turns out much smaller than in the interpolation, and the results are characterized by only a marginal loss in accuracy. For cubic splines the convergence of the process of approximation to an accurate result for each step is estimated as O(h4).
Examples of local smoothing formulas for calculating the b-coefficients for interior points of the interval (a,b) are [1,4,6,7]:
For splines of the 3rd degree:
- averaging three values of the function f(x):
- averaged over five values:
For splines of the 5th degree:
- averaged over five values:
Such formulas retain the properties of smoothness of the approximating spline and the same order of convergence, interpolation and approximation. The coefficients do not depend on values of functions, quite remote from the current node number. They have a symmetrical appearance, but it is valid only for interior points of the interval. The coefficients for the boundary and neighboring samples are determined by separate interpolation formulas. You may also need extra nodes outside the segment. For example, the formula of three values (9) for the coefficients of cubic B-splines can be complemented with expressions for the boundary points [6]:
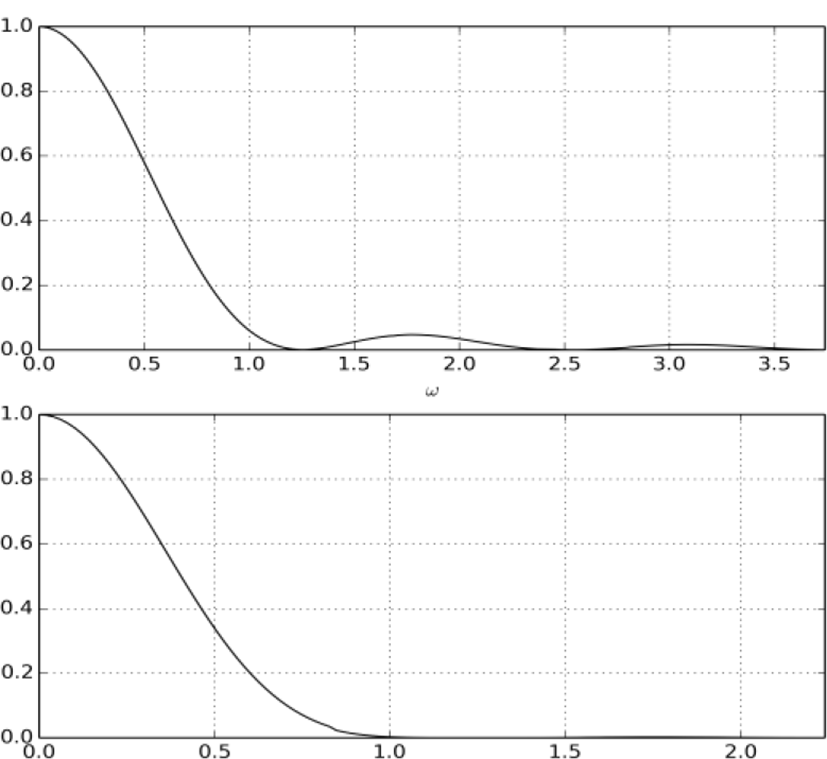
Transform of FurieB-splines of any degree m result of the formula in the following form [5]:
where A – amplitude b-spline.
Graphics of modules of spectral density of B-splines of the first and third degrees are shown in Figure 2.
B-splines represent a natural system of basic functions, with which can be created the entire reasonableness, the necessary length of discrete samples of continuous signals. First, they have their own internal grid nodes. Secondly, analytical expressions for their spectral characteristics, represented by the formula (13), have many similarities with the expression for a General member sinc(x) of the cardinal number (1.1) which was used in the theory of communication by V. A. Kotelnikov and Claude Shennon in obtaining the main theorem of samples. The difference lies in that for fixing the sample zeroes are allocated ωc=π/h frequency response functions Fm(ω), but not zero of cardinal number, and that the degree m of the transcendental function can be greater than unity. Theoretically, the functions of the frequency argument in the formula (13) are defined and not equal to zero in the entire x-axis except for a countable set of points.
The main difference, not counting the exponent m ≥ 1, is that a continuous variable can be the frequency ω and the discrete values of h steps are\ automatically recorded, as an essential principle of the theory of splines as finite basis elements, i.e. the arrangement of their nodes. And exactly the same as f(x,ω)=sinc(x,ω), the functions Fm(ω) theoretically have an infinite number of zeros.
Let’s use the above formula (5) for the spectral energy:
and apply the equality of Parseval for continuous signals [9]:
We also use the term “energy Eεon the level ε”. It means the value of the energy integral for functions integral with square, characterized by the value ε of the total energy of the signal.
Between different types of spectral energy in the frequency domain there is a close correlation:
The spectra F(ω) and Fas(ω) due to the finiteness of both signals and elements of the basis are infinite. Energy of a finite sequence of B-splines defined on a compact media is terminal. This energy as a function of frequency, can be divided into two parts – low frequency ELf(ω)and high frequency Ehf(ω), which consists of two components:
The boundary frequency between the low and high frequency part of the energy spectrum, as in the previous chapter, you can designate itωc. Then we can use a theorem of mathematical analysis, which is known as the theorem on integral inequalities [3]:
Apply it to assess the share of the high energy part of the spectrum Ehf(ω) compared with the total energy of the signal. You will get a sequence of transformations [4,6,8]:
where K1 – coefficient depending on the number of knots of the spline, i.e. the length of the discrete samples of the signal f(x).
The integral on the right side (20), refers to the number of table integrals and is easily calculated in quadrature. In the result we get estimation for high-frequency energy:
From this expression, it can be concluded that the energy of high frequency part of the spectrum of a sequence of B-splines approximating signal is proportional to the step size of the sampling multiplier, dependent on the degree of the spline.
V. CONCLUSION
The material presented shows that when solving problems in the theory of signal counts, methods of spline-functions with compact support can give definite advantages over a theory using the principle of finite spectrum. The principle of the finiteness of signal carriers is at the forefront, which leads to the infiniteness of the spectra and requires detailed estimates of the accuracy of calculations of the energy characteristics.
The advantage of the method of finite basis functions, in contrast to the practice of interpolation approximations considered in applications of the theory of functions with finite spectrum, is the ability to restore signals according to various criteria - like interpolation and quadratic functional minimization criteria and others