Ellipsoid Modeling Method for Coding of Face Depth Picture

I. INTRODUCTION

Recently the face recognition technology for identity recognition is increasing. In particular, the face recognition methods based on the color image [1-5] have been researched. However, the face recognition method based on color image is vulnerable to false authentication attempts using photographs. To solve this problem, the face recognition methods based on the depth image whose pixels have distances from the camera has been proposed [6-7]. This method recognizes the face by using LBP (Local Binary Patterns) of a depth picture with a face. This method improved a face recognition accuracy in dark environment compared to methods based on color image, and false authentication attempt can be prevented.

The processes of identity recognition system have a face capturing step, a face detection step, and a face recognition step. In the face detection step, the existence of a face in the image is determined and an area of a face is detected. In the face recognition step, features of the face are extracted and compared to stored face features. When a face picture is captured by an embedded device, it is inefficient to perform the face recognition step on the same device because its processor does not perform well. Therefore, the step of face recognition that are extracting and comparing face features is efficient to be processed separately in a high performance device. In order to implement the real time system for the face recognition, it is important to improve the speed of face picture transmission between an embedded device for capturing depth pictures and a device for extracting facial features. The improvement of the transmission speed can be achieved by efficiently compressing the depth pictures including the face.

Several methods for compressing depth video through conventional video coding standards for color video have been studied [8-13]. However, the coding schemes designed for color video are not directly applicable to the depth video since the number of bits for a depth pixel is higher than 8 bits of a color pixel.

The depth picture can be regarded as representation of surfaces. Therefore, the depth picture can be predicted by plane modeling [14] or spherical surface [15]. In order to predict a face depth picture, the ellipsoid modeling is proposed because the shape of the face is close to an ellipsoid.

The human face is similar to an ellipsoid. Therefore, the depth picture that is captured the face is also similar to the ellipsoid surface. An amount of transmission information of the face depth picture can be reduced by predicting the picture through modeled the ellipsoid. In this paper, we propose a method of ellipsoid modeling for the face depth picture. The nearest ellipsoid is modeled using depth pixels in the face picture. Depth pixel values are predicted through the modeled ellipsoid.

II. ELLIPSOID MODELING FOR FACE DEPTH PICTURE

2.1 Transformation of image coordinates to 3D coordinates through depth value

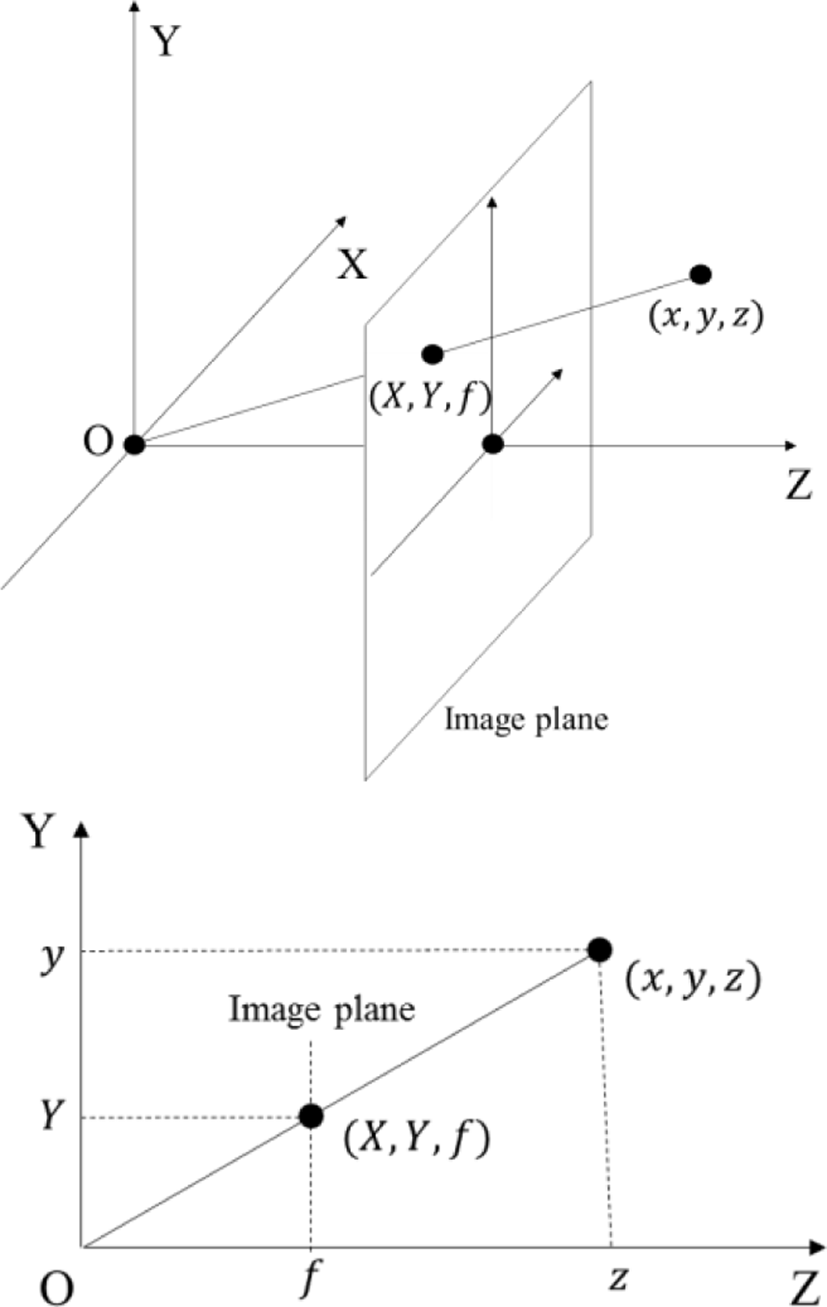
A camera is a kind of device used to translate coordinates. A point in the real world is projected into a pixel on a plane, which is an image captured by the camera. The pinhole camera model assumes that a point in real world passes through the pinhole and is projected into a temporary image plane. In the actual pinhole camera, the projected image plane is located behind the pinhole plane back so the image is overturned. However, the pinhole camera model assumes that the image plane is placed in the front of the pinhole. A point in 3D camera coordinate system, whose origin is set to the camera and direction of z-axis is set to the optical axis of the camera, projected onto a point in the image plane as shown in Fig. 1. In this case, x- and y-coordinates of the projected point are defined as the coordinates of its pixel. The relationship between the 3D camera coordinates and the image coordinates as follows:

$$\begin{array}{l}z:f=x:X\to x=\frac{Xz}{f}\hfill \\ z:f=y:Y\to y=\frac{Yz}{f},\hfill \end{array}$$

(1)

where f means a focal length, which is a distance between the image plane and the camera. Therefore, the image coordinates (X, Y) of a pixel with a depth value d(X, Y) are transformed into 3D camera coordinates (x, y, z) as follows:

$$x=\frac{X}{f}d\left(X,Y\right),y=\frac{Y}{f}d\left(X,Y\right),z=d\left(X,Y\right).$$

(2)

Fig. 1. Relationship between camera and image coordinates in pinhole camera model.

Download Original Figure

2.2 Detection of nose tip from face depth picture

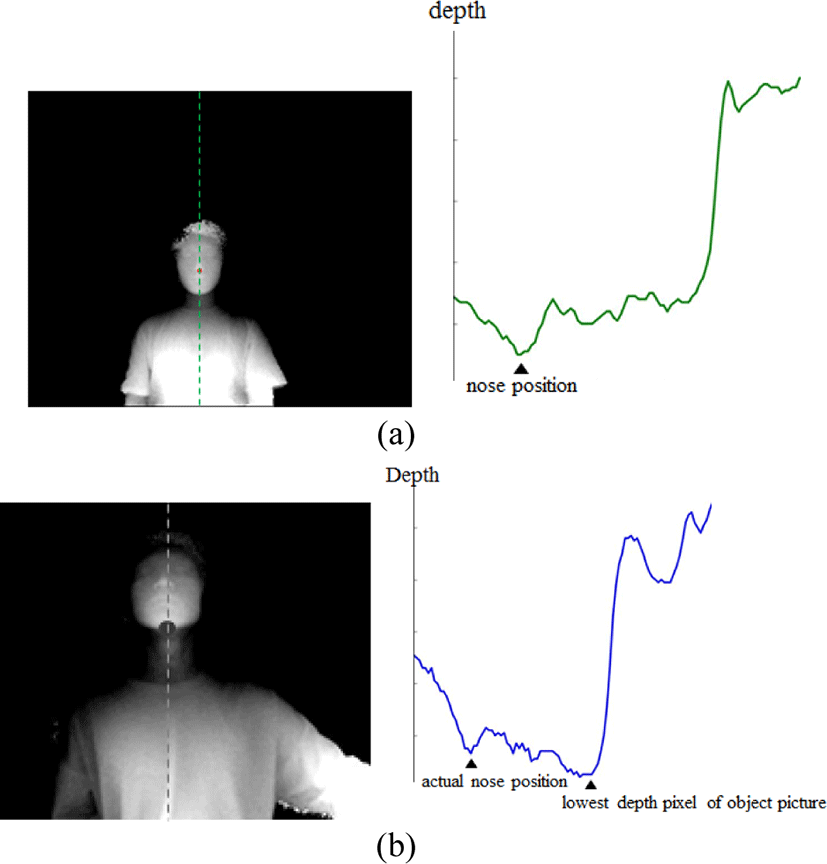
A human face is similar to an ellipsoid. A nose is close to the center of the face. Therefore, it is important to detect the nose in a face depth picture for the ellipsoid modeling.

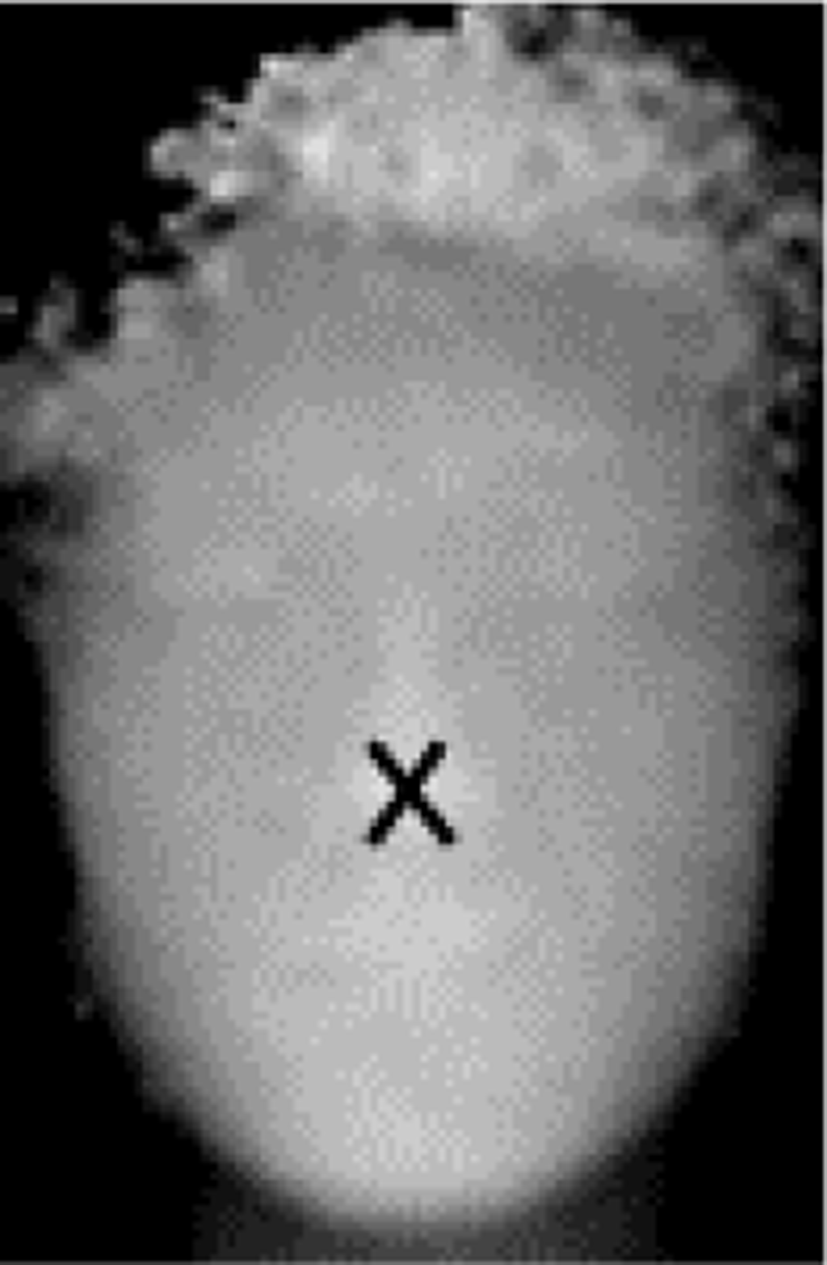
In the face depth picture, a nose tip is usually the closest distance from the camera so the depth of the nose tip has a minimum value when the face is aligned with the direction of the camera capturing as shown in Fig. 2 (a). However, the other point such as jaw can have a minimum value in the depth picture as shown in Fig. 2 (b). In order to solve this problem, points having a minimum depth value in local area instead of whole picture area are found as candidates of the nose tip.

Fig. 2. Depth value of nose tip according to face poses. (a) in case of frontal capturing, and (b) in case of capturing from below.

Download Original Figure

The depth values decrease continuously as it gets closer to the nose tip. Therefore, candidates of nose tip can be found by searching pixels each which has the smallest depth value in a local area. Each pixel is searched vertically and horizontally to the region performed in order to find a pixel whose N consecutive pixels in the left and right directions become larger depth value than the preceding pixel through following equation:

(3)

where p_i means a searched pixel and p_i±k means a kth pixel from p_i in the vertical or the horizontal directions.

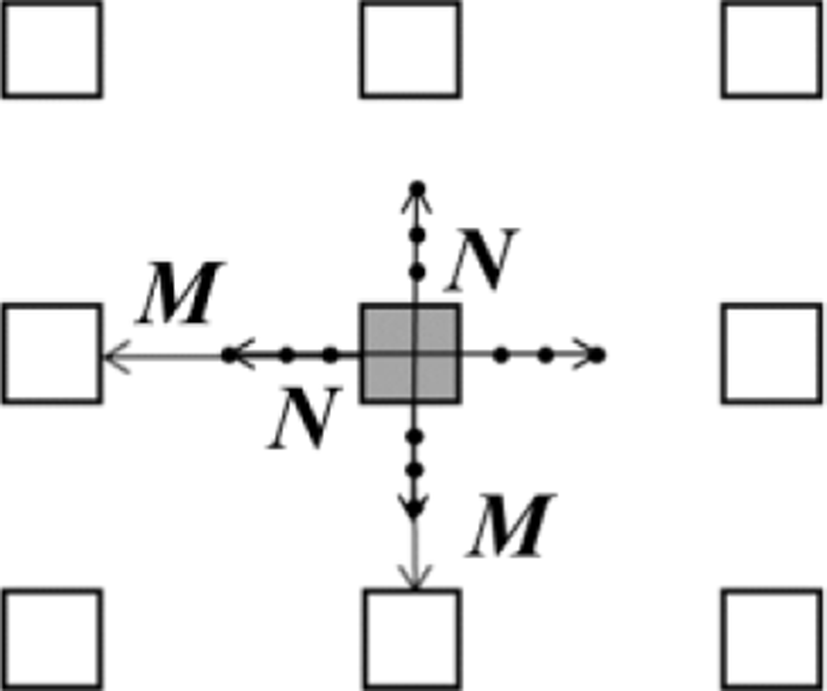
In order to detect actual nose tip, it is necessary to compare the neighboring pixels of the candidates. Each candidate is compared with depth values of surrounding pixels. Each surrounding pixel whose distance is M (M > N) pixels are compared with the candidate point as shown in Fig. 3. If a depth of a candidate point is less than every surrounding pixel, the candidate point is determined as the actual nose tip as shown in Fig. 4.

Fig. 3. Comparison of depth value with surrounding pixels.

Download Original Figure

Fig. 4. Found nose point from face depth picture.

Download Original Figure

2.3 Ellipsoid Modeling for Face Depth Picture

A representation equation of an ellipsoid in camera coordinate system is as follows:

$$x^2/a^2+y^2/b^2+{\left(z-c\right)}^2/c^2=1,$$

(4)

where a, b, c mean parameters of the ellipsoid and c means radius of the ellipsoid for the z-axis. Therefore, c can be approximated by the distance δ between depth values of the nose tip in the face and of a face boundary point. In this paper, the depth value of the face boundary point is set to a depth value of a left or right boundary point relative to the nose point. Therefore, δ is a difference between the depth values of nose and boundary points. Eq. (4) is modified to a representation for d as follows:

$$\begin{array}{l}\left(\frac{1}{{\delta }^2}\right)d{\left(X,Y\right)}^2+\frac{2}{\delta }d\left(X,Y\right)+\frac{x^2}{{\left(fa\right)}^2}+\frac{y^2}{{\left(fb\right)}^2}=0,\\ \delta =\max \left(|d_{nose}-d_l|,|d_{nose}-d_r|\right).\end{array}$$

(5)

where d_nose, d_l, d_r mean depth values of nose, left boundary point, and right bound point, respectively.

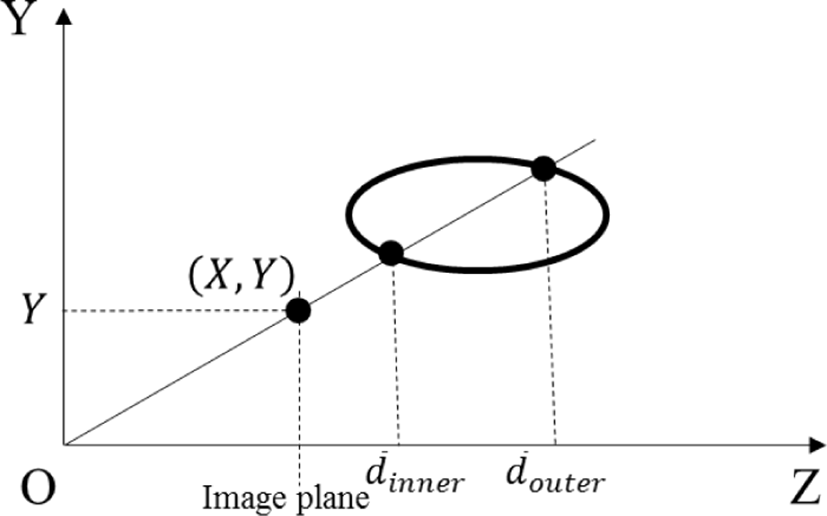
The depth value of the pixel located at (X, Y) with respect to the parameters a and b of the ellipsoid is solution of (5). At this time, 2 solutions of quadratic equations can be found as shown in Fig. 5. This means that 2 depth values can be predicted in the modeled ellipsoid. However, a surface of the face corresponds to the inner surface of the ellipsoid. Therefore, only the depth value of the inner surface is needed. The depth value can be predicted as follows:

$$\overline{d}\left(X,Y\right)=-c\left(1-\sqrt{1-4\left(X^2/a^2+Y^2/b^2\right)}\right).$$

(6)

where d̅ (X,Y) means a prediction depth value at position (X, Y).

Fig. 5. Predicted depth values in one ellipsoid.

Download Original Figure

Ellipsoid modeling is defined as finding the optimal parameters of the ellipsoid that minimize the prediction error. For ellipsoid modeling, the coordinates of the nose are set as the coordinate origin and the whole pixels of the face picture is subtracted from the depth pixel value of the nose. Then, the coordinates of the pixels substituted into Eq. (4) to obtain a following matrix equation:

$$\begin{array}{l}AR=B\\ A=\left[\begin{array}{cc}{x}_1^2& y_1^2\\ x_2^2& y_2^2\\ \mathrm{..}& \cdots \end{array}\right]B=\left[\begin{array}{c}-\left(\frac{d_1^2}{{\delta }^2}+\frac{2d_1}{\delta }\right)\\ -\left(\frac{d_2^2}{{\delta }^2}+\frac{2d_2}{\delta }\right)\\ \cdots \end{array}\right]\\ R=\left[\begin{array}{c}1/a^2\\ 1/b^2\end{array}\right].\end{array}$$

(7)

The ellipsoid parameters a and b are obtained by calculating R using the pseudo-inverse matrix of A by following equation:

$$\begin{array}{l}R=B{A}^{+}\\ A^{+}={\left(A^{\text{T}}A\right)}^{-1}{A}^T.\end{array}$$

(8)

The proposed ellipsoid modeling method is applied to the depth picture shown in Fig. 6. In Fig. 6, distributions of the depth value of the body in the depth image is 800-1100.

Fig. 6. Depth picture with body.

Download Original Figure

Fig. 7 (b)-(c) show pictures of ellipsoid modeling from Fig. 7 (a) and differences between the captured and predicted pictures, respectively. This means that a size of the face depth picture can be reduced through ellipsoid modeling.

Fig. 7. Prediction of face depth picture through ellipsoid modeling. (a) face depth picture, (b) predicted picture from ellipsoid modeling, and (c) Transmitted picture through ellipsoid modeling.

Download Original Figure

III. SIMULATION RESULTS

In this paper, we measured the prediction accuracy of the depth face image using ellipsoid modeling. The parameters for nose detection is as follows: M and N are set to 5 and 15, respectively. The focal length f is 585.6.

We use a dataset [16] of face depth pictures for the simulation as shown in Fig. 8. The dataset for simulation is captured by Kinect and it includes 810 pictures. The depth pictures in the dataset are captured for 9 face poses of 30 people. Each pose is captured 3 times. In simulation pictures, pixel values that is not part of the face are removed.

Fig. 8. Face pictures with various face poses for simulation.

Download Original Figure

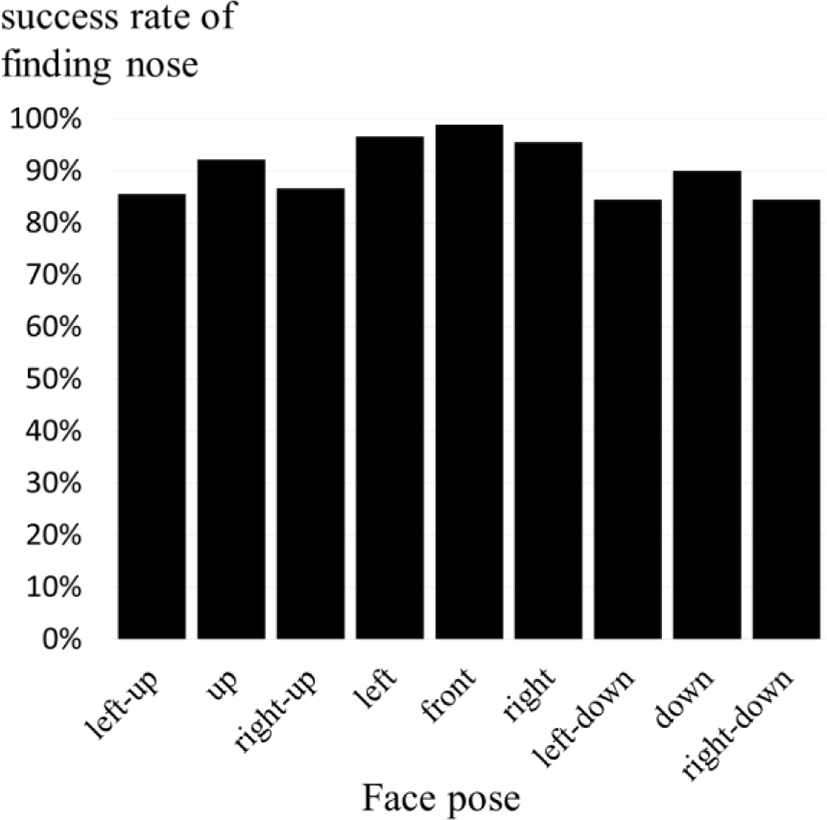
Measure nose detection accuracy. Because the depth face picture is accurately modeled through proposed method if a position of the nose is correctly found. Fig. 9 shows the success rate of finding the actual position of the nose. The nose is perfectly detected when the face pose is front, and the nose is detected with at least 85% accuracy even when the face pose is not front.

Fig. 9. Success rate of finding actual position of nose.

Download Original Figure

The predicted accuracies by ellipsoid modeling are measured for each pose of the face. For measuring predicted accuracies through proposed ellipsoid modeling, we measure MSEs(Mean of Square Errors) between original and predicted pictures as follows:

where w and h mean a width and a height of the picture, respectively, and I(X, Y) and P(X, Y) mean pixel values at position (X, Y) of original and predicted pictures. The results are shown in Table 1. As the results, an average of MSE is measured to 20.3, and MSE is smallest when the face pose is the front.

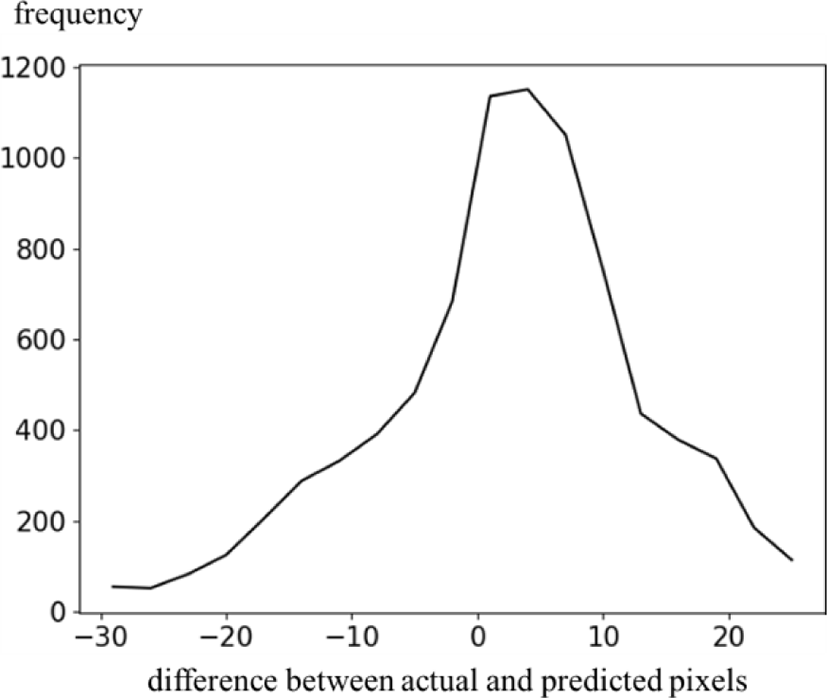
Fig. 10 shows a histogram of prediction errors between original and predicted pictures. In Fig. 10, an average of prediction errors is closed to 0, so this result shows that the proposed method effectively predicts the face depth pictures.

Fig. 10. Histogram for prediction errors.

Download Original Figure

An entropy power for the difference picture between original and predicted pictures is investigated to predict approximate coding efficiency. The entropy power is defined as the output of white noise with the same frequency of all signals in an environment. The entropy power N(x) for the inputs x is calculated as follows:

where f_i is the probability of a signal i. In the results shown by Table 2. Table 2 shows that the face depth picture can be effectively compressed by the proposed method.

IV. CONCLUSION

In this paper, we propose a method of predicting face picture through ellipsoid modeling to improve the transmission rates. The simulation results for the proposed method show that the face depth pictures can be efficiently predicted through the proposed method. In the face recognition methods using depth pictures that can accurately recognize the face without the influence of lighting, the proposed method is useful to quickly transmit the face depth pictures. The proposed method is expected to be applied to the field of identity recognition, which is recently increasing in importance.