I. INTRODUCTION
Mode matching technique is one of the most frequently used methods for formulating boundary values problem. The mode matching method has been described in detail by Itoh [1]. Mode matching technique has been applied to various fields such as the analysis of metal strip loaded dielectric antenna [2], a rigorous full wave analysis of microstrip via hole grounds [3], the analysis of a coaxial to stripline discontinuity [4], the analysis of axially slotted coaxial cable [5], and the analysis of metallic plates in radial waveguide [6], and the analysis of a cylindrical symmetric structure [7-8].
Electronic beam sees impedance when it transverses vacuum components which have different radius. The coupling impedance is often measured by a coaxial line method [9-10]. The idea of this method is that the field distribution of a relativistic electron beam in the vacuum chamber can be simulated by a coaxial TEM transmission line with a central wire. However the insertion of a central wire could change the field distribution. The motivation of this brief is to confirm the effect of the insertion of a central wire. In this brief, the effect of coaxial wire in the cylindrical cavity is analyzed using mode matching technique. The electric and magnetic fields in the coaxial cavity are formulated in the propagating resonant regions and then boundary conditions are applied to these fields. The condition of eigen value problem was derived. Numerical results for the eigen value problem agree well with MWS commercial software [11].
II. CYLINDRICAL CAVITY
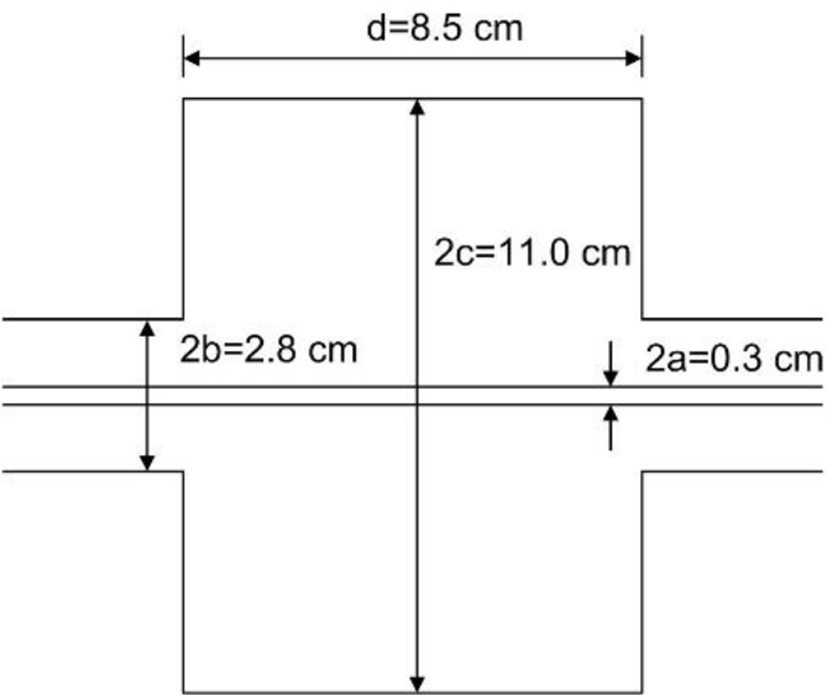
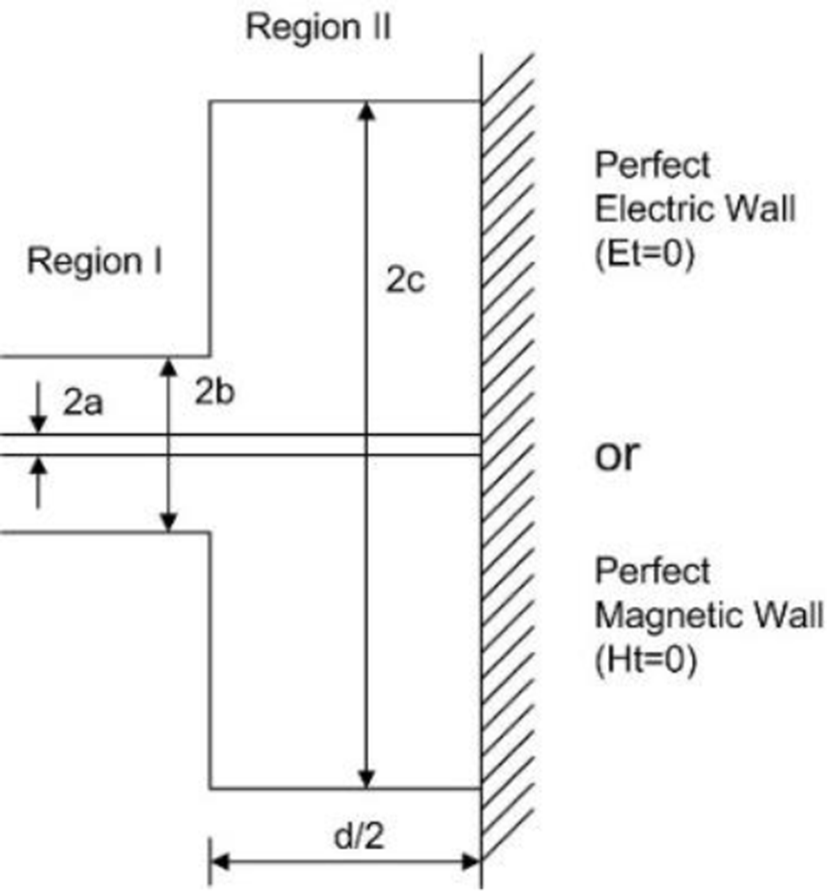
The structure under consideration, shown Fig. 1, consists of cylindrical beam port pipe with radius b, cylindrical cavity with radius c and length d, and cylindrical inner conductor with radius a. Due to the symmetry of structure about the cavity center plane, perfect electric wall (PEW) or perfect magnetic wall (PMW) can be placed at the plane to simplify the problems as Fig. 2.
The structure is divided in two regions: region (I), the propagation region and region (II), resonance region. The field in the regions (I) and (II) are represented by superposition of the modal functions in coaxial wire. We write down the tangential electric fields and magnetic fields as follows.
In region (I)
where w1n(ϱ) and w2n(ϱ) are modal functions in region I and region II with propagation constant β1n(ϱ) and β2n(ϱ) respectively, and
J0(kc 𝜌) and N0(kc 𝜌) are zero order Bessel function of the first and second kind and and refer to the derivative of J0(kc 𝜌) and N0(kc 𝜌) with respect to its argument repectively. It’s considered TEM and axial TM mode only, because of axial symmetric structure and TEM excitation. The modal functions satisfy the orthogonal relations defined by
where 𝛿mn is the Kronecker delta.
The boundary conditions that must be satisfied are
We have a set of equations by using the orthogonality of the normal function in (3a) and (3b)
where
By integrating directly on the boundary conditions
where
It is easier to handle the simultaneous equation in matrix and vector form
where is a matrix size N×N with generic element Mnm. The superscript T denotes the transpose operation, and , ,, , and are diagonal matrix.
From the equations (5a) – (5d), we have final equation
where
and the superscript -1 denotes the inverse operation.
The determinant of the coefficient matrix should be zero to have solutions. The resonant frequency is the frequency that makes the determinant of the coefficient equal zero.
The next case to be considered is modified pill box cavity with beam port which has no center conductor. Electric and magnetic fields equations become simpler forms and have no TEM components.
In region II
where
The next mathematical handling is the same as that of the coaxial cavity. We have the final equation
We can find resonant frequency that makes determinant of the matrix equal zero.
III. NUMERICAL RESULTS
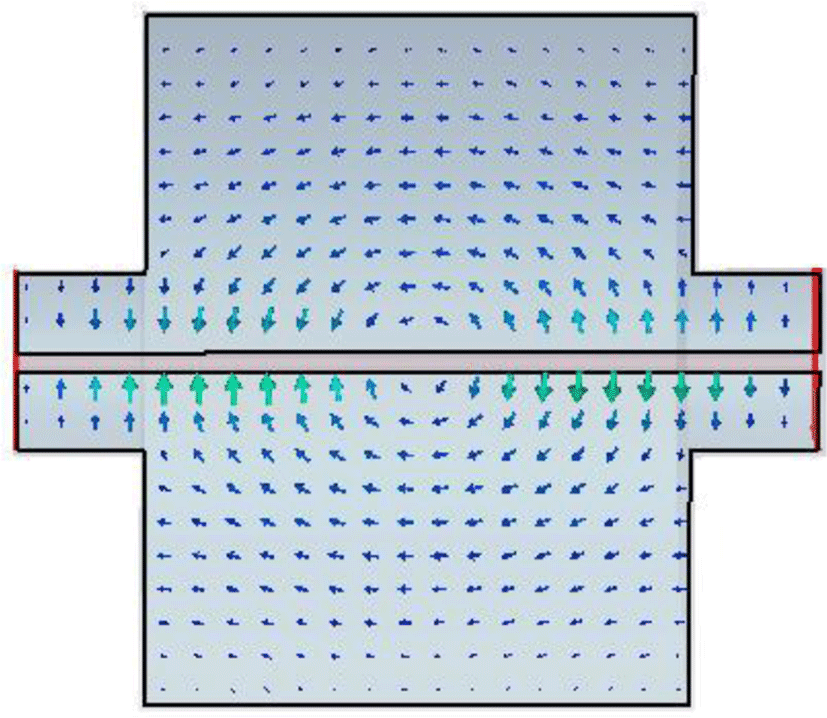
Resonant frequency of the coaxial cavity was calculated numerically by mode matching technique and simulated MWS commercial software. The calculated, simulated, and measurement results for a coaxial cavity are list in Table 1. Figure 3 shows the electric field of the dominant mode in the coaxial cavity.
| MWS Simulation | Mode Matching Technique Calculation | Measurement results | |
|---|---|---|---|
| Dominant Resonant Frequency | 2.540 GHz | 2.545 GHz | 2.543 GHz |
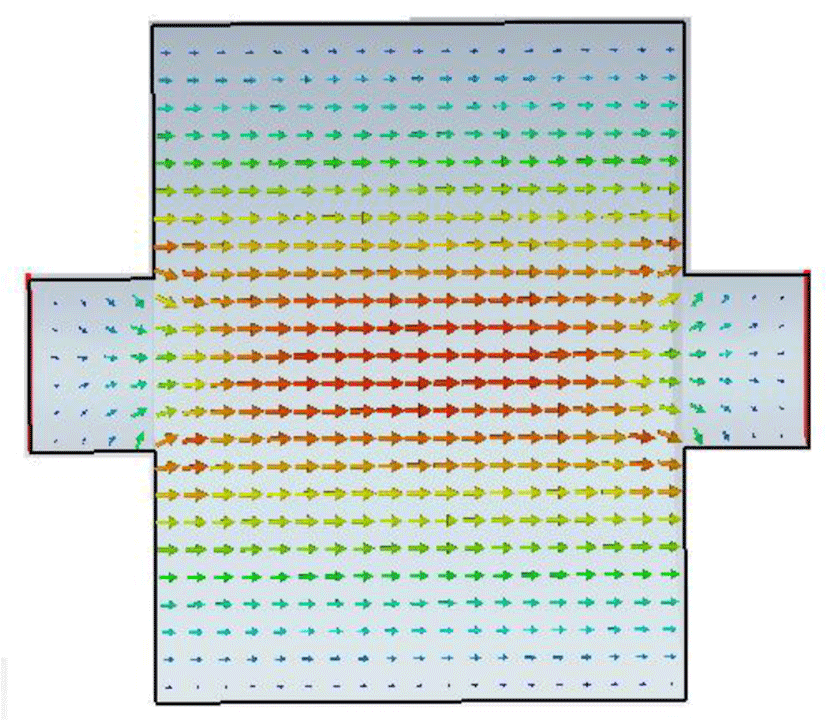
The calculated and simulated results for a modified pill box cavity are list in Table 2. Figure 4 shows the electric field of the dominant mode in the modified pill box cavity. Table 2 and 3 shows that the insertion of the coaxial wire increases the resonant frequency of the fundamental mode. This results mean that coaxial line method of the coupling impedance is not adequate for a cylindrical cavity.
| MWS Simulation | Mode Matching Technique Calculation | |
|---|---|---|
| Dominant Resonant Frequency | 2.098 GHz | 2.086 GHz |
IV. CONCLUSION
In this brief, the mode matching technique is applied to the coaxial cavity and the modified pill box cavity. The results of mode matching technique and the simulation agree well. The proposed procedure can be applied to coaxial structure. The results show that the insertion of the coaxial wire increase the resonant frequency. The coaxial line method of the coupling impedance is not adequate for a cylindrical cavity. The proposed formulation can be used cylindrical symmetry structures such as a coaxial line filters and coaxial transitions by solving transmission characteristics.