I. INTRODUCTION
Soil Moisture Content (SMC) is one of the key factors used to estimate direct surface runoff for flood forecasting, because the state of soil moisture at storm initiation has a large effect on the overall runoff magnitude [1-4]. Depending on the soil texture and its surface condition, the assumed SMC could lead to a considerable runoff error larger than that arising from the rainfall estimates [5]. The SCS-CN method was developed by the United States Department of Agriculture (USDA) Soil Conservation Service in 1954 and is now referred to as the Natural Resource Conservation (NRCS) SCS-CN method [6-9]. The SCS-CN method has a parameter, the curve number (CN), representing SMC using a quantitative numerical value ranging from 30 to 100.In general, CN values are based on land use and soil type mappings. The land-use map reflects the vegetative cover conditions on the surface and the soils map supports assignment of hydrologic condition classified as A (well-drained soils with low runoff potential) to D (low infiltration with high runoff potential) [10].
However, these studies mainly focused on long-term hydrologic simulations where S is allowed to vary at the daily or longer time scale. For example, the previous studies used the average monthly lake evaporation as a climatic index and a depletion coefficient to consider a decrease of SMC.
In this study, a potential maximum soil moisture retention curve (S-curve) is developed to estimate a time-variable SMC at hourly time-scales in order to improve continuous flood forecasting. For this purpose, a change of S for complex storm events and Inter-Event Time Duration (IETD) between independent storm events has been developed. This study has been applied for the Napa River basin, California. The streamflow gage at St Helena (USGS station #11456000), located in the upper reaches of the basin, is used as the control gage site. 16 rainfall events from 2011 to 2012 are used for estimating the event-based SCS S-curve.
S is the total depth of moisture that could be stored in the soil column, including tension water adhering to the soil matrix and free water drainable by gravity. Also, S represents a change of SMC generally used to estimate a direct runoff in hydrologic modeling. Fig. 1 shows a physical soil layer, soil profile and a concept of soil moisture accounting to understand the meaning of S and SMC through the volumetric terms such as air, water, void and the moisture contents.
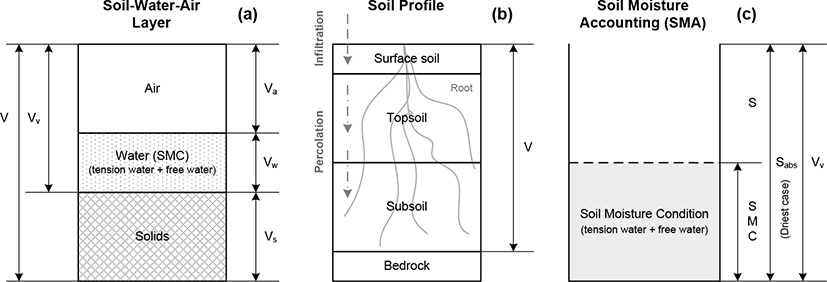
Basically, the S depends on the volume of the soil-water-air layer. In Fig. 1 (a), the soil could be classified among solids, water and air. Solid indicates the total volume of the soil particles and water consists of current tension water and free water arising from previous precipitation. In general, these two water volumes comprise the SMC. Air is a void space which can hold SMC through infiltration and percolation. Both layers, air and water, are the potential SMC storage. The total volume of voids is shown by Eq. (1).
Where, Va is the volume of air, and Vw is the volume of water. The sum of air and water represents as the total volume of voids, Vv. V in Fig. 1 is the total volume.
In Fig. 1 (b) soils are divided into surface soil, topsoil, subsoil and bedrock. Surface soil is associated with land-use as it relates to infiltration due to impervious surfaces, for example. Topsoil and subsoil establish the percolation rate according to soil texture. The total volume of voids is comprised as the sum of the soil-water-air layer in Fig. 1 (a). Based on the soil profile, infiltration and percolation rates could differ, and the percolation rates from topsoil to subsoil could differ as rainfall moves further downward.
For soil moisture accounting (Fig. 1 (c)), the volume of voids, Vv, is the sum of S and current SMC. If the soil is very dry, S is the absolute potential maximum retention, Sabs (or maximum S). A representative study by Williams and LaSeur [11] developed an approach for estimating current SMC using a relationship between the absolute potential maximum retention and potential maximum retention expressed as:
where SMC consists of tension water and free water, which depend on antecedent precipitation. Also, S is dependent on the variation of SMC.
The SCS-CN method is based on a water balance equation and two fundamental hypotheses [4]. The first, water balance assumption equates the actual amount of direct surface runoff (Q) to the total rainfall (P) and the ratio of the amount of actual infiltration (F) to the amount of S (Eqns 3 and 4). The second assumption relates the initial abstraction (Ia) to S (Eqn5). Thus, the SCS-CN method consists of
(a) Water balance equation:
(b) Ratio hypothesis:
(c) hypothesis:
Here, ■ is the initial abstraction coefficient. Historically, it is 0.2. Physically this means that for a given storm, 20% of S is the initial abstraction before runoff begins. However, Hawkins et al. (2002) found that the ratio of Ia to S varies widely, and they suggested that the ratio be 0.05 rather than 0.20.
The NRCS runoff curve number method is based on the following basic form to calculate direct runoff from a rainfall depth.
Eq. (6) (SCS, 1985) becomes
S is expressed in terms of the dimensionless SCS-CN through the relationship taking values from 0, when , to 100, when S → ∞, to 100, when S = 0.
This definition was originally applied to the English metric system (with S in inches). In the SI units (with S in mm) the following definition should be used:
II. APPLICATION DATA
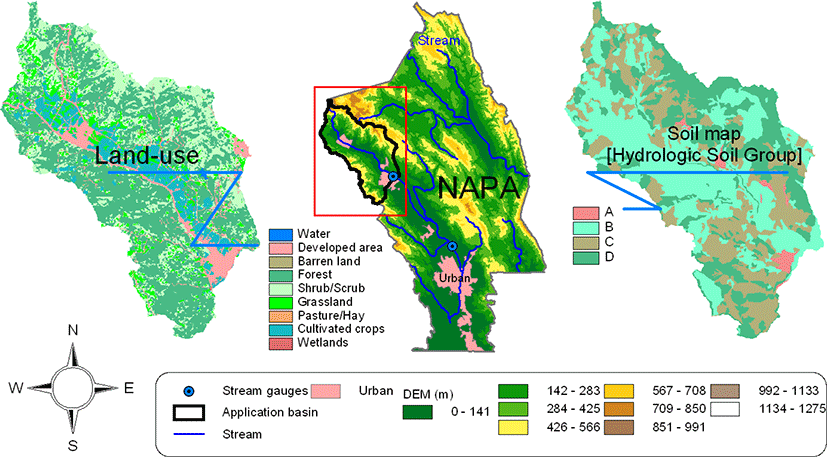
The Napa River basin in Napa County, CA, is used as application watershed. This basin has two continuous flow gages managed by the U. S. Geological Survey (USGS); the gage at St. Helena, Napa County, CA, (USGS 11456000) station was the primary site for this study. The combined Russian-Napa Rivers have been the focus for assessment of distributed hydrologic modeling [12].
As a consequence, we have compiled a large archive of watershed and precipitation data useful for this study. Fig. 2 shows the Napa watershed including the land-use and the soil map. The drainage area is 204.8 km2 (79.3 mi2). Annual average precipitation is 508 mm to 685 mm of which 80% occurs mainly during the rainy season from November to March. During the rainy season there is a higher likelihood for multiple rainfall events within a few days.
Table 1 lists the fraction (%) of area depending on the land-use type and the hydrologic soil group in the basin (Fig. 2). The sum of forest and grassland/herbaceous exceeds 65%, followed by cultivated crops (9.9%), pasture/hay (8.4%), and shrub/scrub (7.1%). Based on the hydrologic soil group (HSG), the drainage capability is relatively low as the well-drained HSG A area is only 1.5%, and there are large areas of poorly drained HSG C (28.6%) and D(29.5%) soils. The NRCS cover type influences the initial SCS-CN mapping. Table 1 shows the Min./Max. SCS-CNs associated with the NRCS cover types. For example, for HSG C the CN can range from 65 to 88.
As part of on-going modeling of the Russian-Napa watersheds [12] we have collected gridded precipitation fields useful for hydrologic modeling, including data from the Multi-Radar/Multi-Sensor (MRMS) system[13]. MRMS is a system with automated algorithms that integrate data streams from multiple radars, surface and upper air observations, lightning detection systems, and satellite and forecast models.
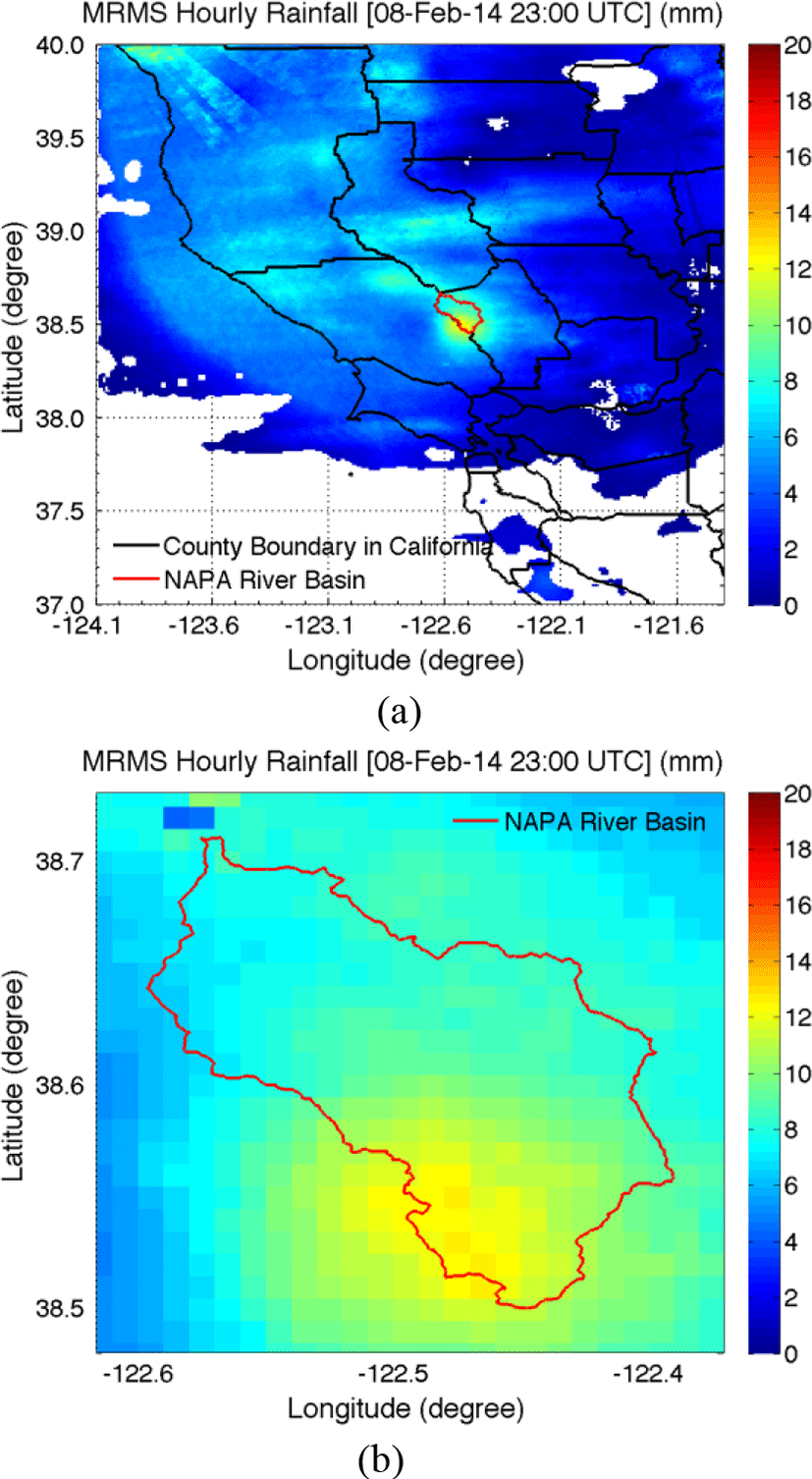
The MRMS quantitative precipitation estimation (QPE) products can be classified based on the use of radars, the use of ground gauges and a bias correction method. For the purposes of this study, gridded precipitation fields at a spatial resolution of 1.0 km and temporal resolution of1 hour were used. Moreover, the MRMS QPE was generated using the Vertical-Profile-of-Reflectivity (VPR) and Mean Field Bias (MFB) correction [14-15]. Fig. 3 shows (a) a sample MRMS hourly rainfall map in Northern California and (b) the same sample MRMS hourly rainfall map for the application basin.
III. APPICATION of S-CURVE METHOD and ITS RESULT
An S-curve is a relationship between ΔS and IETD to represent a time-variable SMC at hourly time-scales in order to improve continuous flood forecasting. A method to derive the S-curve is explained as follows:
(a) Select complex storm events having significant multiple rainfalls within 72 hours with shorter IETD. In this study, 72 hours is assumed as the maximum IETD to classify an independent rainfall event, so that we have looked for ΔS within 3 days.
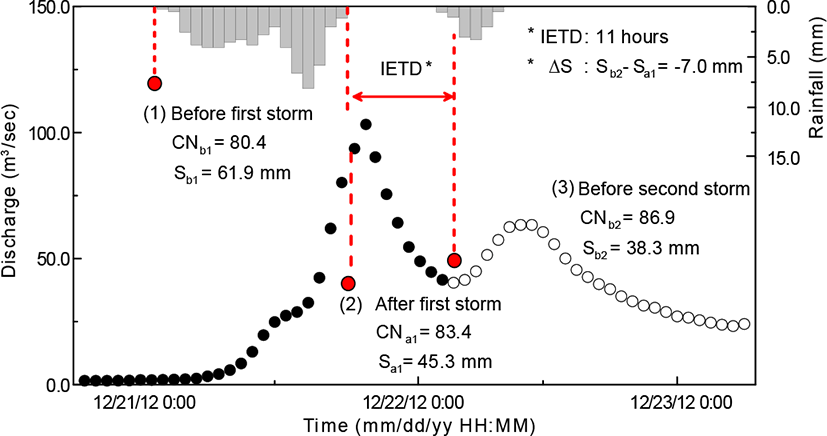
(b) Separate the runoff hydrographs as observed at the USGS gage. In the hydrograph separation process, the direct runoff is calculated to estimate an event-based SCS-CN for each storm pulse; this study used the N-Day method and the cubic spline interpolation method. In addition, Fig. 4 shows the definition of S during three time periods (Sb1, Sa1 andSb2). Sb1, Sa1&Sb2 are associated with the first and second rainfall pulses, respectively. Also, Sa1 andSb2 are associated with the inter-event percolation of soil water downward to the lower layer.
(c) Estimate the CN for each rainfall pulse. To estimate the CN, we used the initial CN map based on the land-use and soil maps. The initial CN was changed incrementally by 1.0 % to determine the best appropriate event-based CN for each rainfall pulse.
(d) To derive the S-curve, three S values for three time steps are required. The first S value, Sb1, is for the first storm pulse. Sb1can be estimated through the process (c) as above. The second S value, Sa1, is for the time after cessation of the first rainfall pulse. The third S value, Sb2, is for the second rainfall pulse. Sb2can be estimated using the same process to estimate Sb1.
(e) Calculate the IETD between two rainfall storms. IETD is defined as a time period enabling the recovery of S through the downward movement of SMC and evaporation. IETD is calculated considering the time duration from the end of first rainfall storm to the first response of hydrograph arising from second rainfall storm (Fig. 4). This study assumes that any small rainfall amounts (less than 0.5 mm) occurring during the IETD has no effect on the volume of runoff flow and on the recovery of S.
(f) Derive the relationship between a change of S values and the IETD. We calculate the change of S values using the difference of Sa1and Sb2. It indicates the change of two S values during the IETD enabling S to recover the volume to store SMC. Thus, we can derive the relationship between the change in S and the IETD.
Based on the process explained as above, this study derived the relationship between the change of S values and the IETDs using 16 rainfall storm events.
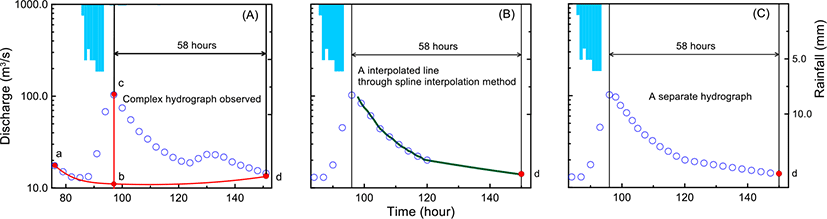
Hydrograph separation of multiple discharge peaks arising from a multi-pulse rainfall event requires calculation of direct runoff for each pulse. To separate the multiple hydrograph into its components (i.e. base and direct flows) we used two methods, N-day and spline interpolation method. The N-day method estimates the duration between a time-to-peak and the runoff flow recession at the end of a hydrograph; this is an adaptation of an equation like Eq. (9).
For the Napa River basin N-days is approximately 2.4 days (58 hours), when substituting the drainage area 79.3 mi2.
Here, N is the number of days runoff ceases after a storm, and A is the drainage area of the application basin (mi2).
Fig. 5 shows the process to separate a multiple peak hydrograph into its pulse components, described as follows: (1) Estimate the duration from a time to peak to the end time of runoff using N-Day method as in Fig. 5 (a). (2) Use the spline interpolation method to estimate the pulse discharges on the regression limb, as in Fig. 5(b). When applying the interpolation method, this study used the discharges for the regression limb and the end time of runoff flow from the N-Day method. Finally, the separated hydrograph is shown in Fig. 5 (C). A similar process is done for the remaining peaks.
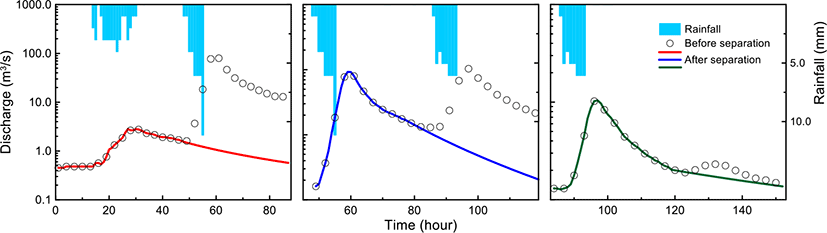
Fig. 6 shows the results of the hydrograph separation for the multi-pulse rainfall storms occurring between14 to 18 Feb. 2011. During the storm, three rainfall pulses occurred sequentially, and the overall hydrograph is separated using the technique described above (Fig. 6).
A gridded CN for each storm event is estimated using an initial gridded CN map and a simplified optimization method as described at section 3.3. The initial gridded CN map was estimated from Table 2 with both minimum and maximum CN values to determine the difference of CNs depending on NRCS cover types. Fig. 7 shows the result of the initial gridded CN map and its corresponding S values. As shown in Fig. 7, the areal mean CN using the minimum values is 67; the maximum mean CN value is 81. In case of S, the maximum S is twice the minimum S because CN-S relationship is non-linear. Areal mean S using minimum CN is 134.3 mm and the areal mean S using maximum CN is 61.4 mm. These S values indicate the amount of SMC in which soil column could hold at any particular time.
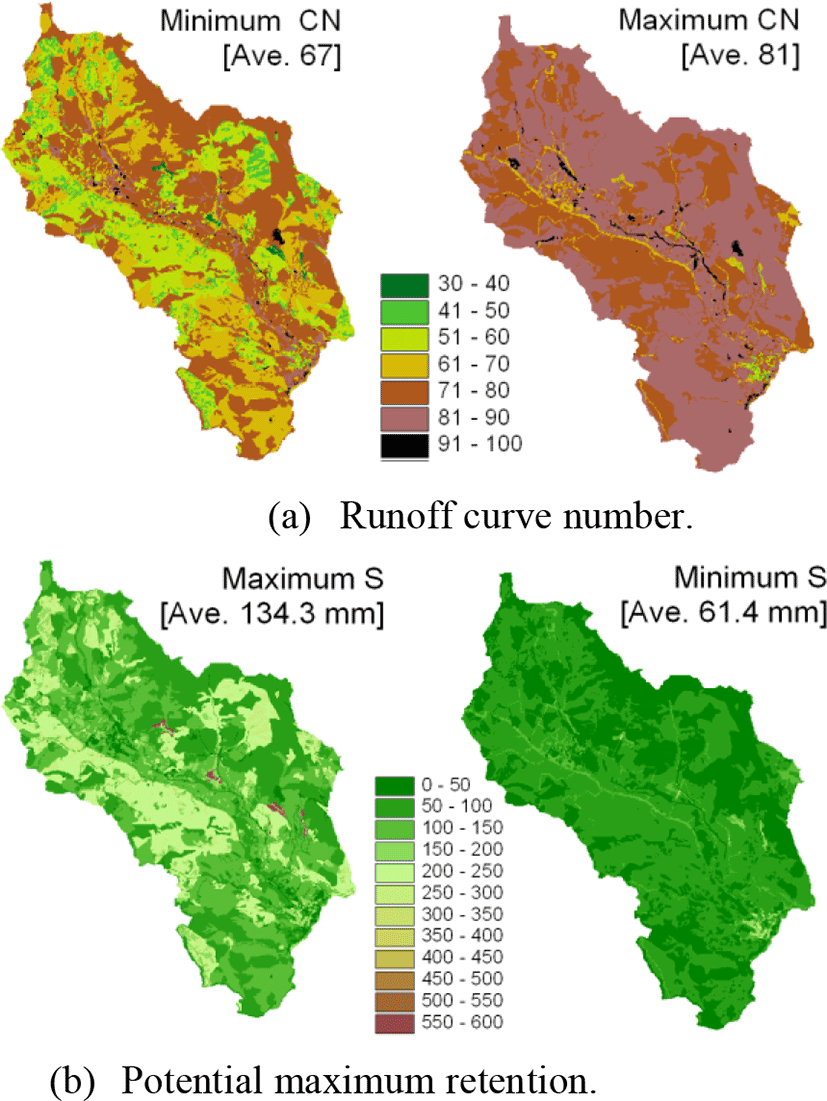
To estimate a gridded CN for each storm event, we used the initial gridded CN with minimum values from Table 1. The main reason for using the minimum values is that the CN values were not optimized by using initial gridded maximum CN. The non-optimized values resulted in a large difference between the volumes of a direct runoff from observed discharge and direct runoff amount. There has no difference when using minimum values for initial gridded CN map.
The resulting S values (Sb1, Sa1, Sb2 and a change of S) are tabulated in Table 2. This table also lists the total rainfall, direct runoff, estimated CNs and IETD for deriving the S-curve for each event. In Table 2, the first S value, Sb1, is estimated at the time just before the onset of the first rainfall. The second S value, Sa1, is representative of the time just after the first rainfall period ends. The third S value, Sb2, represents the first response of the second hydrograph arising from the second rainfall period. According to Table 2, the range of IETD for all 16 events is from 10 to 66 hours and the range of change of S is from −26.36 to +27.84 mm.
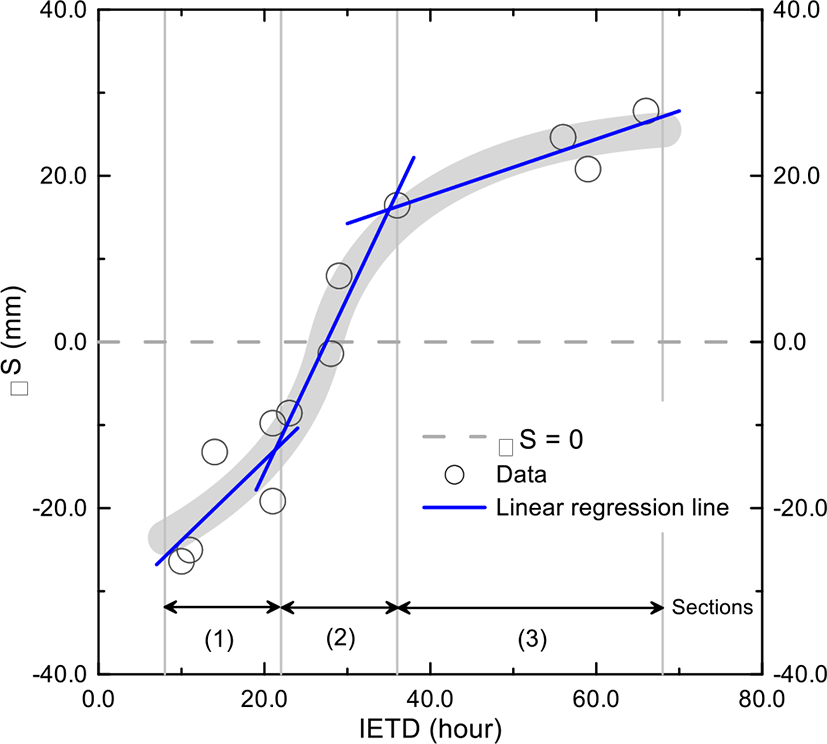
The S-curve is derived from the relationship between IETD and the change of S values as shown in Fig. 8. The S-curve is divided into three sections according to the recovery rate (mm/hr) of S. Root Mean Square Error (RMSE) is used as a criterion to decide a more apt linear regression line to estimate the recovery rate in each section.
For the three sections, (1) the first section is in the range 10 to 21 hours and exhibits a gradually recovering S (0.97 mm/hr or 23.28 mm/day), (2) the second section is in the range 21 to 36 hours and exhibits a steeply recovering S (2.11 mm/hr or 50.64 mm/day), and (3) the third section is in the range 36 to 66 hours and exhibits a gradually decreasing recovery (0.34 mm/hr or 8.16 mm/day).
During the recovery of S within a few days, other influencing factors include evaporation and the downward movement of SMC consisting of free water and tension water. Depending on the contribution of these factors in each section, the recovery rate could be different. Therefore, we conceptually analyzed the difference of S recovery phenomenon with these factors according to three sections and described the limitation of SCS-CN method because it regards a soil column as a single layer in accounting for the total value of S as described below.
Curve derived for the NAPA River basin, based on 16 rainfall events. S-curve sections 1, 2, and 3 represent the gradually recovering S section, the rapid recovery of S section and the gradually decreasing recovery section, respectively.
IV. CONCLUSION
This study developed a potential maximum retention curve (S-curve) to estimate a time-variable SMC at hourly time-scales in order to improve continuous flood forecasting. The S-curve was based on a change of S for storm events with multiple peak hydrographs and an IETD criterion to identify independent storm events as defined in this study. The data were obtained for the Napa River basin, California and 16 rainfall events from 2011 to 2012 were used in estimating the event-based S. The salient results of the study include:
The S-curve is derived from the relationship between IETD and a change of S values, and is divided into three sections according to the recovery rate (mm/hr) of S.
For the three sections, (1) represents the period of 10-21 hours and involves a gradually recovering S (0.97 mm/hr or 23.28 mm/day), (2) represents the period 21-36 hours and involves a period of steeply recovering S (2.11 mm/hr or 50.64 mm/day), and (3) is for the period36-66 hours and involves a gradually decreasing S recovery (0.34 mm/hr or 8.16 mm/day).
The first section has the retardation effect because SMC in upper soil zone is not yet saturated and not draining to lower zone. This results in temporary soil saturation in upper zone. The main reason for the flow retardation is the difference of movement rates between infiltration for the upper zone and percolation for the lower zone. When the infiltration rate is faster than percolation rate, the boundary layer between upper zone and lower zone could develop a temporary stagnant water layer when the retardation effect occurs. When the upper zone is saturated, it appears as if the total SMC is increased without additional rainfall during IETD, even though actual total SMC is decreased.
The second S-curve section involves rapid recovery of S. It is the fastest rate among three sections because the movement of SMC to lower soil layers is occurring. The third section has a gradually decreasing S recovery rate. In this section, the movement of SMC is provisionally complete, and evaporation and outflow through interflow and subsurface drainage are dominant factors to the recovery of S. Thus, the S recovery rate is the slowest among three sections. The recovery rate of this section converges on a constant value close to zero.
Based on these results, the S-curve could be used to determine hourly time-series of SMC. Also, this technique could be used to overcome the limitation of the SCS-CN methodology which regards the soil column as a single layer in accounting for the total value of S using S-curves in terms of continuous applicability for a long-term simulation. In addition, the S-curve method could provide a simple indicator of the state of SMC which could help for flood forecasting during a complex storm event with multiple rainfall pulses and hydrograph peaks.