I. INTRODUCTION
Information regarding sports videos has always been coveted. Due to the nature of sports and the sheer following behind it the popularity of statistical analysis of sports videos is highly desired. A need for a tracker of players that can work on several sports and robust to handle different situations such as occluded players, low-lit conditions and to be able to handle fast paced sports with several awkward positions of players is that might even work in a live scenario (broadcast sports such as the NBA or FIFA) is extremely in demand. This paper is an attempt to solve this issue by providing an architecture by which one could create such an efficient tracker that could track players in the live scenario and also be robust in nature to handle all the aforementioned situations. A simple yet moderately effective approach already existing was to identify the background of the field and use background subtraction to track the players by calculating the absolute difference, applying erosion and dilution and obtaining the contours. Such a system works when the object is singular with a clear background. However our situation is much more difficult. Issues arose when players overlapped amongst each other and many false positives were detected. Also such a tracker could not applied to situations where the whole court was not in view: such as the NBA basketball videos. However, this tracker also fails to track broadcast sports. The next attempt was to use a Meanshift tracker [4] to track players in the our sports videos, but this attempt was partially successful. The Meanshift Tracker is fast and works well, however when players get occluded, or when similar colors in the background appear the tracker fails to identify the next position. Hence, we need a tracker that could predict the next location and can handle occluded situations. Also this tracker cannot identify players in a broadcast scenario. Of note, certain sports videos such as tennis and badminton were tracked using this method with accurate results. This is because the number of players in these sports are 2 players and they rarely get occluded.
Therefore we identified certain challenges: The first challenge was to be able to track players in a broadcast scenario. We used a Convolutional Neural Network by feeding it images of court view shots and non-court view shots such as advertisements, etc. The second issue was detecting the players even in occluded conditions with a high accuracy. We use machine learning pre-trained models that can detect humans that has been trained on extremely large datasets and provide accurate results for low-resolution images seemed like a way to go. Such models are available for the public domain. The final issue was to be
II. RELATED WORK
Object Detection and Tracking is a vast area and many strategies and methodologies are tried to achieve results. In order to track players several papers have defined efficient tracking algorithms and methodologies such as the KCF Tracker [3], and the Mean-shift tracker[4]. The KCF Tracker is a kernel algorithm and the mean-shift algorithm is used for Mean-Shift Tracker. These tracker efficiently track objects, tracking them at high fps, however they fail tracking when players are small in size with respect to the overall region or moving at relatively high speeds. A recent approach that is interesting lead to object detection in complex environments using background subtraction for fast tracking[8]. However, important to note is all these trackers lack a global view of the scene and thus usually fail to track players when occlusion occurs. Kalman Filter was also used to track objects even in occluded situations at high speeds with predictive capabilities. Our papers borrows ideas from [9] and the ability of the Kalman filter to predict new positions based on past information. Tracking objects in this way alone is not sufficient for our use-case because of the aforementioned problems. Therefore a need arose to find a different method to detect players. With the rise of neural nets in recent times we employ a pre-trained model derived from [5] that uses resnet [2] and faster r-cnn [13] to deliver incredible results in the field of image object identification. We use this information to create model architecture that can dynamically detect and track players in most conditions. Statistical analysis of players is done with simple euclidean geometry. Our proposed model incorporates these ideas into a single flow and tries a different approach to track players and map them to a top-down view for statistical analysis. Meanshift Tracking is done by using the mean-shift algorithm. The meanshift algorithm is an efficient approach to tracking objects whose appearance is defined by histograms. The meanshift algorithm moves our window to the new location with maximum density. A confidence map is created in the image and based on the color histogram of our tracking object that was obtained in the previous image, we use mean shift to find the peak of the confidence map near the region of the object’s old position. The peak will point us to the new location and hence we track this mean. This can be used to track not only color space but any system that contains histograms.
The Kalman filter model assumes that the state of a system at a time t evolved from the prior state at time t − 1 according to the equation
where xt is the state vector containing the terms of interest for the system (e.g., position, velocity, heading) at time t, Ft is the state transition matrix which applies the effect of each system state parameter at time t − 1 on the system state at time t (e.g., the position and velocity at time t − 1 both affect the position at time t). ut is the vector containing any control inputs (steering angle, throttle setting, braking force). Bt is the control input matrix which applies the effect of each control input parameter in the vector ut on the state vector. wt is the vector containing the process noise terms for each parameter in the state vector. The process noise is assumed to be drawn from a zero mean multivariate normal distribution given a covariance matrix. Measurements of the system can also be performed, according to the model
where zt is the vector of measurements, Ht is the transformation matrix that maps the state vector parameters into the measurement domain, vt is the vector containing the measurement noise terms for each observation in the measurement vector. This gives us the prediction of the new state which can be used to give the next most likely position of the player. Any two images of the same planar surface in space are related by a homography. Homography can be used to map different planar structures amongst each other if we assume them to be the same or similar. Once camera rotation and translation have been extracted from an estimated homography matrix, this information may be used for navigation or even map points from one perspective to another.
The four main building blocks to define a basic convolutional neural network are Input Layer, Convolutional Layer, Pooling Layer, Output Layer. The input layer consists of the image as an n x n dimensional array. The convolution layer is the main building block of a convolutional neural network. The convolution layer comprises of a set of independent filters. Each filter is independently convolved with the image to obtain the corresponding feature maps. The pooling layers function is to progressively reduce the spatial size of the representation to reduce the amount of parameters and computation in the network. Pooling layer operates on each feature map independently. The output layer is fully connected to the previous layer and predicts the output of the system. The Network is trained with images and the weights and biases of the connections are updated by using backpropagation.
III. PROPOSED MODEL ARCHITECTURE
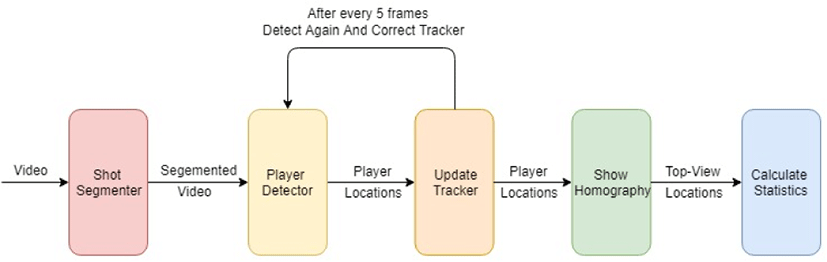
In order to achieve our desired results we have come up with a model architecture to track players in broadcast sports as shown in Figure 1.
For each frame we first send it through the shot-segmenter module in order to determine whether the frame is a view of the game or some other image. If negative we discard the frame and take the next frame. We want to only display game-view images in our resultant video and hence we proceed only if the result is positive. We then send the frame through a pre-trained object detection neural network to identify the bounding boxes of players. Once we get the bounding boxes of the players we track the players using an appropriate tracker to keep track of the player and predict his next position [5]. After this we map the player’s location to the corresponding point on the homographic top view of the court or field. Then based on the dimensions of the field we can calculate the distance travelled by the player.
During certain game videos such as the NBA videos, the videos have advertisements, close up views of players and other frames in the video which are undesirable. In order to eliminate such shots and leave only the game video containing the players on the court we have developed a convolutional neural network to classify whether a given image is court-view or not. The CNN has 6 layers and takes (64,128) size images using the Adam optimizer. Actual size images are 854 x 480 pixels in dimensions and so we resize our image to 64 x 128 pixels and send it into the CNN.
In order to detect the player locations we need to be able to identify humans in pictures. To do this we use a pre-trained model to identify bounding boxes of human-like figures in our frame. The way we achieve this is two-fold. First our image is of very high resolution: 4450 x 2000 pixels. The pre-trained model does not give accurate results as it scales the images to 300x300 pixels. Therefore we take our image and segment it into many images (around 150) and send it to the model to identify the players. The second step is to eliminate overlapping images and false positives. This can be done by comparing area of the bounding box, ratio of the bounding box and distance between the bounding boxes and the rgb histograms of the boxes. The players are then successfully identified. The last step in this process is to select the model for detecting player locations.
After detecting the players we need to identify the teams in which they belong to. In order to identify which team the player belongs to we use RGB Histograms. Whatever the game we take instances of players of both teams. And then we use those pre-computed RGB Histograms of players and compare them to the histogram of our current bounding box. The closest result is given as the corresponding team [10]. As the colors are usually far apart this usually gives high accuracy. If the area has large differences to both the pre-computed histograms then we can even discard this bounding box before proceeding. This occurs for example if the referee is identified or if a player in the crowd is identified.
For tracking players we use a two-step process. Using the pre-trained model to identify the locations of the players for every frame takes too long for tracking and hence the need arises to use a tracker. In order to predict the next location of the player we use Kalman Filter based on the last known location and last known velocity [6]. After a set number of fixed frames we use the ML model to find the correct current location and update our tracker accordingly. Therefore the tracker tracks the player for some time and is fast and after the predetermined fixed number of frames, the tracker is corrected based on the correct location of the player. The proposed algorithm for detecting players is given in Algorithm 1.
The matchBox function arises as a need to match new and old player locations. Essentially, in order to update the tracker using the correct location we need to know which player location (obtained from the ML model) corresponds to which player (from the tracker). This is done using our matching algorithm which is essentially to find the nearest box to the given box and match it. Our matching algorithm takes all the bounding boxes and checks within a pixel radius for bounding boxes (compares only new bounding boxes obtained from the ML Model). This pixel radius is defined as product of the number of frames and a constant in order to map the bounding box within an appropriate radius. If there are multiple bounding boxes near that corresponding player we match it with the one with nearest distance. After the matching of one box is complete we eliminate that box from the list so as to avoid repetitions. Two cases arise in this situation. If the number of new boxes are equal to the number of previous boxes then the players are matches as a bijections. However, if the number of new boxes are more than the number of previously identified boxes then the extra boxes are added to the list of tracked players (assuming the boxes represent players based on their histograms). If the number of new boxes are less than the number of previous boxes we pass on the missing box as is. This is because there may be a future frame where the player is identified again and then this will help in resuming his movement and getting consistent statistic results.
After tracking we need to map each player location to the top down view of the field of the corresponding sport. In Figure 2a we have the panoramic football field containing the players. In Figure 2b we have the top down view of a football field. In order to map the locations we compute the homography between the two images by mapping points around the boundary of the two images. However as the first frame is a panoramic view this poses a challenge. We used a unique method to calculate the homography.

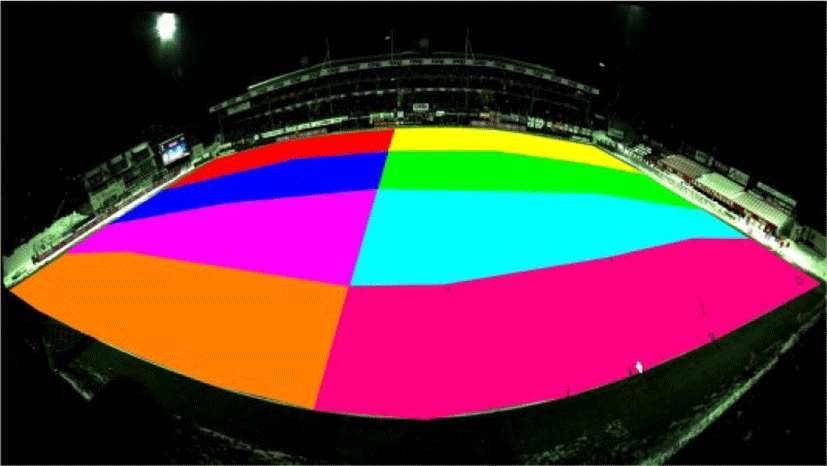
We partitioned the image into 8 different areas each represented by a color as shown in Figure 3. Each of these individual parts are mapped to the corresponding area in the topview image. We calculate the individual homography transition matrices for all 8 divisions and assign it to the corresponding color. Now in order to map the player we find the foot position of the player and find which color region this position belongs to by identifying the pixel color of the corresponding pixel in Figure 3. Hence we find the corresponding homography matrix and transform the point to our top view image.
Finally, we calculate the distance travelled by the players and the trail of the player on the top-view of the field. The distance is stored as a separate variable for each player. Between each frame we find the player locations calculate the Euclidean distance between them in pixels. We then use the aspect ratio of the top down view with respect to the size of an actual football field in order to calculate the distance travelled by each player by multiplying this constant with the distance calculated. In order to find the trail of the player we just define a number of frames where we store the players previous frame location and plot all of those points on the top-view image. After we exceed this limit we delete the oldest known location and append the newest.
IV. EXPERIMENTS
In this section, we present the dataset information and the experimental details used in this work.
The dataset consists of 1000 video clips of NHL games. Each video clip consists of 50 frames. The resolution of each frame is 720 × 576. The video frames are labeled into two classes i.e. fight and non-fight. Each video clip is further divided into two consecutive parts consisting of 25 frames each to increase the number of training samples. 70% of the total data is used to train the networks, 10% for validation and the left 20% is used for testing the trained models. The training and validation clips are randomly picked from the dataset. The data is randomly shuffled after each epoch for robust training and testing.
In this section, we discuss the different datasets we used to implement and test the proposed model architecture. Shot-Segmenter Dataset In order to train our shot segmenter we created our own dataset from 5 full-length NBA videos. Each video was approximately 90 minutes long. In order to get more diversified training data we took only a single frame for every five frames. We got around 12000 frames per video and around 3000 negative images and 9000 positive image. We discarded 6000 random positive images as we wanted equal number of positive and negative matches for good results. Therefore, after all 5 videos we ended up with a total of 15000 positive image results and 15000 negative image results. This was fed into a Convolutional Neural Network to create our shot-segmenter. Football Dataset Here we required a panoramic view of the entire football field. This was obtained by using the dataset provided by [12]. They had 3 stable wide angle digital cameras setup on a football field with an actual match. The total video available is around 40 minutes of resolution 4450 x 2000 pixels. The video also contains the actual positions of the players in reference to the figure shown below. The soccer pitch is 105 x 68 m wide and valid in-field values for x and y are in the range of 0 ≤ x ≤ 105 and 0 ≤ y ≤ 68 where x,y represent player positions. Other Datasets, Other live videos were full length videos of various sports found on the internet. As our system was designed to track even in broadcast sports by identifying the court frames we have used direct video feed from multiple archived games. For example, for basketball tracking we have used Utah Jazz vs Oklahoma City Thunder match found by the YouTube research dataset provided by Google [1].
In this section we discuss the implementations of various parts of our model architecture. Shot-Segmenter We trained our shot-segmenter model for 50 epochs using adam-optimizer with a learning rate of 0.0002. Then we take full length basketball videos and feed it into our shot-segmenter to get isolated court shots. After this video is just the same as the panoramic video of football. Then we send it through our model architecture with corresponding team classifiers and top-view images. Pre-Trained Models In order to detect the player locations we are using a pre-trained model. Several models are present with varying ranges of accuracy and speed. We have tested the following models [5][2][13]. We have chosen the Faster RCNN model due to its balance of accuracy and speed. Tracking Players We sent our panoramic video from our football dataset and sent it through our model architecture in order to track the players. We finally get the player positions of our tracker on the reference field after applying the homographic transformation. This value is compared to the actual positions of the players provided by the football dataset.
V. RESULTS
In this section, we present the results obtained by applying our method on National Hockey League (NHL) dataset.
We show a comparative study between various methods of tracking the player. The methods used are Background Subtractor to identify Contours, Mean-Shift Tracking and Proposed Model Architecture.
After sending our video into our model architecture Figure 4a shows the detection of the bounding boxes of the players. After this we classify the teams based on their histograms to sort them into the two different teams. Boundary boxes whose ratios are inappropriate are eliminated and the Figure 4b shows the classification of the players. Black Boxes indicate a player of the black team.

White Boxes indicate a player of the white team. Now we qualitatively compare the detection of players using background subtraction and contour drawing by erosion and dilation and through our model architecture. Figure 5a shows the detection using the background subtractor method. Players that are slightly occluded or interacting become shown as one single player which is incorrect and inaccurate. However our model correctly identifies players that are close to each other even though they are extremely small as shown in Figure 5b.

Figure 6 shows the results of the shot segmenter in the proposed model. Figure 6a depicts a positive match of the court and Figure 6b shows a negative match where a close up of a player is found. The accuracy of our shot segmenter is 96.4%. As it is an implementation of the AlexNet architecture [7] it is quite fast and can be used to show the live segmentation of shots in broadcast sports.

Figure 7 shows the several cropped frames of tracking of a single player. Each frame is numbered and the pink box represents the actual position of the player. The blue box is the prediction made by our Kalman filter. The blue box is corrected using the correct location of the bounding box(obtained from our ML model). After frame number 16 the Kalman filter is no longer corrected and the blue box shown is only from the Kalman predictions. Now the Kalman filter can now be corrected using the ML prediction model every few frames and hence the predictions also become accurate. We have found that if we do not correct the filter and the player makes an abrupt movement then the filter will give inaccurate results. After testing for several frame lengths we found that if we correct the filter every 5 frames and predict the location in between we get good accurate tracking results. Hence we can improve the speed of simply using a Machine Learning by 5-fold as that detection frames will only be required to be found every 5 frames.
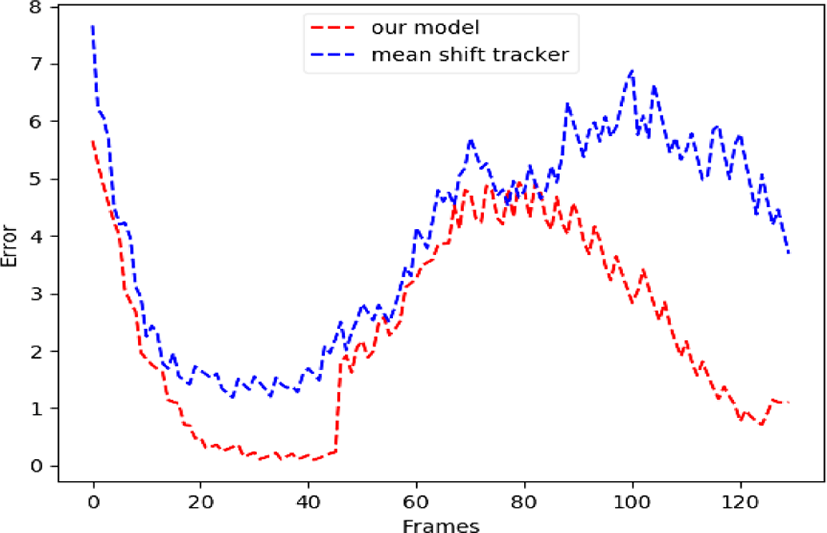
Figure 8 shows a comparative study of tracking error based on the ground truth provided by the football dataset. We compared the proposed model Architecture to the Mean shift tracking Algorithm to show the error with respect to time.
The error is calculated as
As we can observe our model does significantly better than a standard mean shift tracker. At most points our model finds the player more accurately. Initially the mean shift tracker also tracks the player accurately in the beginning. However as we can see towards the end it starts to create large error losses. This is because in fact the meanshift tracker loses track of the player and starts to track the grass behind him and remains stationary for a certain time. During this time the player moves away the distance between them increases.
VI. CONCLUSION
In this paper, we have developed a simple and effective model with low overhead which provides accurate results to track players in broadcast sports. We demonstrated the potential of machine learning and computer vision to track players in robust situations, such as those of evening matches, occluded situations, and even fast moving players with highly dynamic positions. Some real world applications of this paper could be to provide statistical information that could be valuable to sports training that effectively identify player’s strengths and weaknesses. Another application could be track players in live broadcast sports videos and give accurate and live information regarding the players just by using the video feed. This is only a tip of the iceberg and there is a lot of scope for applying machine vision algorithms for sports analytics and it is an emerging field.