I. INTRODUCTION
A large number of centrality metrics for various usages have been created over the years by network researchers. These centralities contributed significantly to analyzing and studying the structural properties of networks and individual characteristics of the nodes in complex networks. Centralities are used in identifying leaderships and influencer nodes in social networks [1], discovering important functionalities and structures in the decomposition of virus and brain networks [2-3], studying the spread of infectious diseases or information [4-6], segregating networks into small components [7], and analyzing the performance of Ad hoc networks [8-9].
Recent studies on degree centrality [10-13] introduce new collective centralities that are defined from the degree centrality of nodes in the neighborhood. Local centrality [10] uses the number of the nearest neighbors and the next nearest neighbors of a node as the neighborhood information. The local centrality of a node is the sum of the neighborhood information of the neighbors of that node. Collective Influencer [11-12] introduces a new perspective of centrality that the centrality of a node is defined from the collective centrality of all nodes on the ball having a certain distance from the node. A study in [13] proposes a centrality for identifying influential nodes which uses the coefficients based addition of the degree centrality of a node and the cumulative degree centrality values of the nearest neighbors of that node. A centrality score called Ing is proposed in [14] which assigns an initial value (i.e. degree centrality) to each node and repeatedly transforms the values of each node based on a transformation matrix. This process is repeated n times (algorithm parameter) to find the final Ing score.
Betweenness centrality (BC), which computes a rank for each node based on the role in communication between other nodes, is a popular measure to analyze networks [15-18]. Betweenness centrality highlights bridging nodes that have a high impact on information exchange. The centralities based on bridging nodes are often neglected in previous studies [18]. In this study, we propose a collective betweenness centrality (collective BC), which computes the node centrality in the context of the collective bridging centrality. The collective betweenness value of each node is defined by the cumulative betweenness values of the nodes that are located within the ball, where the ball is the set of nodes within D distance (a given parameter) from a node in the network.
The experimental results show that the nodes identified by the collective BC can be influential spreaders under the SIR model. It is able to identify the nodes that become important nodes when the normal flow of information disrupts. We will study collective BC measurement and its correlation with another state-of-the-art centrality measurement in Section II. Section III covers an application of the collective BC with the susceptible-infected-recovered (SIR) model [4, 19] on five real-world networks. The final section gives a conclusion.
II. COLLECTIVE BETWEENNESS MEASUREMENT
The shortest path betweenness measures the amount of information that passes through the nodes of a given graph considering that the information travels in the shortest paths. Therefore, the betweenness value of a node is calculated as the fraction of the number of shortest paths passing through that node by the number of all the shortest paths. The betweenness value of v is given by g(v) function as shown in Equation 1 where σst(v) denotes the number of shortest paths passing through node v and σst denotes the number of shortest between s and t nodes. For simplicity, we may simply call shortest-path betweenness as betweenness (BC).
In the shortest path betweenness, the nodes and edges involved in the current short path communication are highlighted and got high scores. There are some nodes and edges that are vital for communication if some disruption happens in the current short path communication.
Definition: some nodes and edges that are vital for communication if some disruption happens in the current short path communication are called “backbone nodes” for communication.
The proposed collective betweenness centrality ranks the backbone nodes in higher positions. The collective betweenness of a node is defined as the sum of betweenness values of the nodes located within D distance away (measured in hops) from that node.
In Equation 2, d(u,v) denotes the distance between u and v nodes measured in hops. In other words, collective BC sums all the betweenness values within the ball centered at the node v in addition to the betweenness of the center (node v). It gives more importance to the surroundings of the node since the betweenness sum of surrounding nodes usually exceeds the betweenness value of the node.
We used Spearman’s ρ correlation to analyze the relation of collective betweenness value with respect to three other centrality measurements -- degree centrality, closeness centrality, and betweenness centrality. For this measurement, the collective betweenness algorithm is run with D=1 and D=2 parameters on the datasets, and the correlation score are given for each centrality compared against collective betweenness for each dataset in a row in Table 1. Also, the mean correlation is calculated for each centrality to see the overall relationship of collective betweenness with others. The analysis shows that degree centrality and betweenness centrality are quite different from collective betweenness centrality for both D=1 and D=2 parameters. When D=1, the mean of coefficient ρ is 0.62 and 0.57 for degree and betweenness centralities respectively. When D=2, the mean of coefficient ρ is 0.63 and 0.58 for degree and betweenness centralities respectively. It seems that the distance parameter doesn’t affect the correlation between the centralities as the correlation increases on some networks and reduces on the other networks when the distance increases. Strangely enough, closeness centrality shows a high correlation to the collective betweenness scoring 0.87 and 0.89 for parameters D=1 and D=2 respectively. When D=1, the lowest coefficient for closeness centrality is 0.77 for netscience and the highest is 0.97 for email network. When D=2, the lowest is 0.70 for facebook and the highest is 0.98 for email network. This means that collective BC is quite correlated with closeness centrality for the most cases, although there may be some networks that make collective BC quite different from closeness centrality at least for these two depths.
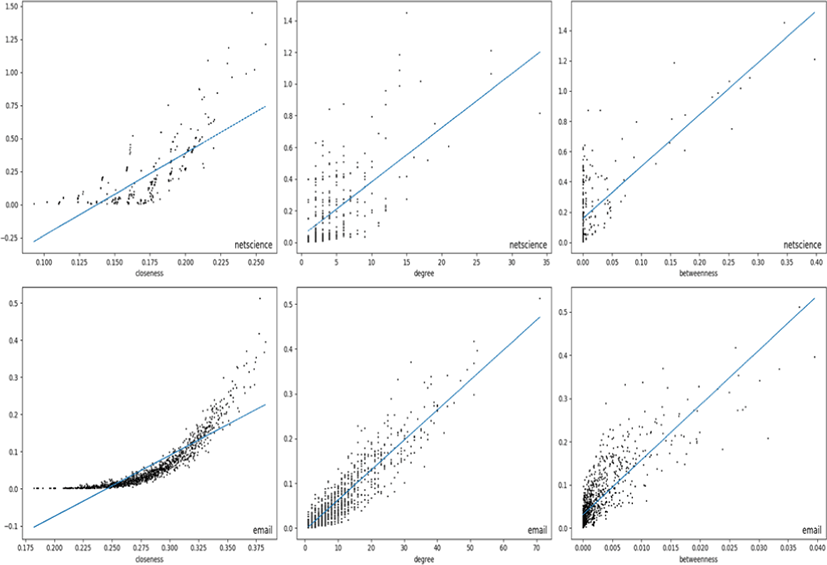
Scatter plots of collective BC of the nodes in email and netscience networks are shown in Fig. 1. The collective BC (D=1) of the nodes are compared against their closeness, degree, and betweenness centralities. A median line is drawn for better clarification. The correlation coefficient in netscience network is 0.77, 0.46, and 0.47 for closeness, degree, and betweenness centralities respectively and it can be observed in Fig. 1. Most of the nodes in the third column (betweenness) are packed together around 0 betweenness showing that it’s not correlated with collective betweenness. The correlation with closeness can be seen in the first plot of netscience as we can see that when the closeness centrality increases, their collective BC also increases. High correlation with closeness, degree and betweenness centralities observed in email network of the figure matches with the data in Table 1 as their correlation coefficients are 0.97, 0.89 and 0.84. The highest correlated centrality is closeness and its plot in the first column of email network in the figure shows a nice concave shape as the closeness centrality value increases. The degree centrality of email network shows a linear dependency on the collective betweenness except little bit clustering along the vertical axis that means degree centrality doesn’t have clear ties with collective BC for those nodes. Obviously, the nodes with the same degree don’t necessarily have the same collective BC values. But, it’s still worthwhile to see that the correlation coefficient in this comparison is pretty much dependent on the structure of the network.
III. EXAMPLES AND APPLICATIONS
facebook is a Facebook community network where edges represent friendship and vertices represent one’s profile. It was first used in [20]; grqc graph is a citation network of physicists working in General Relativity and Quantum Cosmology. They can be downloaded from snap.stanford.edu; blog network contain communication networks of the blog owners on the Windows Live Spaces; email is a network made out of email communications of University Rovira i Virgili [21]; netscience is a co-authorship of scientists on network science. We used only the greatest connected component of this graph.
| Networks | |V| | |E| | Degree_avg | Max_degree |
|---|---|---|---|---|
| Grqc | 5,241 | 14,484 | 5.53 | 81 |
| 4,039 | 88,234 | 43.69 | 1,045 | |
| Blog | 3,982 | 6,803 | 3.42 | 189 |
| Netscience | 379 | 914 | 4.82 | 34 |
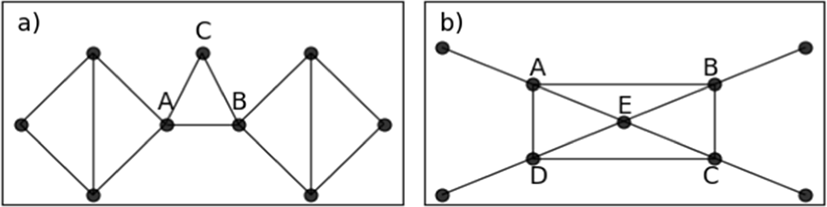
In this subsection, we examine the difference between the shortest-path betweenness and collective betweenness centralities on example networks. We focus on the nodes getting a lower rank (score) in BC, but a higher rank in collective BC with D=1. Let’s see two simple examples which are presented in Fig. 2. BC and collective BC scores are computed and reported in Table 3
| Node | BC | Collective BC | |
|---|---|---|---|
| Fig. 2(a) | A | 0.54 | 1.29 |
| B | 0.54 | 1.29 | |
| C | 0 | 1.07 | |
| Fig. 2(b) | A | 0.30 | 0.99 |
| B | 0.30 | 0.99 | |
| C | 0.30 | 0.99 | |
| D | 0.30 | 0.99 | |
| E | 0.10 | 1.29 |
Node C in Fig. 2(a) has a zero BC score. In the real-world scenario, node C has somewhat participated in communication between nodes in Fig. 2(a). At least, if the link between node A and B is removed or de-activated, node C becomes vital for communication in this network. Although node E in Fig. 2(b) has four neighbors with high BC scores and is located in a more central position, it gets a lower BC score than its neighbors. Node E in Fig. 2(b) ranks first by the collective BC score. This node has a backbone role in communication. In addition, if some links in the short paths are removed or de-activated, e.g. link (A, B), node E gets a higher BC score. Our proposed collective BC highlights these backbone nodes.
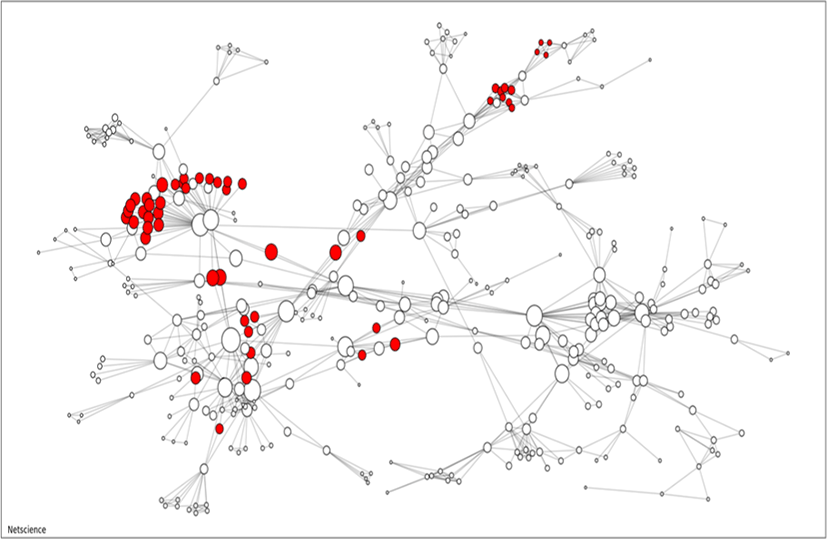
A co-authorship network with 379 nodes is illustrated. We focus on the high-rank difference in two ranking methods, i.e., nodes getting lower rank (score) in BC but higher rank in collective BC with D = 1. The co-authorship network is presented in Fig. 3, where the nodes getting more than 120 ranks higher in collective BC are colored in red. The sizes of nodes represent the collective BC scores.
The backbone nodes identified by our collective BC may serve as influential spreaders in networks. Susceptible-Infected-Recovered (SIR) model is one of the basic models that evaluate the spreading process in networks [4,19]. There are three compartments in this model: (i) Susceptible S(t) represents the number of the people who are not infected by an infectious disease at the time t; (ii) Infected I(t)represents the number of infected people (not yet recovered) at the time t; (iii) Recovered R(t) represents the number of recovered people (they don’t spread disease any more) from the disease at the timet. At first, there is only one infected node. In each time step, each infected node is able to infect one of its susceptible neighbors with the probability λ. We used λ = 1 for simplicity in evaluating the model just as described in [10]. An infected node is able to recover with the probability where dgree_avg is the average degree of the graph shown in Table 1, at each step. When the number of infected nodes becomes zero, the process terminates. In order to investigate the influence of a single node that started the infection, the function F(t) = I(t) + R(t) is used. F(t) becomes constant after some time tc and this value at tc becomes the influence of the starting node. The higher the value of F(tc) the more influence (more devastation) the node has on the spread of disease or information in networks [10].
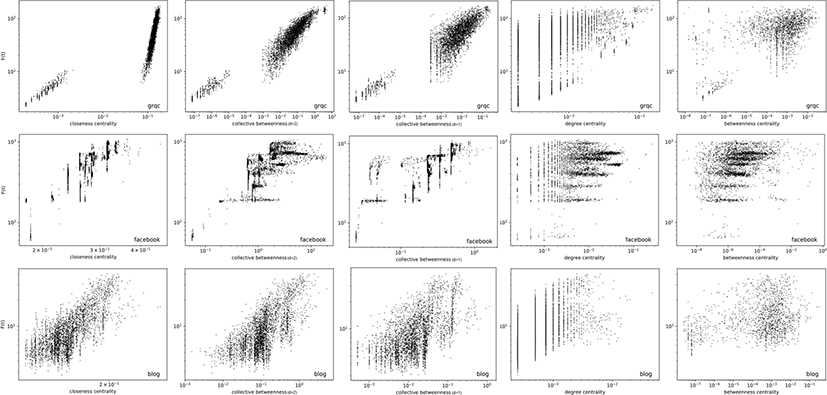
We examine the relation between the rank obtained by the collective BC and the influence score (F(t = 10)) computed by the SIR model. The relation of the two measurements is compared with other centrality measures (closeness, degree, betweenness) on three networks (grqc, facebook, blogs). The results are presented in Fig. 4. The plot of degree centrality (fourth column) has long vertical lines that indicate nodes with the same degree can be a totally different influence in spreading, F(t). The plot of betweenness centrality (fifth column) covers the almost whole area of the square. This indicates no clear relation between BC and influence in spreading, F(t). Our collective BC (second and third column) is relatively better correlated with the node’s influence in spreading than that of degree and BC. In another words, the node with a high collective BC rank also has a tendency to have a high influence in spreading. The rank of collective BC (D = 2) is comparable with the rank of closeness centrality.
IV. CONCLUSION
We have proposed a new centrality that is defined from the collectivity of betweenness centralities in the neighborhood. The proposed centrality highlights the nodes that are involved in the backbone role in the communication of networks. An application in identifying influential spreaders is examined under the Susceptible-Infected-Recovered (SIR) model. Experimental results show that the new centrality successfully identifies the influential spreaders in networks.
CODE AVAILABILITY
The codes and other materials used in this study are available at https://github.com/denduuyum/collective_betweenness.



