I. INTRODUCTION
Dance Quality Assessment (DanceQA) evaluates techniques of performers dancing to music and provides their dance performance quality numerically. Along with people’s interest in dancing, the size of the industry market related to dancing has been growing over recent years [1], and a large number of dance videos have been uploaded on social media. In addition, Breaking, a style of dance that originated in the United States in the 1970s, has been chosen to feature on the Paris 2024 Olympic sports program as a new sport [2]. In response to this general interest, the criteria for dance performance evaluation have evolved specifically. Researchers have studied guides for dance performance evaluation by judges considering physical ability and rhythmic accuracy of the performers [3-5]. However, the hurdle of specialized knowledge makes non-experts inaccessible to DanceQA, and this leads to the need for DanceQA algorithm which can learn the knowledge and evaluate automatically.
The automation of DanceQA saves evaluators’ efforts by providing score predictions of dance performance quality. When evaluating dance performance, the human evaluators must watch every single video and determine performance rating while closely looking into dance motions. Without the help of automated DanceQA, the dance performance evaluation requires a significant amount of time for the evaluators to watch a lot of dance videos which are few minutes long. The automated DanceQA provides dance performance scores and helps to select candidates which the evaluators should watch for sophisticated evaluation. This secondary role not only saves human resources, but also allows for more efficient assessments by focusing the expert’s efforts on critical parts.
The automated DanceQA is able to fulfill a key role as a main evaluator in situations where an expert is not available. Since existing dance performance evaluation methods [3-4] are very dependent on the dance experts, they are rarely used in everyday situations due to their low accessibility. It is difficult for non-experts to utilize DanceQA, which requires a lot of time and effort to learn related expertise for accurate evaluation. The automated DanceQA method can replace this process by training correlation between dance performance and its quality score with high availability.
The automated DanceQA provides analysis of dance performance at joint or frame level to give feedback to a performer. In dance performance evaluation, the human evaluators usually give comments on the performance to the performer. Since the human evaluators are not always available, previous works [6-8] have analyzed dance performance only the kinematic data of dance motion like joint positions or joint angles. This information is only shown as a graph and is not visualized for human perspective, making it difficult to understand intuitively. Deep learning techniques which try to capture neural activation [9] or an attention weight [10] have been developed to analyze prediction results visually. DanceQA networks can visualize the activation of spatial joints or temporal frames which contribute to the dance quality score by utilizing these techniques.
In this paper, we propose Dance Quality Assessment Framework to handle issues and include datasets, dance quality measures, and regression networks for DanceQA as shown in Fig. 1. 3D motion data are collected in two ways, 3D pose estimation and motion capture, to build DanceQA dataset for subjective test which provides a dance quality score by ranking performers from relative comparison results. For dance quality labeling, Performance Competence Evaluation Measure (PCEM) [11] guides are adopted, and the subjective test involves comparing a pair of dance performance and choosing the relatively better one following the guides. To capture important elements of dance motion, Kinematic Information Measure and Kinematic-Music Beat Alignment are designed by examining kinematic statistics and multimodal similarity. To target the dance quality score ranked by the subjective test, the regression networks sufficiently long and dense 3D motion by considering diverse characteristics of 3D skeletal sequence and fusing them in transformers while referring results of the dance performance measures. Lastly, to measure kinematic and music beat alignment, multi-modal attention blocks are designed to train correlation between multi-modal inputs, dance motion and music.
At first, 3D motion data are inferred by 3D pose estimator from RGB videos, which are captured by the public and uploaded to the web. These videos have diversity in terms of dance quality, but the inferred 3D motion is not accurate due to limitations of the estimator. By leveraging kinematic characteristics of the 3D dance motion, dance proficiency is measured by the kinematic information entropy and the multi-modal similarity based on previous quality assessment methods [12]. A new representation of 3D motion is proposed to link spatially or temporally adjacent joints according to natural connection of skeletal structure. Existing spatial or temporal difference vectors [10] are replaced by the proposed dependency inputs, which show the higher correlation between subjective scores and score predictions in experimental results. To regress the dance quality scores from 3D motion data, we employ transformers [13] as a baseline, which trains spatial or temporal dependency via self-attention matrices. After processing each input, two streams are fused in fusion transformers instead of ensemble learning which is used commonly in human action understanding. Multi-modal transformers learn correlation between the trained dance motion features and music features for beat alignment and the output features are regressed by the subjective quality scores.
In summary, this research presents a novel approach to dance performance evaluation by integrating kinematic information entropy and multi-modal beat similarity. In section II, we propose the new dance quality transformers model, and we will show the performance through many experiments in Section III. The originality lies in leveraging deep learning to automate and enhance the objectivity of dance quality assessment. The main contributions of the proposed DanceQA framework can be included as follows:
-
Dance performance measures are proposed to leverage kinematic characteristics and beat alignment for examining important factors in DanceQA.
-
A new representation of 3D skeletal motion is proposed to link spatially or temporally adjacent joints for natural connection of skeletal joints.
-
Intra-motion transformers are designed by embedding the kinematic entropy to capture the dance quality in spatial dimension and fuse the features with different characteristics. The dance motion features, and music feature are trained together for multi-modal learning by the proposed inter-motion and multi-modal transformers.
II. DANCE QUALITY TRANSFORMERS
Overall network architecture is shown in Fig. 2. The dataset including 3D dance motion data and its label for DanceQA is stored in the database of Fig. 2 and 3D skeletal data are represented by the features with different characteristics and used as inputs to these networks. Intra-motion Transformers learn spatial dependency of each feature within the spatial tokens based on entropy-embedded attention, and these features are fused by Fusion Spatial Transformers to consider diverse characteristics of features. Temporal dependency is trained with following Inter-motion Transformers, and music features are trained together in multi-modal Transformers to align kinematic and musical beats. The details of the proposed networks for 3D DanceQA will be described in following subsections.
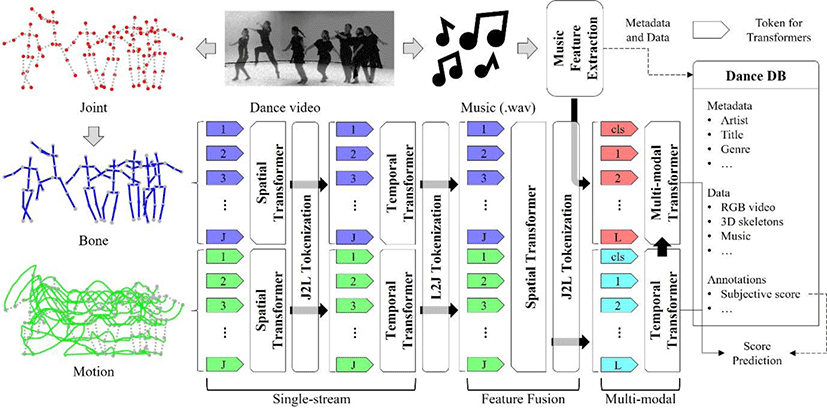
The Dance Quality Assessment predicts dance quality score from dance performance in terms of 3D human motion. The 3D human motion data consists of 3D skeletal sequence that articulates human motion with major joint positions. Let p be joint positions of the skeletal sequence and p is defined as follows:
where T and J is the number of frames and joints of the 3D skeleton sequence. The dance quality score y is labeled and coupled with its corresponding 3D skeleton sequence p. The DanceQA dataset can be defined as follows:
where N is the number of data pairs in the dataset.
Previous works usually used these joint positions or their spatial and temporal difference vectors, which represent bone and velocity vectors, to learn semantics of 3D skeleton sequence. In DanceQA, the body shape and movement in dance performance can be articulated by these two features, which are very useful to predict its dance quality score. These features are also used in the proposed network to consider diverse characteristics of dance motion. However, these features could not represent real bone and velocity vectors because their start and end positions of the vectors disappeared as shown in Fig. 3(a). They are just vectors starting from the origin, and learning algorithms cannot understand the bone and velocity information the way human perceives.
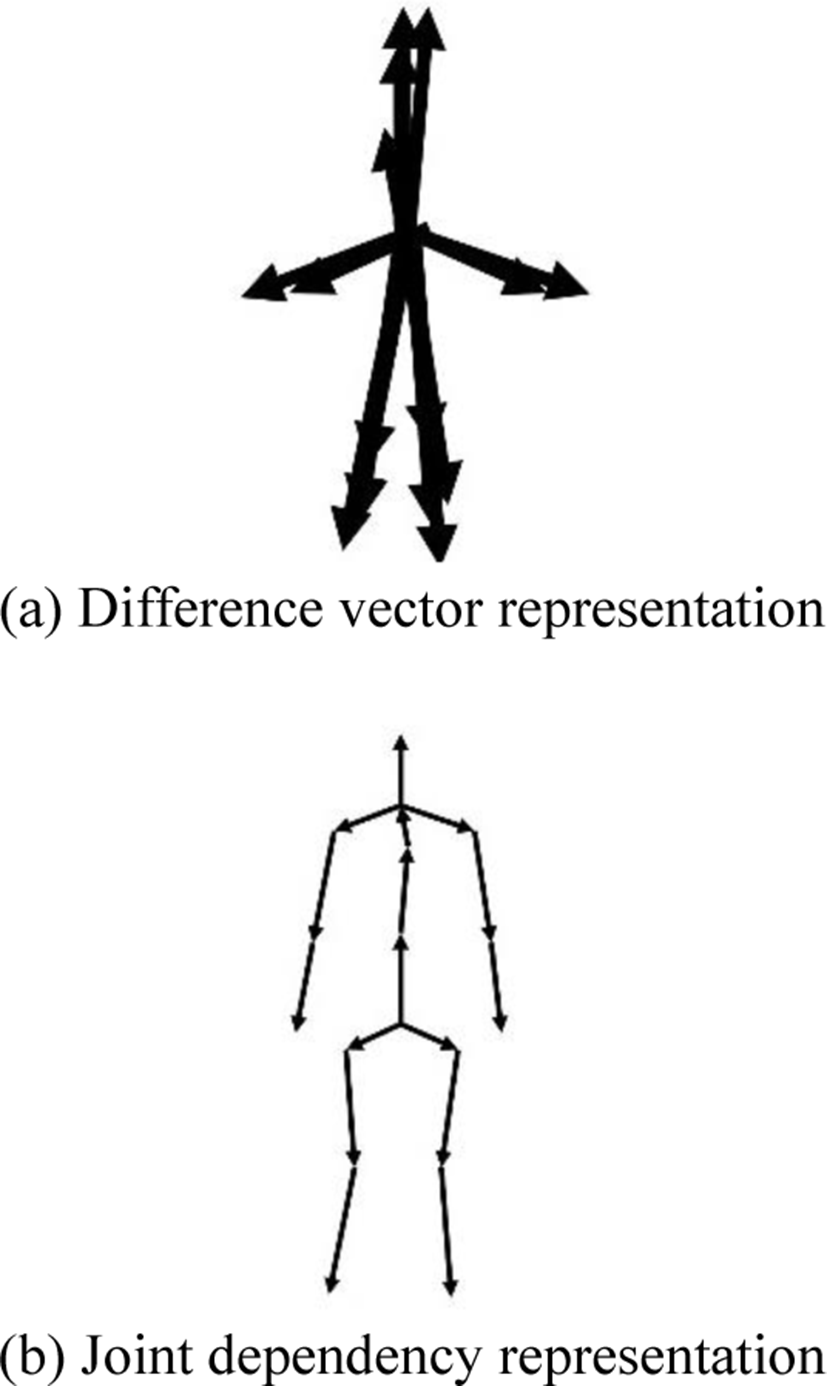
To help networks remember the information, as shown in Fig. 3(b), we propose joint-dependent features which contain the start and end positions of the bone and velocity information instead of spatial and temporal difference. This is more similar to human perception than the difference vector representation when observing the skeleton sequence. The bone dependent (spatially joint-dependent) features b are represented as follows:
where ⊕, i1, i2 is the operation to concatenate vectors, the start and end joints of ith bone, respectively. The motion dependent (temporally joint-dependent) features m are represented as follows:
The spatial and temporal dependency of skeletons is embedded in these features respectively while preserving joint positions. In transformers, it is difficult to reflect the joint relationship without any constraint on spatial or temporal self-attention matrices. Nevertheless, the dependent features make it possible to train the bone and motion vectors simply by connecting dependent joints in preprocessing step without information loss and improve dance quality prediction performance in DanceQA.
Previous Skeleton has the characteristics of both natural language and images in spatial and temporal dimensions, respectively. The joints have specific semantics such as neck, hip, shoulder, elbow, wrist, knee, ankle and so on like words in natural language, but the frames are not semanticcally separated like pixels in images. Thus, each joint is used as a spatial token and multiple frames are used as a temporal token to explore spatial or temporal dependency in transformers.
The spatial and temporal tokens are described as the red box and the blue box, respectively, in Fig. 4. The input features are reshaped into the spatial token, which is the shortest unit to analyze long dance sequence. The ith spatial token of the jth joint XS,(l,j) is defined as follows:
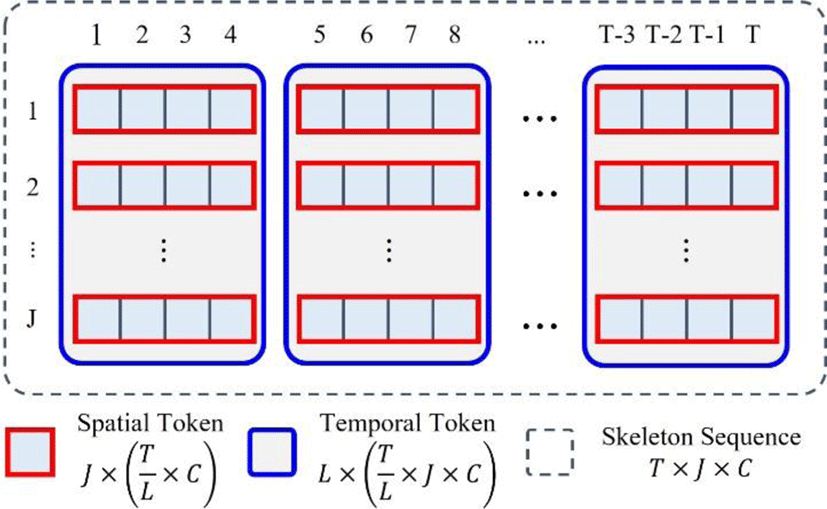
where L is the number of tokens. The spatial tokens are concatenated as the temporal token including all the joints. The lth temporal token is defined as follows:
Each spatial token is embedded with the channel size CT/L for the spatial transformers, and the temporal tokens are used as inputs for the temporal transformers after J2L Tokenization where L is the number of the temporal tokens. The number of frames within the token T/L is very important factor for DanceQA. The temporal token with the small number of frames cannot represent sufficiently the unit motion while it is difficult to understand the dance sequence if the unit motion is too long. We find the optimal T/l empirically by testing multiple values in next Section.
The Intra-motion transformers are designed to train not only spatial dependency of diverse skeletal features but also short-term characteristics of the unit motions. After the input embedding, the positional embedding is injected for the transformers to make use of the joint positions. For the inter-motion transformers, outputs of the intra-motion transformers are concatenated into the temporal token. As shown in Fig. 4, all the spatial tokens within the unit motion are gathered together for the temporal token.
After the intra-motion and inter-motion transformers, the correlation between kinematic and musical beats are trained by the multi-modal transformers in Fig. 2. The skeletal features are trained by self-attention of the inter-motion transformers while the music feature is trained by cross-attention of the multi-modal transformers.
The proposed overall network architecture is proposed as shown in Fig. 2 consisting of the input features and transformers. Single-Stream Transformers (SST) learn spatial and temporal dependency of each feature. Feature Fusion Transformers (FFT) learn dependency between multiple features, which are trained sufficiently from each SST. Understanding each feature independently helps to fuse multiple features together. At last, for multi-modal learning between kinematic and music features, multi-modal transformers and inter-motion transformers are trained together. The inter-motion transformers learn temporal dependency of the outputs of the FFT only by their self-attention. The multi-modal transformers learn correlation between the musical features extracted from wave files and the kinematic features from the inter-motion transformers. The quality tokens denoted as Q of multi-modal beat alignment and inter-motion transformers in Fig. 2 are regressed by the linear layer to predict the dance quality score. Mean Squared Error (MSE) is employed as loss function to train the proposed transformers by decreasing the difference between dance quality prediction and its subjective score.
III. EXPERIMENTS
To measure performance of the proposed dance quality measure and DanceQA networks, we suggest two protocols. Protocol I contains only ‘Dynamite’ of BTS. 23 videos are used for training and 10 videos are used for testing. Protocol II contains only ‘Kill this love’ of BLACKPINK. 21 videos are used for training and 10 videos are used for testing. Protocol I and II are tests to measure the quality of dance performance for the same choreography.
To show the performance of the proposed transformers, ST-Graph Convolutional Network (GCN) [14], AGCN [10] and FACT [15] are tested with various features. ST-GCN and AGCN are the most popular graph convolutional networks in action recognition. These networks build adjacency matrices according to the natural connection of skeleton and convolve neighbored joints. FACT uses full attention to find kinematic and musical relationship at frame level without considering spatial structure within a frame.
For performance comparison, we used two metrics: Pearson Linear Correlation Coefficient (PLCC) and Spearman Rank Correlation Coefficient (SRCC). PLCC measures the linear relationship between two continuous variables. It provides a value between −1 and 1, where 1 indicates a perfect positive linear correlation, −1 indicates a perfect negative linear correlation, and 0 indicates no linear correlation. Moreover, SRCC measures the strength and direction of the monotonic relationship between two ranked variables. It is a non-parametric measure and provides a value between −1 and 1, similar to PLCC.
FACT and ST-GCN shows the lowest and the highest correlation, respectively, among the other methods. The tokens of FACT include both 3D skeletons and musical features, which blend and seem to disturb predicting their dance quality score, and this leads to the design of the multi-modal transformers that keep the kinematic feature from the musical feature. ST-GCN and AGCN have their adjacency matrices, which define connections among joints or bones. This definition may be very good constraint on action recognition but does not help to find salient joints in the DanceQA. There are salient joints, especially an ankle in this case, which have high correlation with the dance quality score. This distinct point leads to using transformer blocks to identify salient joints readily for dance quality prediction.
For ablation study, three types of networks are listed in Table 1 with various input features. Inter-motion only considers the temporal relationship between the tokens. Intra-motion+Inter-motion handles both spatial and temporal attentions sequentially and show performance improvement compared to Inter-motion only. Intra-motion+Inter-motion +Multi-modal BA covers cross-modal correlation between kinematic and musical features beyond spatial and temporal modeling and show the significance of musical information in the DanceQA. Intra-motion+Inter-motion+Multi-modal BA+KE embedding adds kinematic entropy embedding to attention matrices in intra-motion transformers.
There are the performance improvements with additional transformers or musical features. Inter-motion only shows the lowest accuracy in the ablation study, and the addition of intra-motion transformers makes focused on the salient joints. As previously mentioned about FACT, it is very critical for the quality regressors to figure out spatial characteristics for dance quality prediction. Also, cross-attention of multi-modal transformers improves the prediction performance by learning cross-correlation between kinematic and musical features regardless of the feature type.
IV. CONCLUSION
In this paper, we present a DanceQA framework based on transformer architecture. The proposed dance quality measures, kinematic entropy, and multi-modal beat similarity, remarkably distinguish salient joints in the DanceQA. The proposed DanceQA transformers capture salient body parts and frames in their attention weights that contribute to the dance quality prediction while outperforming other GCNs and transformers. We present various experimental results and analyses which show how to capture the dance quality. This framework demonstrates the feasibility of the DanceQA in 3D skeleton domain for future works. We train only single choreography, but the DanceQA framework needs to handle more than two choreographies for evaluating unseen choreography.

