I. INTRODUCTION
Accurate age estimation from facial images has attracted considerable attention in the fields of computer vision and biometrics. Age information derived from facial appearance is essential for various real-world applications, including age-based access control, personalized services, social media content filtering, and demographic analysis [1]. Compared to categorical tasks such as gender classification or facial expression recognition, age estimation is inherently more challenging due to significant variations in facial features caused by aging, genetics, lifestyle, and environmental factors [2].
In recent years, deep learning approaches, particularly convolutional neural networks (CNNs), have demonstrated remarkable success in visual recognition tasks, including age estimation. However, the performance of CNN-based age prediction models remains limited in practice, mainly due to data imbalance issues present in publicly available facial age datasets [3]. One notable example of a publicly available dataset for age estimation is the FG-NET aging database [4], which contains facial images of individuals ranging in age from 0 to 69 years. Despite its popularity in the field, the FG-NET dataset exhibits a significant age-dependent sampling bias, as illustrated in Fig. 1.
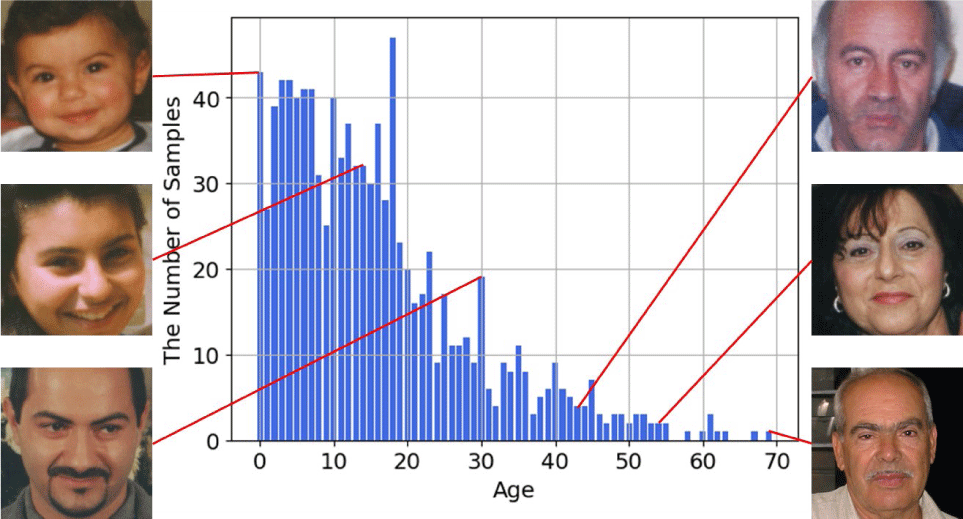
As shown in the figure, the number of facial images varies considerably across age groups. There is a high concentration of images for individuals in their infants, teens and twenties, while the number of samples for elderly individuals (over 60 years) is relatively sparse. This imbalance leads to biased learning and limits the generalization performance of CNN-based models. In particular, the model tends to perform well on age ranges with abundant training data, while prediction accuracy deteriorates for underrepresented age groups [5]. Although various data augmentation techniques have been proposed to mitigate such imbalance in classification tasks [6-8], limited research has explored effective augmentation strategies tailored for regression-based age estimation.
To address this limitation, we propose a targeted data augmentation approach designed to alleviate the effects of age-dependent sampling bias and data imbalance. The method generates synthetic facial images for age groups with limited training samples, thereby improving the performance and robustness of regression-based age estimation models.
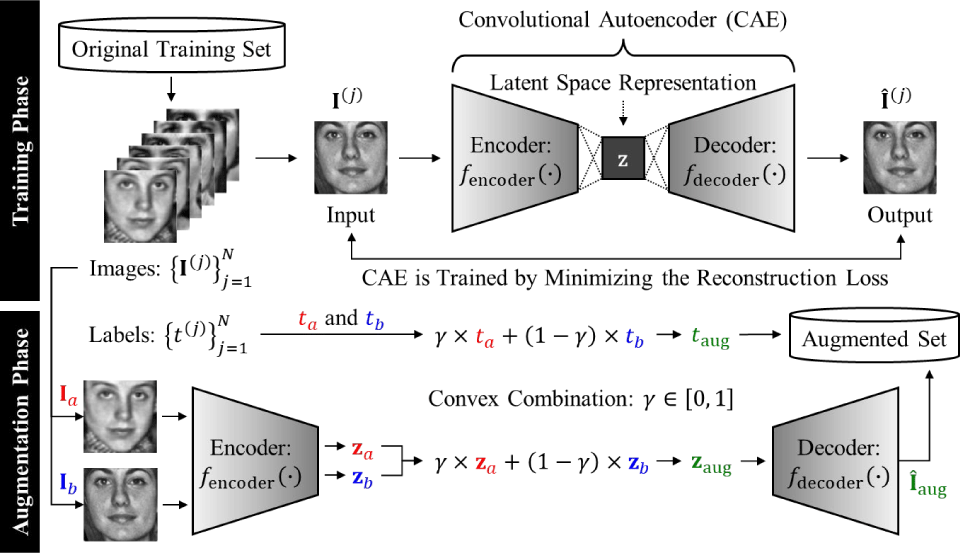
The proposed augmentation strategy is based on a convolutional autoencoder (CAE) specifically tailored for facial age estimation. The available facial images are grouped into age intervals of uniform size to divide the full age range of the dataset. A separate CAE is trained for each group to learn latent representations of facial features. During the augmentation phase, new synthetic facial images are generated by feeding the decoder with a convex combination of the latent vectors of two randomly selected images from the same age group. The corresponding age label of each generated image is calculated as a weighted average of the original age labels.
Unlike previous approaches that rely on generative adversarial networks (GANs) or variational autoencoders (VAEs), which often require complex training objectives and are prone to instability, the proposed CAE framework offers a simpler yet effective alternative for generating realistic and structurally consistent synthetic face images within each age group. By learning low-dimensional latent representations from grayscale facial images, our method enables interpolation in the latent space to synthesize new age-preserving samples, thereby mitigating the issue of data imbalance.
In contrast to GAN- and VAE-based augmentation methods, which typically involve explicit modeling of the aging process or identity-to-age transformations, our CAE-based approach synthesizes age-representative samples through latent space interpolation between real faces within the same age group. This design helps preserve realistic facial structure and texture while addressing data imbalance in a task-specific manner.
By applying the proposed data augmentation technique to underrepresented age groups, we effectively alleviate the data imbalance issue and enhance the training process of CNN-based age estimation models. Experimental results demonstrate that our approach significantly improves age prediction accuracy, particularly for age ranges with limited training samples. The main contributions of this study can be summarized as follows:
-
We propose a novel data augmentation strategy based on CAEs to address age-dependent data imbalance in facial age estimation tasks. The proposed method generates realistic synthetic facial images through latent space interpolation, enabling effective training of age estimation models in underrepresented age groups.
-
We systematically evaluate the proposed augmentation method across six representative CNN architectures, including both randomly initialized and pre-trained models, under the leave-one-person-out (LOPO) cross-validation protocol using the FG-NET dataset. The results consistently demonstrate improved performance, particularly for models trained from scratch.
The remainder of this paper is organized as follows. Section II reviews related work in facial age estimation, including traditional methods, deep learning-based approaches, and data augmentation strategies. Section III introduces the proposed CAE-based data augmentation framework in detail. Section IV describes the experimental setup, dataset characteristics, and evaluation metrics, followed by a comprehensive analysis of the results. Finally, Section V concludes the paper and outlines future research directions.
II. RELATED WORK
Age estimation from facial images has been an active research topic in computer vision, with significant progress made through the application of machine learning and deep learning techniques. Existing methods can be broadly categorized into three groups: (1) handcrafted feature-based approaches, (2) deep learning-based approaches, and (3) data augmentation for age estimation, which have been explored to improve performance under diverse real-world conditions and data limitations.
Early studies on facial age estimation primarily relied on handcrafted feature extraction techniques to describe facial appearance, texture, and geometry. Methods such as local binary patterns (LBP) [9], histogram of oriented gradients (HOG) [10], and local directional and moment patterns (LDMP) [11] were widely adopted to capture age-related facial cues. Although these methods are computationally efficient and interpretable, they often struggle to generalize under unconstrained imaging conditions, including variations in lighting, pose, and facial expressions [12].
In recent years, researchers have explored combining handcrafted features with modern machine learning models to enhance age estimation performance, especially in scenarios with limited computational resources. For instance, Nagaraju and Reddy [13] proposed a hybrid model that integrates handcrafted features derived from local diagonal extreme patterns (LDEP) with deep features extracted using the Inception-v3 architecture. Their method demonstrated competitive performance on multiple age estimation datasets, highlighting the complementary benefits of combining traditional and deep feature representations.
Additionally, Khalifa and Sengul [14] investigated the fusion of LBP and HOG features with classical machine learning classifiers, including support vector machines (SVM) and k-nearest neighbors (KNN), for age group prediction. Their approach achieved high classification accuracy, reporting up to 99.87% on age estimation datasets, emphasizing the continued relevance of handcrafted features in efficient and interpretable age estimation systems.
These recent studies demonstrate that despite the dominance of deep learning, handcrafted feature-based approaches remain important, particularly for applications with limited hardware capabilities or where model transparency is prioritized.
The advent of deep learning, particularly CNNs, has significantly advanced age estimation tasks. CNN-based models automatically learn hierarchical feature representations from raw facial images, enabling improved performance compared to traditional methods. Several works have explored CNN architectures for age estimation, treating the problem as either a classification, regression, or hybrid task.
Classification-based methods formulate age estimation as a discrete categorization problem by dividing age into pre-defined groups [15]. Levi and Hassner [16] demonstrated the effectiveness of deep CNNs for age and gender classification tasks using unconstrained facial images, highlighting the superiority of deep learning over traditional handcrafted methods. Sheoran et al. [17] proposed an age and gender prediction model based on deep CNNs combined with transfer learning. Their approach utilized pre-trained networks to improve performance on relatively small-scale datasets, demonstrating the benefit of leveraging large facial image repositories for knowledge transfer.
Benkaddour [18] presented a CNN-based feature extraction model for age estimation and gender classification tasks. Their work emphasized the role of deep feature representations in boosting classification performance, particularly under varying imaging conditions. Mustapha et al. [19] developed a CNN model tailored for classifying facial images into distinct age groups. Through systematic experimentation, they validated the model’s robustness in real-world scenarios where age group boundaries are not always visually clear. More recently, Zhang et al. [20] introduced GroupFace, a method that addresses the severe class imbalance issue in age group classification. By incorporating a multi-hop attention graph convolutional network and group-aware margin optimization, their approach achieved improved accuracy, particularly for underrepresented age groups.
Regression-based approaches aim to predict continuous age values directly from facial images. Niu et al. [21] introduced ordinal regression with CNNs to model the age estimation task, highlighting the potential of multi-output frameworks for improving accuracy. Distance-based regression CNN models [22], advanced loss functions [23], and deep regression forests [24] have further refined continuous age prediction. Notably, Wang et al. [25] proposed an attention-based dynamic patch fusion approach to enhance face-based age estimation, where key facial regions are adaptively emphasized, leading to substantial improvements in regression accuracy.
Hybrid methods combine elements of classification and regression to exploit the strengths of both methodologies. Gao et al. [26] proposed a deep label distribution learning framework that accounts for label ambiguity, effectively blending classification and regression components. Duan et al. [27] introduced a hybrid CNN-ELM model for simultaneous age and gender prediction. Such hybrid approaches often yield better performance, particularly when dealing with the inherent uncertainty of age estimation tasks.
Despite these advancements, the performance of CNN-based age estimation models remains constrained by the quality and quantity of available training data. Public datasets such as FG-NET, MORPH [28], and UTKFace [29] have been widely utilized for age estimation research. However, these datasets often suffer from severe age imbalance, with a disproportionately low number of images for certain age groups, particularly elderly individuals. This sampling bias leads to degraded model generalization and reduced accuracy for underrepresented age groups.
Data augmentation techniques have been extensively applied to address data scarcity and imbalance issues in computer vision tasks [30]. Traditional augmentation methods include geometric transformations, color perturbations, and image flipping. More recently, generative models such as GANs and autoencoders have been leveraged to synthesize realistic images for tasks like face generation [31], domain adaptation [32], and attribute manipulation [33]. In the context of age estimation, several studies have explored synthetic data generation to alleviate data imbalance.
For instance, Makhmudkhujaev et al. [34] introduced Re-Aging GAN (RAGAN), which achieves personalized face age transformation by compelling the input identity to guide the generation process, resulting in high-quality age-progressed images. Another method utilizes VAEs for data augmentation. Chadebec and Allassonnière [35] proposed an efficient sampling technique from a VAE in low sample size settings, demonstrating significant improvements in classification tasks by generating synthetic data that enhances model training. Additionally, Alrubaye et al. [36] implemented advanced data augmentation and balancing strategies to improve human age detection using CNNs. By integrating datasets and applying novel augmentation techniques, they achieved a high F1 score, underscoring the importance of data diversity in model performance.
While these methods show promising results, they often require complex training procedures and may suffer from image quality limitations [37]. In this work, we propose a novel data augmentation method utilizing a CAE to generate synthetic facial images through latent space interpolation. Unlike existing GAN-based methods, our approach provides a simpler and more controllable framework for generating realistic images with continuous age labels, effectively addressing the age imbalance problem in facial age estimation.
III. PROPOSED METHOD
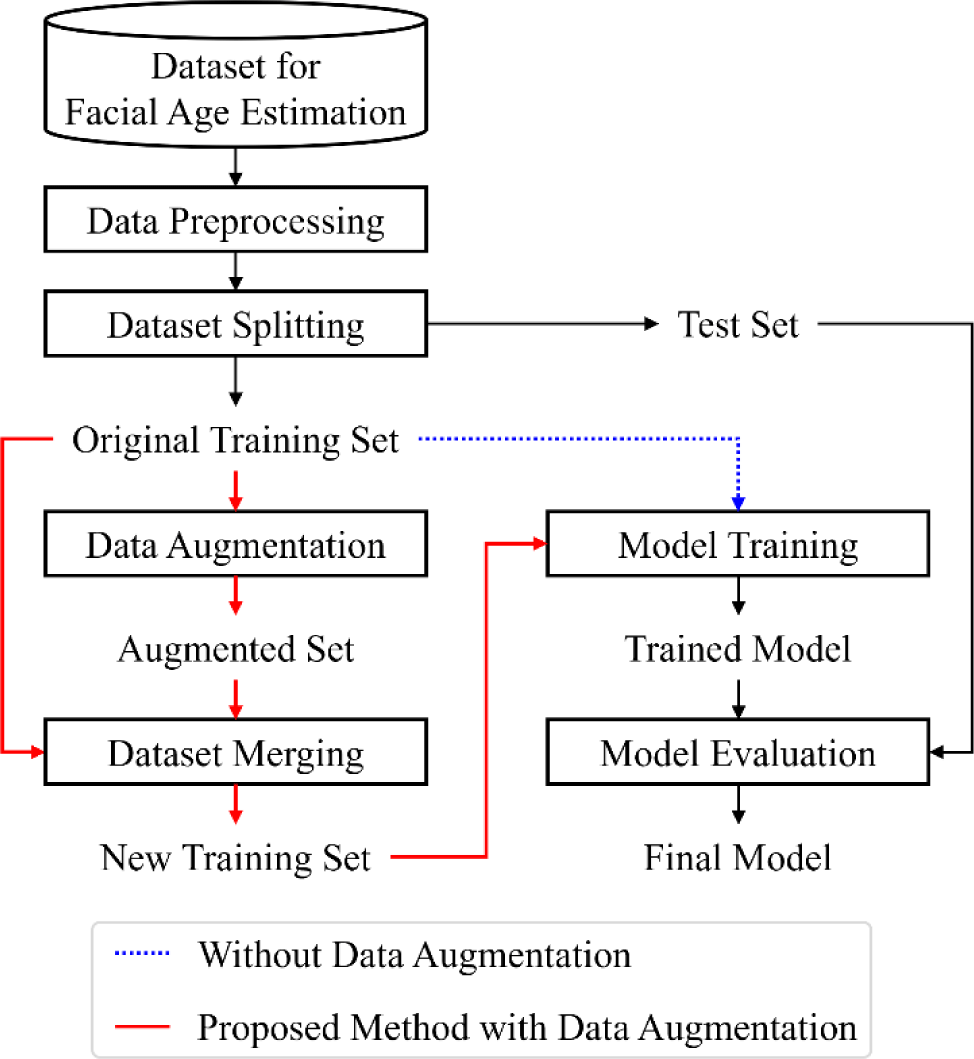
This section introduces the proposed data augmentation framework aimed at mitigating age-dependent sampling bias in facial image-based age estimation. The framework comprises two major components: (1) a robust data preprocessing pipeline for facial image normalization, and (2) the generation of synthetic facial images via a CAE. An overview of the proposed methodology is depicted in Fig. 2.
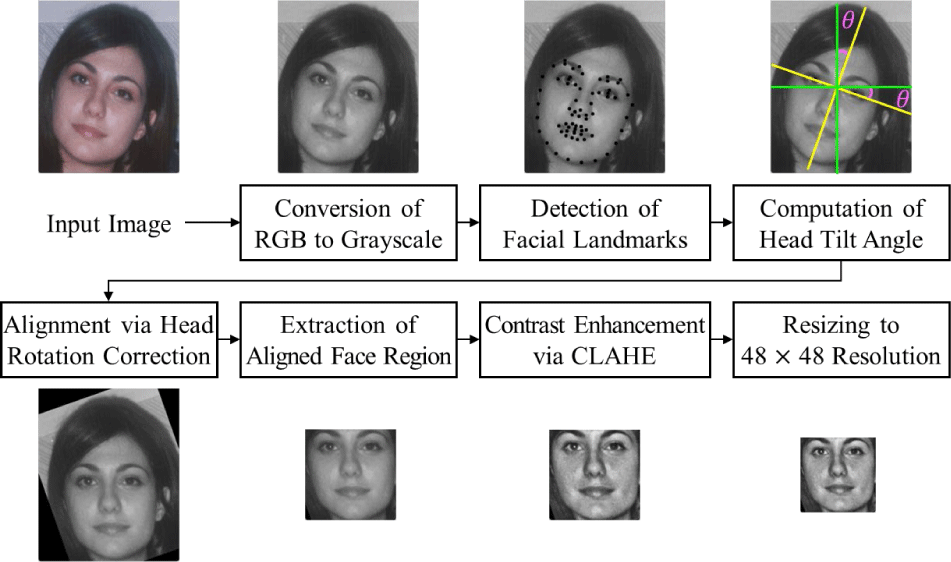
In order to minimize the influence of irrelevant factors such as skin tone variations and illumination differences on age estimation, a comprehensive set of preprocessing steps is applied to the input facial images. First, all facial images are converted to grayscale, as using color images may cause the model to rely on skin tone information rather than focusing on structural features that are more directly correlated with age.
Next, to ensure consistent facial alignment across the dataset, face alignment is performed based on facial landmark detection and geometric transformation. The specific type and number of detected landmarks depend on the employed detection algorithm. In this study, we utilize a pre-trained facial landmark detection model that identifies 68 two-dimensional (2-D) facial landmarks per image [4].
Let i be the index of a landmark, where i ∈ {0,1,⋯,66,67}, and let the position of the ith landmark be denoted as pi = (ui, vi). Among the detected landmarks, the left and right pupils correspond to indices 31 and 36, respectively. Their positions are represented as p31 = (u31, v31) and p36 = (u36, v36). To correct for head rotation and ensure horizontal alignment of the eyes, the angle θ between the straight line connecting the pupils and the horizontal axis is calculated as:
Regarding θ, it represents the degree of head tilt in the facial image. Using (1), an affine matrix A(θ) is constructed with the center of the image (cx, cy) as the rotation pivot:
where α=cos(θ) and β=cos(θ).
To align the facial image based on the positions of the pupils, an affine transformation is applied using (2). Let (x, y) represent the coordinates of a pixel in the original image prior to alignment, and let (x′, y′) denote the corresponding coordinates after the alignment process. The relationship between these coordinates is given by the affine transformation shown in the following equation:
This transformation, as described in (3), is applied to each pixel in the image to convert its original coordinate (x, y) to the aligned coordinate (x′, y′), thereby ensuring consistent orientation across all facial images. After alignment, the facial landmarks are updated by applying the same transformation, ensuring their positions remain consistent with the rotated image:
To localize the facial region within the image, an axis-aligned minimum bounding box is computed by identifying the minimum and maximum and coordinates among all detected facial landmarks. This bounding box serves as the basis for cropping the image, enabling the extraction of a tightly aligned facial region for further processing. Through this alignment and cropping process, variations in head tilt, rotation, and image framing are normalized, resulting in standardized facial images suitable for subsequent age estimation tasks.
To mitigate the effects of varying lighting conditions across images, contrast limited adaptive histogram equalization (CLAHE) [38] is applied to the cropped grayscale facial images. CLAHE enhances local contrast while limiting noise amplification, improving the model’s robustness to illumination differences. To enforce a square aspect ratio suitable for CNN input, the bounding box is adjusted based on the relative dimensions of height and width. Specifically, if the height exceeds the width, the horizontal boundaries are symmetrically extended; conversely, if the width is greater, the vertical boundaries are expanded. This adjustment ensures that the cropped facial region forms a square while preserving the aspect ratio of the face. As the final preprocessing step, all facial images are resized to a fixed dimension of 48×48 pixels to ensure consistent input size for subsequent CNN-based age estimation.
The entire preprocessing pipeline, including face alignment, contrast enhancement, and resizing, is visualized in Fig. 3 to enhance reproducibility and understanding of each transformation step applied to the facial images.
To mitigate the issue of data imbalance in facial age estimation, particularly for underrepresented age groups, we employ a data augmentation strategy based on a CAE. The CAE consists of an encoder and a decoder. The encoder transforms a preprocessed grayscale facial image I ∈ ℝ48×48 into a compact latent representation z ∈ ℝd through a series of convolutional layers and non-linear activations, where d denotes the dimensionality of the latent space (d = 32 in our implementation). This encoding process is formally defined as:
where fencoder(·) denotes the encoder network. The decoder reconstructs the original image from the latent code using transposed convolutional layers:
where fdecoder(·) is the decoder network and is the reconstructed output.
Unlike GANs, which rely on adversarial training between a generator and a discriminator, or VAEs, which impose a probabilistic prior over the latent space and introduce sampling variability, our CAE is optimized solely using a reconstruction loss. This approach ensures stable training dynamics and better preservation of high-frequency details crucial for capturing age-specific facial features. To this end, the CAE is trained to minimize the pixel-wise reconstruction error between the original and reconstructed facial images, encouraging the encoder–decoder architecture to learn compact and meaningful latent representations that retain age-relevant information.
Let denote a set of N preprocessed grayscale facial images, and let represent the corresponding reconstructions generated by the CAE. The reconstruction loss is defined as the mean squared error (MSE) between the original and reconstructed images:
where denotes the squared Euclidean distance. This loss function ensures that the reconstructed images closely resemble the input images in pixel space, thereby promoting the retention of fine-grained visual characteristics important for age estimation. To reflect the diversity of facial features across age ranges, we train a separate CAE for each five-year age interval, covering the full age range present in typical facial age estimation datasets.
Once the CAE is trained, its encoder and decoder can be leveraged to generate synthetic facial images for data augmentation. Specifically, to create an augmented sample, two images Ia and Ib are randomly selected from the same age group. Their corresponding latent representations, za and zb, are obtained via the encoder:
A new latent vector zaug is then generated using a convex combination of the two latent vectors:
where γ denotes the interpolation weight. To maintain sufficient variation while ensuring balanced contribution from both inputs, γ is sampled from a continuous uniform distribution U(0,1) for each augmented sample. The decoder then transforms zaug into a new facial image , which resembles a plausible face that lies in-between the two original samples in the latent space:
To assign an appropriate label to the synthesized image, the corresponding age value is computed as a convex combination of the original age labels:
where ta and tb denote the ground-truth ages associated with the two selected original images used for interpolation. This interpolation strategy not only generates plausible intermediate facial appearances but also produces corresponding age labels that lie within the convex hull of the original values, preserving label consistency for regression training.
This augmentation procedure is repeated until a sufficient number of samples is generated for each underrepresented age group. The generated images preserve realistic facial attributes and offer continuous age labels, enhancing the training diversity of the CNN-based age estimation model. By leveraging latent space interpolation, the proposed CAE-based method provides a controllable and effective solution for data augmentation in regression-based facial age prediction.
Fig. 4 shows the architecture of the CAE employed in this study. This CAE architecture is adopted from our previous work on facial emotion recognition, where it was demonstrated to be effective for learning compact and expressive facial representations through reconstruction objectives [39]. As shown in the figure, the CAE architecture is designed to process 48×48 grayscale facial images and encode them into a 32-dimensional latent vector z ∈ ℝ32. The encoder comprises four convolutional layers:
-
Conv Layer 1: 32 filters, kernel size 3×3, stride 1, padding “same”, followed by rectified linear unit (ReLU) activation.
-
Conv Layer 2: 64 filters, kernel size 3×3, stride 2, padding “same”, followed by ReLU activation.
-
Conv Layer 3: 64 filters, kernel size 3×3, stride 2, padding “same”, followed by ReLU activation.
-
Conv Layer 4: 64 filters, kernel size 3×3, stride 1, padding “same”, followed by ReLU activation.
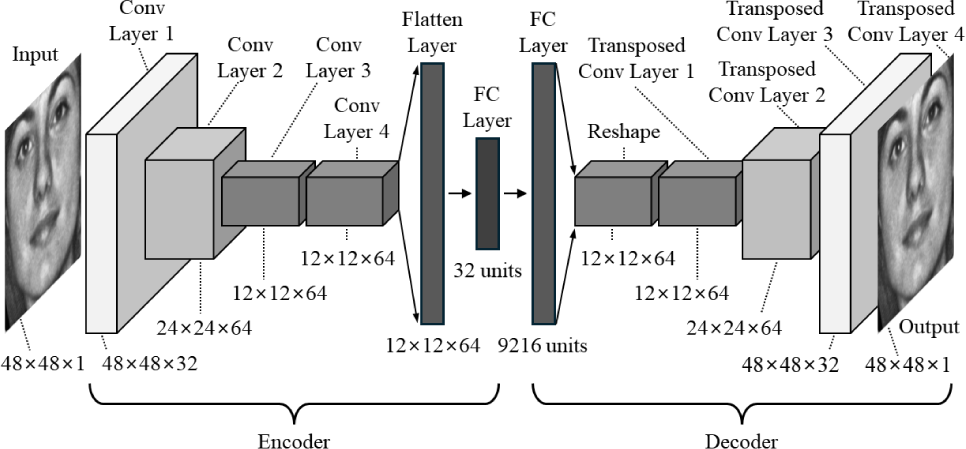
The output is flattened and passed through a fully connected (FC) layer with 32 units, forming the latent representation z.
The decoder mirrors this structure in reverse using transposed convolution layers:
-
FC Layer: Input z ∈ ℝ32 is mapped to 9,216 units, reshaped into a 12×12×64 tensor.
-
Transposed Conv Layer 1: 64 filters, kernel size 3×3, stride 1, padding “same”, with ReLU.
-
Transposed Conv Layer 2: 64 filters, kernel size 3×3, stride 2, padding “same”, with ReLU.
-
Transposed Conv Layer 3: 32 filters, kernel size 3×3, stride 2, padding “same”, with ReLU.
-
Transposed Conv Layer 4: 1 filter, kernel size 3×3, stride 1, padding “same”, with ReLU, producing the reconstructed image .
The network is trained to minimize the MSE defined in (7). Optimization is performed using the Adam optimizer with a default learning rate of 0.001. To accommodate the varying number of training samples across different age groups, the batch size is not fixed but adaptively chosen from {2, 4, 8, 16, 32} based on the size of each group. Smaller batch sizes are used for age groups with limited data, while larger batch sizes are applied to groups with more abundant samples. Training is performed for a fixed number of epochs, and early stopping is applied based on validation loss to prevent overfitting.
The complete process of the proposed CAE-based data augmentation strategy is illustrated in Fig. 5. As shown in the figure, the training phase involves learning a latent representation of facial features using a CAE trained to minimize the reconstruction loss. During the augmentation phase, two images from the same age group are selected, their latent vectors are interpolated, and the decoder generates a new synthetic image that reflects intermediate characteristics. The corresponding continuous age label is assigned using the same convex combination of the original labels. This approach ensures that the generated data remain semantically valid while enhancing the diversity and density of training samples in underrepresented age intervals.
IV. EXPERIMENTAL RESULTS
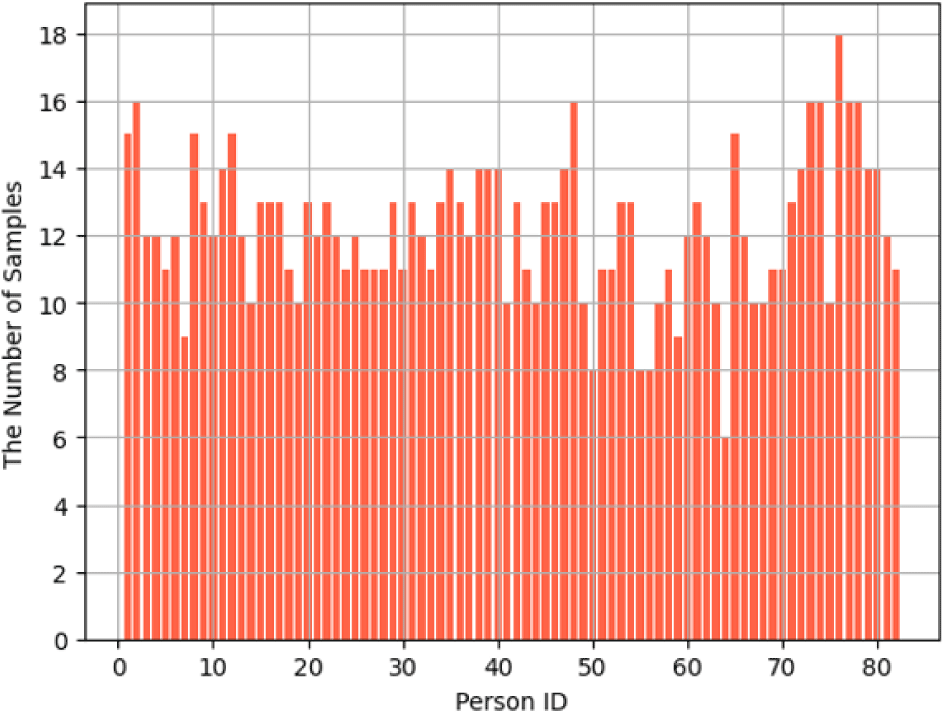
To evaluate the performance of the proposed method, experiments were conducted using the FG-NET aging database [4], a widely adopted benchmark dataset for facial age estimation tasks. The FG-NET dataset consists of 1,002 face images from 82 subjects, with ages ranging from 0 to 69 years. Each subject is represented by multiple images captured at different ages, with an average of approximately 12 age-separated images per person, as shown in Fig. 6. The images in FG-NET exhibit considerable diversity in terms of resolution, lighting conditions, facial expressions, and occlusions such as eyeglasses and facial hair, reflecting the variability typically encountered in real-world scenarios. Each image in the dataset is annotated with 68 facial landmark points, enabling detailed shape analysis and alignment operations. In our work, these landmarks are used to preprocess the face images prior to training and augmentation.
To ensure fair and standardized evaluation, we adopt the LOPO cross-validation protocol, which is the de facto standard for experiments conducted on the facial age estimation task. In LOPO, for each of the 82 subjects, the model is trained on the images of the remaining 81 subjects and tested on the held-out subject. This process is repeated until each subject has been used as the test subject once, and the final performance is reported as the average across all trials. This person-independent evaluation strategy effectively assesses the model’s generalizability across unseen individuals, which is critical for real-world applicability.
During each fold of the LOPO cross-validation, the proposed CAE-based data augmentation strategy is applied to the facial images of the 81 subjects to generate synthetic samples for age groups with relatively limited data. To address limitations in data availability and facilitate robust training of separate CAE models per age group, the FG-NET dataset is partitioned into 14 age groups, each spanning five years: 0–4, 5–9, 10–14, 15–19, 20–24, 25–29, 30–34, 35–39, 40–44, 45–49, 50–54, 55–59, 60–64, and 65–69.
This grouping strategy is motivated by two main factors. First, the FG-NET dataset contains several age values (e.g., 56, 57, 59, 64, 65, 66, and 68) for which no facial images are available, making it infeasible to apply age-specific augmentation or model training. Second, the number of available facial images decreases with increasing age, particularly in the older age ranges, as illustrated in Fig. 1. Grouping ages into five-year intervals alleviates the sparsity of training data within individual ages and facilitates more stable and effective learning of the CAE models. The number of facial images contained in each age group is summarized in Table 1.
| Age group | Age intervals | No. of samples |
|---|---|---|
| 1 | 0–4 | 193 |
| 2 | 5–9 | 178 |
| 3 | 10–14 | 174 |
| 4 | 15–19 | 165 |
| 5 | 20–24 | 84 |
| 6 | 25–29 | 60 |
| 7 | 30–34 | 46 |
| 8 | 35–39 | 33 |
| 9 | 40–44 | 28 |
| 10 | 45–49 | 18 |
| 11 | 50–54 | 12 |
| 12 | 55–59 | 3 |
| 13 | 60–64 | 6 |
| 14 | 65–69 | 2 |
As illustrated in Fig. 1 and Table 1, the FG-NET dataset exhibits a significant imbalance in the distribution of samples across age groups. While there is an abundance of samples for younger individuals particularly those under age 20 the number of samples diminishes considerably in older age ranges. To mitigate this imbalance, we employ the proposed CAE-based data augmentation strategy. During each fold of the LOPO cross-validation, we first identify the age group with the largest number of original training samples. For every other age group with fewer samples, synthetic images are generated using the CAE until their sample count matches that of the majority group. Each synthetic image is created by interpolating the latent vectors of two randomly selected training samples from the same age group, with the interpolation weight γ sampled from a continuous uniform distribution U(0,1). Since this procedure is repeated per fold based on the training data composition, the number of generated samples varies dynamically across cross-validation splits. For this reason, we do not provide fixed counts of augmented samples in Table 1.
Fig. 7 presents representative examples of the synthetic facial images generated using the proposed CAE-based augmentation strategy. For each five-year age group, the CAE is trained separately and used to produce synthetic samples by interpolating the latent vectors of two original training images from the same group. As shown in the figure, the generated images retain realistic facial features and smooth age transitions, validating the capability of the proposed method to generate high-quality and age-consistent samples even in age ranges with sparse data. These synthesized images contribute to balancing the age distribution of training data, which is particularly critical for the older age groups.

To quantify the accuracy of age estimation, we adopt the mean absolute error (MAE), a widely used regression metric. Let M be the total number of test samples. For each test image k ∈ {1,2,…, M}, let t(k) denote the ground-truth age and t̃(k) denote the predicted age. The MAE is then defined as
A lower MAE indicates more accurate age predictions, with zero representing a perfect prediction. By adhering to the LOPO protocol and utilizing established evaluation metric, our experimental setup provides a rigorous framework for assessing the effectiveness of the proposed CAE-based data augmentation strategy in facial age estimation.
To evaluate the effectiveness of the proposed CAE-based data augmentation strategy, we conducted experiments using a variety of widely used CNN architectures: LeNet-5 [40], AlexNet [41], VGG16, VGG19 [42], ResNet50V2 [43], and MobileNetV2 [44]. These models have been extensively applied in computer vision tasks and offer varying levels of depth and complexity, making them suitable benchmarks for assessing generalizability. All networks were trained using the MSE loss function defined in (7), with a batch size of 32. The Adam optimizer with a learning rate of 0.001 was employed to update network parameters, and early stopping was applied to prevent overfitting by monitoring the validation loss.
For each CNN model, we performed LOPO cross-validation using the FG-NET dataset. The aggregated performance results across all folds are presented in Table 2. These results illustrate the performance improvements achieved through the integration of the proposed data augmentation method across different network architectures.
As summarized in the table, we evaluated the effectiveness of the proposed CAE-based data augmentation strategy across six representative CNN architectures: LeNet-5, AlexNet, VGG16, VGG19, ResNet50V2, and MobileNetV2. These models were chosen to cover a range of architectural complexities, from shallow to deep, and lightweight designs. To investigate the impact of weight initialization on age estimation performance, we considered two training settings: random initialization and transfer learning via pre-training on the ImageNet dataset.
For LeNet-5 and AlexNet, all network parameters were initialized randomly, and the models were trained from scratch using the training data generated for each fold in the LOPO cross-validation. These relatively shallow networks served as baselines for evaluating the general benefit of data augmentation in low-capacity models. For the deeper architectures VGG16, VGG19, ResNet50V2, and MobileNetV2 we evaluated two variants: (1) random initialization and (2) fine-tuning from pre-trained ImageNet weights. In the fine-tuning setting, all convolutional layers were initialized with weights pre-trained on ImageNet, and only the FC layers were modified. Specifically, the final classification layer was replaced with a regression head consisting of a single neuron to predict continuous age values. The entire network was then fine-tuned end-to-end using our training protocol under the LOPO scheme.
The results in Table 2 demonstrate the consistent benefit of the proposed CAE-based augmentation across all configurations. In the case of LeNet-5 and AlexNet, which relied solely on randomly initialized weights, the MAE decreased from 7.40 to 6.93 and from 6.56 to 5.99, respectively, showing that even shallow models benefit significantly from the enriched data distribution. When examining the deeper networks under random initialization, VGG16, VGG19, ResNet50V2, and MobileNetV2 also showed noticeable improvements (e.g., ResNet50V2 improved from 3.11 to 2.99). While transfer learning from large-scale datasets such as ImageNet often yields performance gains in general visual tasks, its effectiveness in facial age estimation can be limited due to the domain mismatch. ImageNet contains few or no facial images and lacks the fine-grained age-related facial variations required for accurate regression. Consequently, in our experiments, CNNs fine-tuned from ImageNet-pretrained weights (e.g., VGG16, VGG19, ResNet50V2, MobileNetV2) did not outperform their counterparts trained from scratch. For instance, MobileNetV2 achieved an MAE of 2.77 with random initialization, which was slightly better than its ImageNet-pretrained version (2.89). A similar trend was observed for ResNet50V2, where the randomly initialized model outperformed the fine-tuned version.
These findings suggest that, for age estimation, pre-training on a task-specific or domain-relevant dataset would be more beneficial than general-purpose pre-training. Moreover, regardless of the initialization strategy, the proposed CAE-based data augmentation consistently improved model performance by enriching the training data for underrepresented age groups, thereby reducing data imbalance and enhancing generalization in LOPO evaluation.
While transfer learning from large-scale datasets such as ImageNet often yields performance gains in general visual tasks, its effectiveness in facial age estimation can be limited due to two primary factors. First, there exists a significant domain mismatch: ImageNet predominantly comprises object-centric and scene-level images, with few or no human facial images. Consequently, the features learned during pre-training are not well-suited for capturing the subtle age-specific variations in facial appearance required for regression-based age estimation. Second, the relatively small size of the FG-NET dataset further constrains the potential of transfer learning. With only a few hundred training samples per fold in LOPO evaluation, the fine-tuning process may not sufficiently adapt the high-capacity pretrained networks to the facial domain, leading to overfitting or suboptimal convergence. These observations align with our experimental findings, where randomly initialized networks consistently outperformed their ImageNet-pretrained counterparts, particularly when paired with our task-specific data augmentation.
Table 3 presents a comparative evaluation of facial age estimation models on the FG-NET dataset under the widely adopted LOPO cross-validation protocol. The table aggregates MAE values reported in prior studies that specifically adopted the LOPO setting, thereby ensuring a fair and consistent performance comparison. As shown, most existing methods achieve MAE values ranging from approximately 3.05 to 6.22 years, with performance generally improving in more recent studies that incorporate deep learning architectures or domain adaptation techniques.
| Method | MAE |
|---|---|
| Aging Pattern Subspace (AGES) Algorithm [45] | 6.22 |
| Relevance Vector Machine (RVM) [46] | 6.2 |
| Regression with Uncertain Nonnegative Labels [47] | 5.78 |
| Improved Iterative Scaling (ISS) Algorithm [48] | 5.77 |
| Ranking with Uncertain Labels [49] | 5.33 |
| Synchronized Submanifold Embedding (SSE) [50] | 5.21 |
| LBP Kernel Density Estimate [51] | 5.09 |
| Locally Adjusted Robust Regressor (LARR) [52] | 5.07 |
| Probabilistic Fusion Approach (PFA) [53] | 4.97 |
| Ranking-KNN [54] | 4.97 |
| Rank-based Age Value Estimation [55] | 4.89 |
| Ordinal Discriminative Features (PLO) [56] | 4.82 |
| Biologically Inspired Features (BIF) [57] | 4.77 |
| Deep Expectation (DEX) [58] | 4.63 |
| Component and Holistic BIF [59] | 4.6 |
| Ordinal Hyperplane Ranking (OHRank) [60] | 4.48 |
| Biologically Inspired Active Appearance Model [61] | 4.18 |
| Mean-Variance Loss [62] | 4.1 |
| Deep Regression Forests (DRFs) [24] | 3.85 |
| Deep Hybrid-Aligned Architecture (DHAA) [63] | 3.72 |
| Adaptive Mean-Residue Loss [64] | 3.61 |
| Extended BIF (EBIF) [65] | 3.17 |
| Deep Random Forests [66] | 3.05 |
| MobileNetV2 (Random Init.)+Proposed CAE-DA | 2.77 |
Among these, the method by [66] achieves one of the strongest performances with an MAE of 3.05. However, it is noteworthy that even the most competitive prior approaches fail to surpass the 3.0 MAE. The proposed approach, leveraging the CAE-based data augmentation strategy and MobileNetV2 with randomly initialized weights, yields a new state-of-the-art result of 2.77 MAE. This performance not only surpasses all listed methods but also demonstrates the robustness and effectiveness of the proposed augmentation strategy in alleviating data imbalance and improving generalization to unseen individuals a critical requirement under the LOPO protocol. Furthermore, the superior performance is achieved without relying on pre-training with large-scale datasets like ImageNet, suggesting that the model benefits more from task-specific data augmentation than from generic transfer learning. This reinforces the notion that targeted augmentation especially in underrepresented age groups can be more beneficial than domain transfer in age estimation tasks.
V. DISCUSSION
While the proposed CAE-based data augmentation method demonstrates substantial improvements in facial age estimation performance, it is important to acknowledge several limitations inherent to the current design.
First, the effectiveness of the CAE model in generating realistic facial images is highly dependent on the consistency of pose and alignment in the training data. When trained on well-aligned frontal facial images, the CAE reliably reconstructs visually coherent outputs. However, if images with varying poses and orientations are included without proper alignment, the decoder may generate unrealistic faces or structural artifacts due to the entangled representation of pose and identity in the latent space. To mitigate this, we apply a robust face alignment preprocessing step based on facial landmark detection and rotation normalization, as illustrated in Fig. 3. This step helps standardize facial orientation and significantly improves the quality of the generated images.
Second, the latent space interpolation used for synthetic image generation assumes a linear manifold between two encoded representations. While this assumption works reasonably well in practice, it may not capture more complex nonlinear transformations between facial expressions, identity traits, or age progression paths. As a result, the diversity of synthesized samples may be limited, and subtle semantic shifts could be underrepresented.
Finally, since separate CAE models are trained per age group, the quality and stability of each model can be affected by the amount of available data within that group. In extremely underrepresented age intervals, the learned reconstructions may lack sufficient richness or generalizability, despite the use of adaptive batch sizes and regularization.
We consider these limitations to be promising avenues for future research, such as incorporating pose-invariant representation learning, nonlinear interpolation strategies (e.g., spherical or geodesic interpolation), or more expressive generative backbones [67-100].
VI. CONCLUSION
This paper presented a CAE-based data augmentation framework for facial age estimation, targeting the issue of data imbalance inherent in real-world age datasets. By interpolating between latent representations of facial images, our method generates age-consistent synthetic samples that enrich underrepresented age groups, particularly in the higher age ranges. To maintain semantic fidelity in augmented data, a convex combination of both the latent vectors and corresponding age labels was employed.
We validated the effectiveness of our approach through extensive experiments on the FG-NET dataset using the LOPO cross-validation protocol. The proposed augmentation strategy consistently improved performance across six different CNN architectures. Among them, MobileNetV2 with randomly initialized weights achieved the lowest MAE of 2.77, surpassing previously reported methods and demonstrating that transfer learning from unrelated domains like ImageNet is not always beneficial for fine-grained facial analysis tasks such as age estimation.
Our findings underscore the critical role of tailored data augmentation strategies in alleviating data imbalance and enhancing model generalization in facial analysis tasks. Beyond its performance on FG-NET, the proposed framework is inherently scalable and can be extended to larger, more diverse datasets. Because the method does not depend on domain-specific priors and requires only paired facial images and age labels, it can be applied to datasets with broader demographic distributions, varied poses, or higher resolutions.
Future research will explore the integration of this framework into other facial attribute estimation tasks (e.g., gender or ethnicity) and evaluate its performance on more complex benchmarks. In addition, incorporating adversarial regularization or contrastive objectives into the training process may further improve the realism and diversity of the synthesized faces.

