Asymmetric Key Construction Based on Palmprint Hash Coding

In 2023, Yang et al. [11] proposed the Competitive Palmprint Hash Network (CCNet), which captures unique texture features through learnable Gabor filters and integrates a comprehensive competition mechanism. Subsequently, Yang et al. [12] optimized the position of the hash layer based on CCNet, placing it after the fully connected layer to construct a new Hash Competition Network, further enhancing template protection capabilities. In 2024, Khan et al. [13] integrated chaotic sequences as weights into the neuron activation layer, supporting dynamic control to generate diverse palmprint feature templates. Chen et al. [14] proposed an enhanced multi-task learning framework that jointly optimizes identity recognition, soft biometric attribute classification, and hash branches, achieving template compression and matching acceleration while maintaining recognition performance. In 2025, Liu et al. [15] proposed a distillation-driven deep hash retrieval scheme, realizing lightweight and efficient retrieval and recognition with short bits in palmprint and finger vein recognition, verifying the feasibility and scalability of binary hash templates in hand biometrics. Liao et al. [16] developed a general framework suitable for texture-based tasks based on the second-order texture feature extraction method. Sai Kishore et al. [17] conducted a performance analysis of distillation-based hash palmprint recognition schemes, compressing deep models into lightweight hash encoders through knowledge distillation, and simultaneously improving recognition accuracy and inference speed in short-bit matching scenarios.

In the field of biometric cryptosystems, in 2022, Wu et al. [18] used deep hash coding as palmprint templates to construct a fuzzy commitment cryptosystem, and proposed a bit discriminative energy compression algorithm to balance the improvement of hash code accuracy and length compression. Suresh et al. [2] collected features through a fingerprint recognition system and input them into a random number generator to generate RSA public and private keys. In 2023, Barman et al. [19] adopted fuzzy commitment technology to securely store biometric data on remote servers, whose security was confirmed by two protocol verification tools. Lin et al. [20] proposed an error correction-based iris recognition scheme, selecting LDPC codes as error-correcting codes to achieve soft and reliable extraction. Shahreza et al. [21] processed extracted features through a user-specific random weighted Multilayer Perceptron (MLP) and binarized the output to generate protected biometric templates.

In 2024, Jide et al. [22] generated 256-bit private keys from binary features of fingerprint images, generated public keys using the ECDSA algorithm, and applied them to voting procedures. Cao et al. [23] proposed a fixed-length ordered extraction method fusing point features and direction features, realizing efficient and secure palmprint template protection through index maximization transformation. Tran et al. [24] designed a multi-factor fuzzy extractor for key generation and reconstruction, and constructed a new multi-factor authentication key exchange protocol to enhance system security and key regeneration capabilities. In 2025, Yirga et al. [25] fused deep features of faces and finger veins, combined with fuzzy extractors to achieve reproducible key generation, and published stab-ility and security evaluation indicators. Geißner et al. [26] proposed a multi-finger deep fuzzy commitment scheme, improving key regeneration stability and increasing attack difficulty through multi-sample aggregation. Almola et al. [27] proposed a fingerprint-based key generation system combined with deep learning, using dual CNNs to be responsible for identity verification and feature extraction respectively, enhancing key randomness through particle swarm optimization, and supporting engineering implementation of real-time derivation.

Existing research still faces key technical bottlenecks: most palmprint feature encryption algorithms, in pursuit of high security and recognition accuracy, often rely on complex network architectures. This leads to numerous matrix computations during the encryption process, resulting in high time complexity. The problem is particularly prominent in applications under resource-constrained scenarios. Therefore, there is still a lack of a palmprint feature encryption algorithm that can balance encryption security, feature matching accuracy, and engineering practicality with low time complexity.

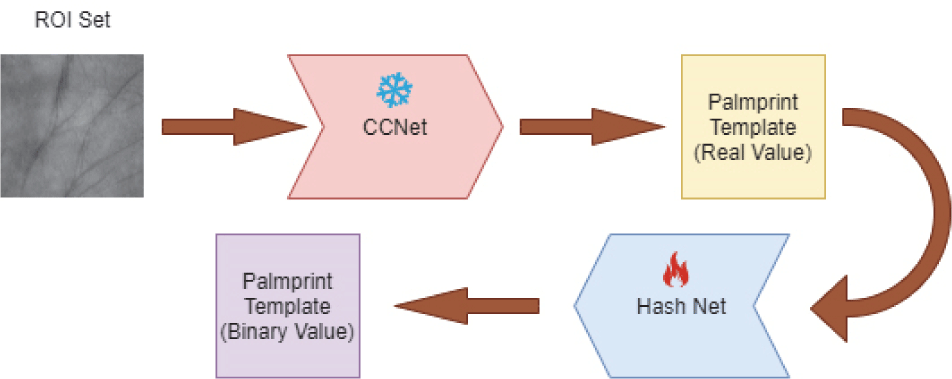
To address the problem that the high-dimensional output of current feature extraction networks makes it difficult to maintain high accuracy while reducing dimensionality, we have specifically designed a residual hash module to compress high-dimensional palmprint features. Benefiting from the high discriminability of the CCNet [11], this paper adopts it as the backbone network to extract original palmprint features. As shown in Fig. 1, the palmprint ROI generates 2048-dimensional real-valued features after passing through the trained feature extraction network. These features then go through three fully connected layers to further extract the relationships between them, with ReLU activation functions used between the fully connected layers and a Tanh activation function employed in the final hash layer to simulate binary output. The hash module can be expressed as:

Fig. 1. Hash Network Framework.

Download Original Figure

Among them, x_i∈R^N denotes the high-dimensional feature vector of a specific palmprint, f(·) represents the mapping function, and L stands for the length of the output binary code.

To ensure the inter-class discriminability and bit randomness of the output binary codes during the training of the mapping network, we adopt a Cryptographically Secure Pseudo-Random Number Generator (CSPRNG) to generate high-entropy random binary codes (SPC), which serve as class centers. To maximize the separation of these class centers and further strengthen the aforementioned design objectives, we additionally set a threshold T as the minimum Hamming distance between different SPCs. Specifically, after being mapped to the Hamming space, the hash codes of the same class gather within a Hamming sphere centered at the corresponding class center with a specific radius as the boundary, ensuring high similarity among intra-class hash codes. For the class centers of different classes, we impose strict constraints to ensure their minimum Hamming distance d ≥ T thereby achieving effective inter-class separation.

Loss Function: In the training scenario of our mapping network, the ground truth is regarded as the class center represented by the high-entropy random binary codes generated by CSPRNG, while the predicted value refers to the hash code actually generated by the network. By minimizing the L2 loss, we can drive the generated hash codes to be as close as possible to the class center of their respective classes. The L2 loss is defined as follows:

Y_i,H_i denote the output hash code of the mapping network and the class center binary code, respectively, and N represents the batch size. To prevent network overfitting, we also add a dropout layer to the fully connected layer of the last layer, with the dropout parameter set to 0.5.

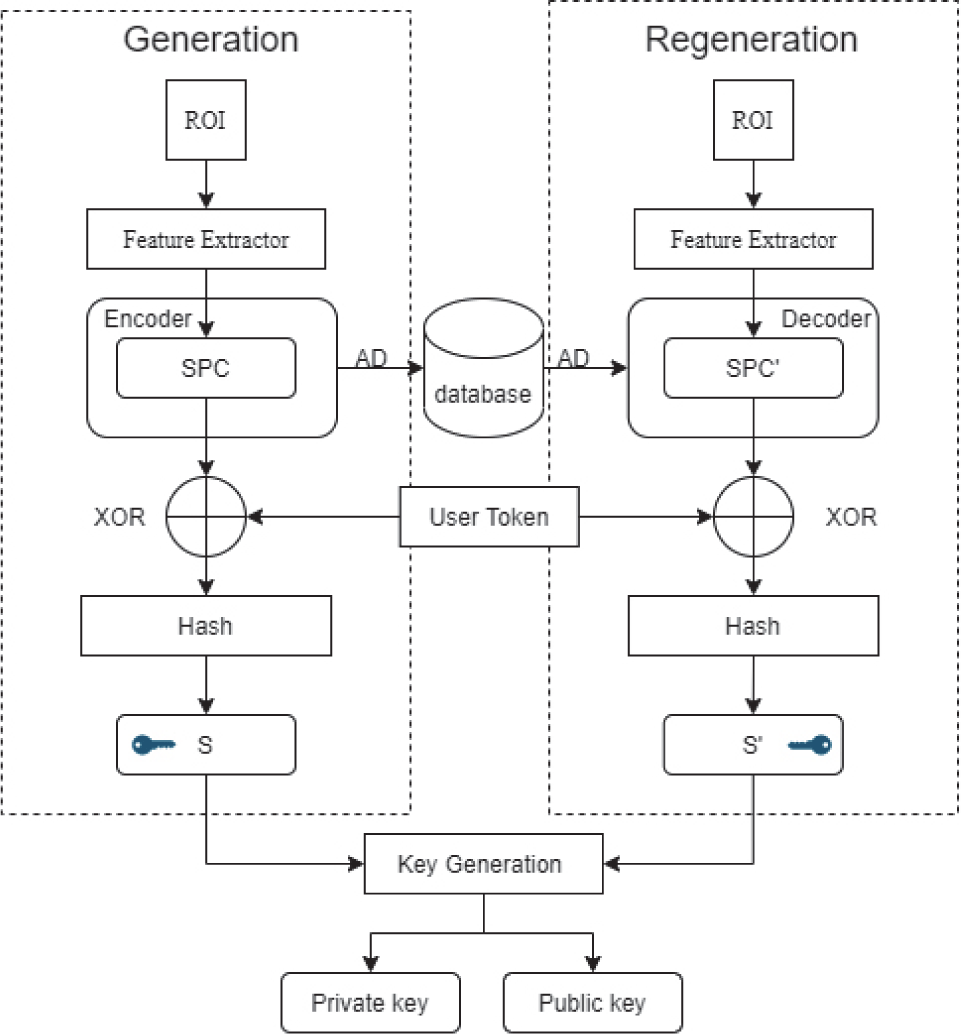
The framework of the entire algorithm is illustrated in Fig. 2, comprising two phases: Key generation and Key regeneration. During enrollment, the user provides a palm-print image to generate the feature vector SPC. After the SPC undergoes the error-correcting coding construction algorithm, auxiliary data (AD) is generated, which is used for decoding during subsequent key regeneration. To further ensure the security of the key, the user needs to provide a Token to encrypt the original feature vector, defending against credential stuffing attacks. Finally, a one-way hash encryption algorithm is adopted to ensure that the generated key seed S cannot be reversed to recover the user’s original feature vector even if compromised. Eventually, S is input into the asymmetric key generator to generate the public key and private key. During the key regeneration phase, the feature vector generated by decoding the AD stored in the database is used to recover the SPC from enrollment, and the remaining processes are consistent with those in the generation phase.

Fig. 2. Asymmetric key generation framework.

Download Original Figure

The error-correcting coding algorithm adopts BCH codes. Three parameters need to be specified when constructing the error-correcting coding algorithm: code length n, information bit length k, and number of correctable bits t. Typically, n = 2^m − 1, m ∈ ℤ⁺, k ≤ n − 2t. The error-correcting capability of BCH codes is determined by the design parameter t, which can theoretically correct up to t random errors. Its error-correcting capability satisfies the relationship with the minimum Hamming distance: d_min ≥ 2t + 1. To maximize the error-correcting capability of BCH codes and minimize redundancy, the hash mapping network presented in Section 3.1 is used to generate fixed-length SPCs suitable for BCH coding. Table 1 provides reference parameters for n, k, t, and SPC length. During user enrollment, the construction algorithm is invoked to generate parity bits, which are then stored in the database. During key regeneration, the BCH decoding algorithm is utilized.

To ensure that the key seed S does not reveal any information about the original palmprint, a User Token is used to perform an XOR operation on it. The User Token has the same length as the codeword encoded by the BCH algorithm. The User Token needs to be generated from a password provided by the user, and the provided password must comply with the NIST [28] protocol. The PBKDF (Password-Based Key Derivation Function) algorithm is adopted to perform multiple iterations and salting calculations on the input password, ultimately generating the User Token.

Untransformed palmprint feature templates are vulnerable to credential stuffing attacks and reconstruction attacks. [29] Therefore, we adopt a hash algorithm to perform one-way mapping on the generated palmprint feature templates, yielding the key seed S or S’.

The key seed S is split into S1 and S2, which are then input into a Pseudorandom Number Generator (PRNG) to generate two large integers. To ensure the security of the RSA key, the generated large integers are set to 1,024 bits in length, and the last bit is set to 1 to ensure they are odd numbers.

After generating the two large integers, an efficient probabilistic algorithm (Miller-Rabin Primality Test) is adopted to check if they are large primes. If not, the large integer is incremented by 2 and the check is repeated. After iterative verification, two large primes p and q are obtained.

At this point, based on the aforementioned large primes p and q, the RSA asymmetric key pair can be constructed. First, the modulus n is calculated, which is the product of the two large primes and serves as a common component of both the public key and the private key:

Next, Euler’s totient function ϕ(n) is calculated. This function describes the number of positive integers coprime with n and serves as a key parameter for key generation:

Subsequently, an integer e is selected as the public key exponent, and its selection must satisfy two conditions:

Finally, the private key exponent d is calculated, which is the modular inverse of the public key exponent e under modulo ϕ(n). This means that d must satisfy the following congruence equation:

The final resulting key pair is: public key (n,e) and private key (d,n).

The proposed method is evaluated on two public palmprint datasets: PolyU [30] and Tongji [31]. Among them, the Tongji dataset consists of palmprint data collected by a non-contact device, while the PolyU dataset is collected through contact-based acquisition. Fig. 3 shows the ROI example for PolyU and Tongji.

Fig. 3. The ROI image of PolyU and Tongji.

Download Original Figure

The hash network is implemented using PyTorch. From the state-of-the-art (SOTA) palmprint recognition models based on deep learning, CCNet is selected as the backbone network for palmprint feature extraction. CCNet is trained with the parameter settings as described in the original paper. For all datasets, the number of training epochs is set to 1,000 and the ratio of the training set to the test set is 1:1. The residual mapping network is trained with 500 epochs, using the same training and test sets as CCNet. The Adam optimizer is adopted with a learning rate of 0.001.

The hardware used in this study includes an Intel(R) Xeon(R) Platinum 8222CL CPU @ 3.00 GHz, 64 GB of memory, and an NVIDIA GTX 3090 GPU.

The hash network proposed in Section 3.1 is used for hash mapping on two public palmprint datasets (PolyU and Tongji). Table 2 presents the Equal Error Rate (EER%) as well as the Minimum and Maximum Hamming distances for Genuine users and Imposters under different datasets and various bit lengths.

As can be seen from Table 2, the overlap of matching results between Genuine and Imposter only occurs for the 57-bit hash codes of the PolyU dataset. The Equal Error Rate (EER) is determined when the False Acceptance Rate (FAR) equals the False Rejection Rate (FRR), and the corresponding threshold is adopted as the value of parameter t for BCH code construction. If the EER is 0, the maximum Hamming distance of Genuine users is directly used as the threshold, i.e., parameter t. Table 3 presents the thresholds and recommended BCH code parameters for different datasets under various bit lengths. With a fixed information bit length k, if the threshold is less than the number of correctable bits t, it indicates that the BCH code can fully recover the original palmprint feature template without causing overlap.

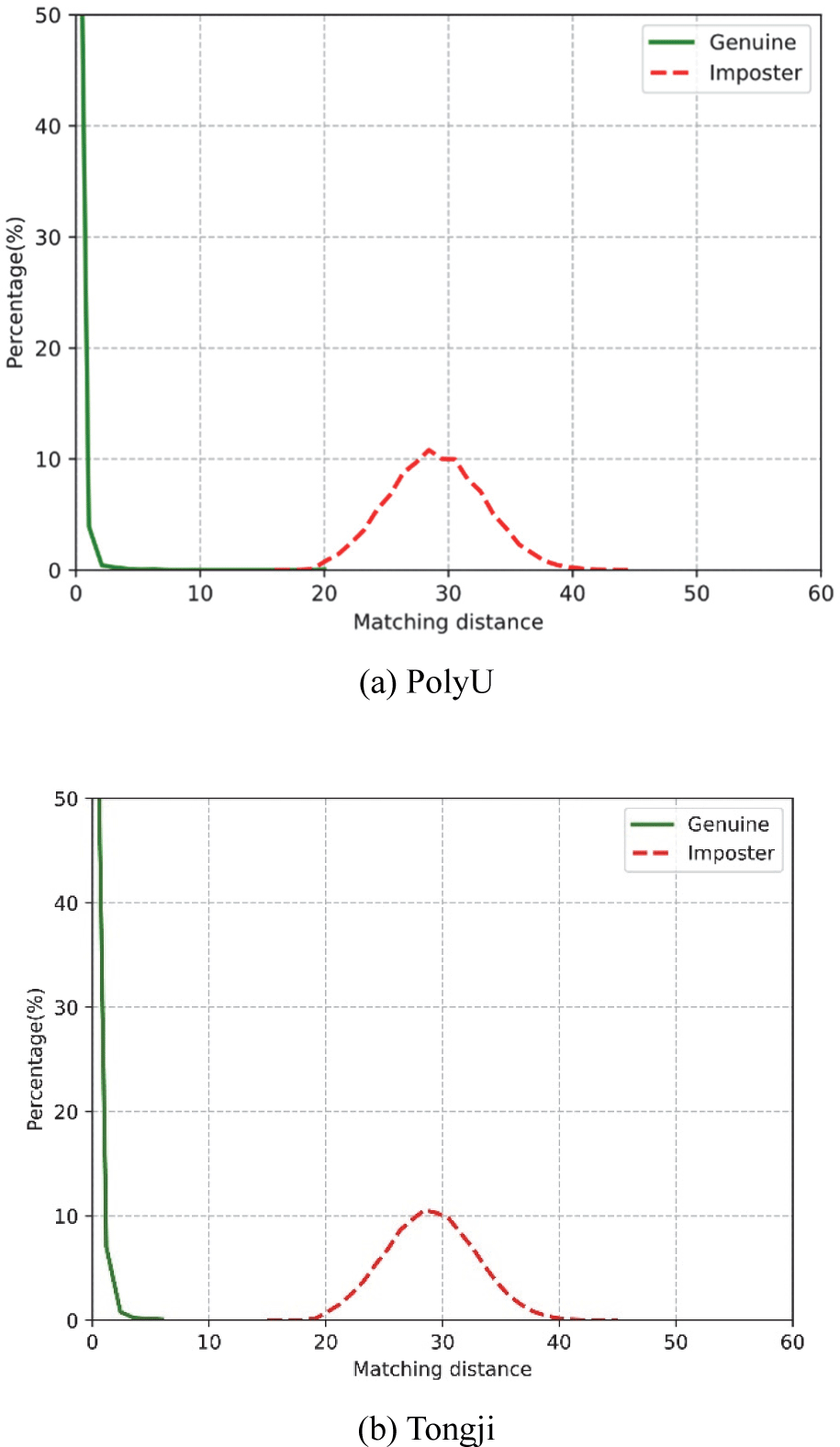
Fig. 4 presents the matching distance distribution diagram of the two datasets at a bit length of 57. It can be observed from the figure that only the PolyU dataset exhibits an overlap between Genuine (genuine samples) and Imposter (imposter samples), while the Tongji dataset is completely separated with a significant degree of separation between the two curves. This demonstrates that our method remains highly effective even at short bit lengths.

Fig. 4. The matching distance distribution of PolyU and Tongji with 57 bits length.

Download Original Figure

Only the parity bits generated during the BCH encoding process is stored in the database. These parity bits do not contain any information related to biometrics, thereby ensuring the security of the biometric template and resisting brute-force search attacks and cross-matching attacks.

In a brute-force search attack, the attacker has no knowledge of the key generation method or the auxiliary information stored in the database. To find the correct key, the number of searches required by the attacker equals the length of the generated key. If the key length is L, the number of searches for the attacker is 2^(L−1). The RSA key generated in this paper has a length of 2,048 bits, which is sufficient to resist such attacks.

In a cross-matching attack, the attacker may access the user’s palmprint features stored in other databases. Even if the attacker obtains the user’s palmprint features, they still need the user’s Token to generate the key. Without acquiring the user’s Token, the attacker remains unable to obtain the key.