I. INTRODUCTION
Now the development of vehicles was concentrated on not only improving performance, but also to protect the drivers and passengers in a vehicle in the occurrence of a traffic accident. The degree of injury to passengers in a vehicle caused by a traffic accident is reduced gradually in advantage of many safety device techniques mounted in and outside of the vehicle. But the accidents outside of a vehicle that caused by a driver’s carelessness or by road environments still have many problems, so it is required to detect the risk of a traffic accident in order to save lives [1].
Most of the studies relating to human safety over the past several years have mainly concentrated on increasing the detection rate of pedestrians and automobiles on a road from a still image and framework. The ability to detect the two-wheeler is a task that human safety risibly performs but one that computers to date have been unable to perform robustly. Now, the study scope has expanded to protect vulnerable road users (VRUs) such as small automobiles [1, 2]. Because pedestrians and bicycle riders are very vulnerable road participants among VRUs, they are a hot subject for the study field in intelligent transportation system. Therefore various types of sensors are utilized for an accurate and real time detection and tracking; NIR, FIR, LIDAR, RADAR, Laser Scanner, fusion system, and etc.
Among VRUs on the road, pedestrians are the slowest while the others have the characteristics of moving speedily. Two-wheelers, different from ordinary pedestrians, are expressed with complicated shapes in combination of the rider’s dressing style, hair style, whole body attitude, forms and patterns of loading, and various types of two-wheelers, which makes the shapes even further complicated according to the viewing angle, so that it requires a stronger algorithm against changes in their shapes.
The automobile vision-based systems have mainly concentrated on recognizing pedestrians and automobiles [3]. As stated in the foregoing, detection of two-wheelers on the road is similar with that of pedestrians on road. Extracting characteristics for detecting pedestrians are classified with single characteristics, multiple characteristics, whole area characteristics, and district characteristics pursuant to the usage of extracted characteristics [4]. Especially, HOG characteristics or Improved HOG characteristics are widely utilized in the methods for recognizing pedestrians by using the automobile vision. Zhu et al. [5] applied the HOG characteristics based on variable block size to improve detection speed. Further, Watanabe et al. [6] utilized co-occurrence HOG characteristics, and Wang et al. [7] utilized HOG-LBP human detection to improve detection accuracy.
The two-wheeler includes two wheeler and person, differently a pedestrian detection. This paper define that the two-wheeler surface features are expressed as surface function to extract the feature of weighting vector. Surface curvatures can be described by surface functions which are categorized by two types of mathematics, internal and external type. Extracted two curvature vectors include the attribute of surface type feature for the a point by the combination of coefficients [8].
As we mentioned previously, two wheelers similar with not only the shape of pedestrian but also detection technique based on several features. Two wheelers consist of human and machine; usually a human is upper part and machine is lower part in the shape. It is used to calculate the correlation coefficient for cell to area. And two wheelers detection system can be adapted to the pedestrian detection algorithms for features extraction, classification, and non-maxima suppression. The solution of slow performance from dense encoding scheme and multi-level scale images is to use a boosting algorithm [9] to speed up classification process. Because of above reasons, we tried to use modified HOG algorithm to select best features and Adaboost to improve detection rate. In this study, we invented new algorithm based on correlation coefficient value which is weighted according to the limited area. More detail about general and modified correlation coefficient will describe in section 2. This paper consists of the following: Section 2 introduces basic extracting characteristics methods with curvature and correlation coefficient algorithm that can increase detection rates significantly. Section 3 states the framework and training of suggested detecting two-wheelers system. The evaluation and detailed analysis for the experimental results are summarized in section 4. Section 5 states the conclusion.
II. FEATURE EXTRACTION
Histograms of Oriented Gradients (HOGs) are feature descriptors used in computer vision and image processing for the purpose of object detection. The technique counts occurrences of gradient orientation in localized portions of an image. This method is similar to that of edge orientation histograms, scale-invariant feature transform descriptors, which uses normalized local spatial histograms as a descriptor, and shape contexts, but differs in that it is computed on a dense grid of uniformly spaced cells and uses overlapping local contrast normalization for improved accuracy.
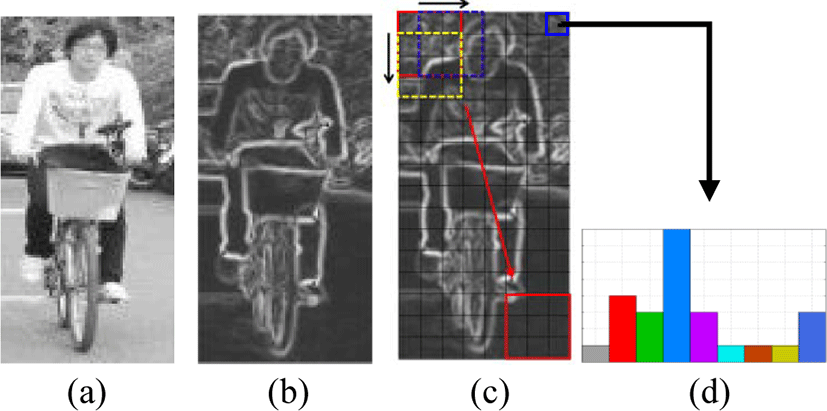
Dalal and Triggs [10] described Histogram of Oriented Gradients descriptors in the context of human detection. Their proposed method is based on evaluating well normalized local histogram of image gradient orientations in a dense grid, computed over blocks of various sizes. The main idea is that local object appearance and shape can often be characterized rather well by the distribution of local intensity gradients or edge directions. This is achieved by dividing the image into cells and for each cell a one dimension histogram of gradient directions over the pixels of the cell is calculated. Then each block in the image consists of a number of cells, as shown Fig.1.
After calculating x, y derivatives (dx and dy), the magnitude |m(x, y)| and orientation θ(x, y) of the gradient for each pixel I(x, y) is computed from
One thing to note is that, at orientation computation radian to degree method is used, which returns values between -180° and 180°. Since unsigned orientations are desired for this implementation, the orientation range of degree which is less than 0° is summed up with 180°. The next step is to compute cell histogram. Each histogram divides the gradient angle range into a predefined number of bins. In this paper, each cell, as shown Figure 1 (c) and (d), is represented by 8x8 pixel size and has 9 bins covering the orientation for [0°, 180°] interval. For each pixel’s orientation, the corresponding orientation bin is found and the orientation’s magnitude |m(x, y)| is voted to this bin. A contrast-normalization is used on the local responses to get better invariance regarding illumination, shading, etc.. To normalize the cell’s orientation histograms, it should be grouped into blocks (3x3 cells). This is done by accumulating a measure of local histogram value over the blocks and the result is then used to normalize the cells in the block. Although there are four different methods for block normalization suggested by Dalal and Triggs [10], L2-norm normalization Π is implemented using equation (5)
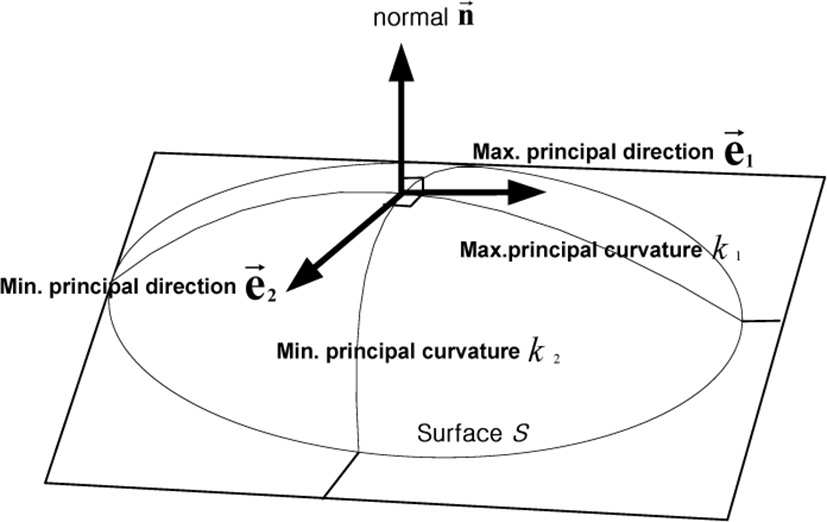
For each data point on the facial surface, the principal, Gaussian and mean curvatures are calculated and the signs of those (positive, negative and zero) are used to determine the surface type at every point[11]. The z(x, y) image represents a surface where the individual Z-values are surface depth information. The curvatures and related variables are computed for the pixel at location (0,0). Each pixel has an intensity value, a gray ton value or a depth value z(x, y). These intensity values define a surface in a three dimensional space as shown in Figure 2.
Here, x and y are the two spatial coordinates. We now closely follow the formalism introduced by Peet and Sahota [25], and specify any point on the surface by its position vector:
The first fundamental form of the surface is the expression for the element of arc length of curves on the surface which pass through the point under consideration. It is given by:
where
The second fundamental form arises from the curvature of these curves at the point of interest and in the given direction:
where
and
Casting the above expression into matrix form with;
the two fundamental forms become:
Then the curvature of the surface in the direction defined by V is given by:
Extreme values of k are given by the solution to the eigenvalue problem:
or
The second fundamental form arises from the expression of the curvature is defined as the correlation of the variation of (dx, dy) between the normal vector dn and surface displacement dR. Any surface type can be represented by the six scalar functions of E, F, G, e, f, g, resulting excellent descriptions for any surface property. The two principal curvatures to k1 and k2 gives the following expressions, respectively:
Here we have ignored the directional information related to k1 and k2, and chosen k2 to be the larger of the two. For the present work, however, this has not been done. The two quantities, k1 and k2, are invariant under rigid motions of the surface. This is a desirable property for us since the cell nuclei have no predefined orientation on the slide (the x – y plane).
The Gaussian curvature K and the mean curvature M are defined by
which gives k1 and k2, the minimum and maximum curvatures, respectively. It turns out that the principal curvatures, k1 and k2, and Gaussian are best suited to the detailed characterization for the facial surface, as illustrated in Figure 2. For the simple facet model of the second order polynomial of the form, i.e. a 3 by 3 window implementation in our range images, the local region around the surface is approximated by a quadric
and the practical calculation of principal and Gaussian curvatures is extremely simple.

A coefficient of correlation or Pearson product-moment correlation coefficient (PMCC) is a numerical measure of how much one number can be expected to be influenced by changes in another. It is expressed between -1 and 1 that measure the strength of the linear relationship between two variables. A correlation coefficient of zero means that the two numbers are not related. A non-zero correlation coefficient means that the numbers are related, but unless the coefficient is either 1 or -1 there are other influences and the relationship between the two numbers is not fixed. As previously defined, even though correlation coefficient includes the negative range, because it means that two numbers are inversely correlated, we regarded the negative value as the positive value. So this (ρ) calculator uses the following:
where σcx, σcy is standard deviation for two cell, cx and cy, and C(cx, cy) is the covariance of two cells. In General, correlation coefficient is used to explain the information we calculate about the magnitude in the one cell by observing another magnitude in the cell. As shown in Figure 4, the cells of two wheelers area are showing different type of characteristic than other area, such as background or road area (bottom). Then we emphasize that our paper proposed an innovation methods based on the relation information of two cells area; upper and lower to calculate the correlation coefficients.
III. CLASSIFICATION
Adaboost is a simple learning algorithm that selects a small set of weak classifiers from a large number of potential features according to the weighted majority of classifiers. The training procedure of Adaboost is a greedy algorithm, which constructs an additive combination of weak classifier. Our boosting algorithm is basically the same as P. Viola’s algorithm [21].
Given training set: (x1, y1),…, (xn, yn)
Where xi ∈ X, yi ∈ Y = {+1,−1}
-
Initialize weights for yi = +1, −1
m: the number of positive image(two-wheeler, +1)
n: the number of negative image(non two-wheeler,-1)
-
For t=1 ··· T:
-
(a) Normalize the weights,
so that wt,i is a probability distribution of ith training image for tth weak classification
-
(b) For each feature, j, train a classifier hj which is restricted to using a single feature.
The error is evaluated with respect to wi
-
(c) Choose the classifier, ht, with the lowest error εt
-
(d) Update the weights:
Where εi = −1 if example xi is classified correctly, εi = +1 otherwise, and
-
-
Output the final hypothesis:
where αi = log(1/βt)
The final hypothesis H is a weighted majority vote of the T weak hypotheses where αt is the weight assigned to ht. Using two strong classification, in this paper suggests 2nd stage cascade method. It improves the recognition rate due to the complementary role for two feature vector of quite different type.
IV. EXPERIMENTAL RESULTS
In this study, an experiment was carried out with an ordinary user computer environment consisting of a Pentium 3.1 GHz and Visual C++ 6.0 Program and Matlab. Two-wheelers data used in the experiment includes photos taken on the street directly and others obtained from the internet randomly. An image of two-wheelers can be expressed with various angles in an automobile. For our purposes, it is hypothesized in the experiment for the following 2 cases: a two-wheeler is running in front of an automobile (rear appearance) and a two-wheeler is coming toward the automobile (front appearance). And the experiment was done for the attitude of 90 degrees and the attitude of within 60 degrees in basis of horizontal line. 2,353 pictures of normalized two-wheelers were used with a size of 128x64 from the taken photos with a size of 640x480. They were utilized by dividing training image and experimental image. Pictures of non two-wheelers were obtained by utilizing randomly extracted pictures from the photos of streets in ordinary cities. The number of non two-wheelers used in the training was equal to the number of two-wheelers, and 3,000 pictures of non two-wheelers were used in the experiment.
The experiment was carried out using HOG method which is the most widely utilized and calculated the curvature and correlation coefficient as weighting factors which is suggested in the study. A range of thresholds of -20 to 20 was utilized in classification, and confusion matrix, true positive rate (TPR) and false positive rate (FPR) were used for analyzing experimental results per angles for the methods, and ROC curves are shown in figure. 3, by applying Eq. (22) below:
where “TP” is True Positive”, “FP” is False Positive”, “TN” is True Negative and “FN” is False Negative. In Figure 5, “Moto” means motorcycle, “Bike” means bicycle, and “MB” is a mixture of motorcycles and bicycles, respectively. Also, the numerals behind each of the abbreviations “60” signifies within 60 degrees, “90” within 90 degrees, and “90-60” a mixture of 90 and 60 degrees, respectively, as well.
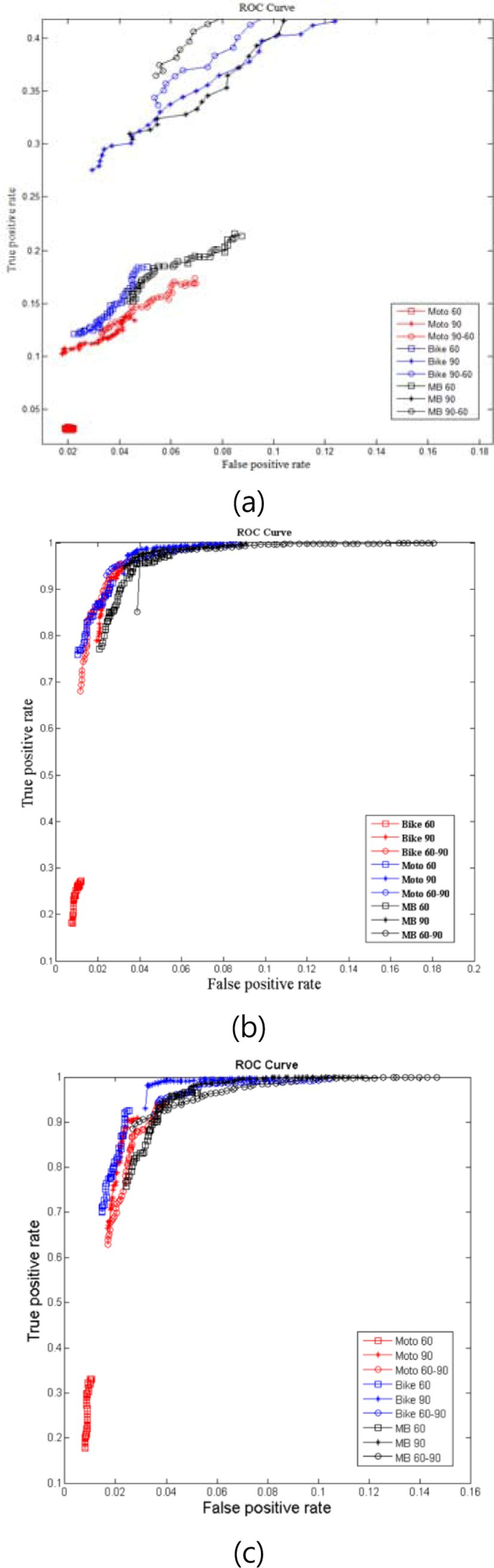
In Figure 5 (a), the ordinary HOG method, it has shown that the experiment according to “MB 90-60” has the best results among these experiments, but the recognition rate is significantly low. However, in Figure 5 (b) and (c), shows that the results of M and B experiments according to the proposed method have a higher recognition rate than other angle and types. When applied with another analytical method, as shown in Figure 5 (b) and (c), because the area of the curve of the suggested method is larger than that of the curve of the ordinary method, it is known that this system has a better performance. When proposed algorithm was applied for the other characteristic vector (curvature for kmax and kmin) method, a higher recognition rate could be obtained, and the results are listed in Figure 5 (b) and (c). The highest accuracies for each of the methods were calculated with equation (23) and the results are listed in Table 1.
As shown in Table 1, Moto (motorcycle) has higher accuracies than Bike and MB for proposed method, signifying that motorcycle has a trend of better classifying characteristics than Bike. In our opinion even if a motorcycle becomes more complicated by loading baggage at the rear or by the high loading of baggage than bicycle, our proposed algorithm improved the recognition rate than others. In the experiment of mixture of the two kinds of two-wheelers, the results of suggested method accuracies also have a higher accuracy than the existing algorithm. Because two-wheelers are composed of persons, bicycles and motorcycles have various shapes with loaded baggage. Therefore, the upper part of a waist is similar to a pedestrian but the lower part is diversified and complicated in shape, so that it becomes another field of challenge besides detection of pedestrians and automobiles for an intelligent automobile. The two-wheeler in the following means a combination of a person and a machine.
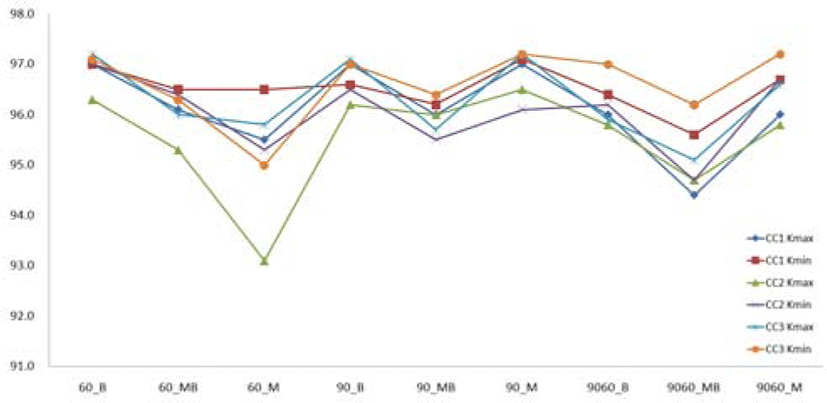
We presents the result of experiments to compare other correlation coefficient (we call CC) methods, as shown Figure 6. The CC1 was used upper and lower area to calculate the CC1 which was used the weighting factor. Using the CC2 method was compared local cell with neighbor cell. In the CC3 method using opposite target area, a local cell which is located upper area used lower area as target area and a local cell which is located lower area used upper area as target area, as shown Figure 4. In this experiment, M and B was showed very similar detection rate for each method, but CC3 method was showed higher detection rate than others for MB.
V. CONCLUSION
Accurately and efficiently two wheeler detection, riding on people, in still images is one of the most difficult works due to a variety shape of poses, as well as environmental conditions and cluttered backgrounds.
In this study, we have introduced that a novel practical implementation of the solution for weak object (vulnerable road users) on the road using projected local binary pattern. The underlying motivation of our approach originates from the observation that curvature is well presented the feature of edge and curve area.
It has been experimentally demonstrated that proposed using the curvature and correlation coefficient method as weighting value leads to better classification results than other traditional methods from ROC. Adaboost classification have comprised the main stream of research to detection two-wheelers and the results compared with existing method have been shown that it is a highly improved system performance. Additionally, among the several correlation coefficient method, the CC3 method showed higher detection rate for mixed angle (90-60) than others. For the further research, we consider including occluded region, changed objected according to the weather and night environment, and etc.