I. INTRODUCTION
Frequency-to-voltage (F/V) conversion, the ability to obtain an output voltage proportional to a frequency input, is an important basic electronic technology whose applications include speed control, flow measurement, tachometers, Doppler radar for speed sensing, and touch or sound switches [1].
Medical telemetry, which collects electrocardiograms and respiratory patterns from patients lying on a bed with a small device and transmits them remotely, such as to nursing stations, is also an indispensable device in hospitals around the world [2-10]. Before the era of packet transmission through AD converter, many of these devices convert the electrocardiogram of a patient from voltage to frequency, and transmit it by frequency-modulated (FM) waves to obtain a sufficient signal-to-noise (S/N) ratio. Specifically, the electrocardiogram signal is modulated as a voice-band FM signal, and the voice-band signal is transmitted by 450-MHz-band FM waves. This is because the S/N ratio required by the F/V conversion element on the receiving side is high.
Unlike the 12-lead electrocardiogram, the amount of information required by the patient monitoring device is not required to depict subtle ST-segment changes, so the amount of information is such that events are included with an analog-to-digital (A/D) converter that acquires 250 samples per second. Considering Nyquist’s theorem, information that can be stored in a 500-Hz band is transmitted in an occupied band of 8 kHz to 450 MHz, meaning that some of the frequency resource is wasted.
In our hawkmoth transmitter, we convert the analog potential of the electromyogram (EMG) into frequency, so the receiving side is required to have a function to obtain a potential proportional to the frequency change. Therefore, this paper describes two methods that do not use FM double modulation. Specifically, the transmitting side performs one V/F conversion, and the receiving side receives the signal as a single side-band (SSB) signal with white noise instead of receiving it in FM. We are considering a method of using digital signal processing (DSP) technology to obtain the frequency from the received signal, and assign a suitable voltage from a lookup table for frequency/potential conversion. Frequency detection and vacant channel detection using the autocorrelation function are also being studied in the field of communications [11-12]. Based on these reports, here we convert the received telemetry signal into a baseband denoised signal with an autocorrelator.
The V/F function of digital processing, which is remarkably effective in denoising and can discriminate even if the frequency is variable, can be used in the future to receive analog signals from micro devices that do not have CPUs nor packet transmitters. For example, if a transmitter with a V/F function with the size of a grain of rice can be inserted directly into the myocardium via a thoracic endoscope and the heartbeat vibration can generate electricity, it will continue to transmit weak noise-level radio waves. If it were attached at the myocardium near the pulmonary venous and send voltage data of the cell, it can be used to predict the atrial fibrillation and to develop drugs that prevent its onset. Applications for in vivo microtechnology are limitless.
In view of such a future, we report the comparison verification of an analog F/V conversion device and digital conversion simulated by MATLAB. We also discuss the reduction of the computation and future prospects related to autocorrelation with polyphase methods.
II. PRINCEPLE
Here, we adopted a method of demodulating the signal using the autocorrelation function, detecting the frequency from the zero-crossing, and giving the corresponding voltage as a digital conversion of the F/V. In this section, we mathematically explain the basis, the norm, the Fourier spectrum by fast Fourier transform (FFT), the power spectrum density function (commonly known as the power spectrum), and the angular velocity ω stored in the autocorrelation of the sine wave.
For each vector in the complex vector space, we define the norm by the inner product (|| ||) (equation (1)). At this time, three properties (equations (2)–equations (4)) hold.
Mathematical definition of period can be defined as follows. If f(t) is assumed to be the magnitude at time t, for a continuous and periodic signal, at a later time nT, f(t)=f(t + nT).
In reality, the received signal is not completely equal, but generally has such a property, and this function is called a periodic function of period T. For the sine function, the period is T=1/(2πf). In this paper, for the purpose of discriminating the frequency of the sine curve using DSP (e.g., FFT and inverse FFT, or IFFT), this period T is such that f(t) = f(t + nT).
The purpose is to obtain the frequency of the sine curve using the autocorrelation function.
In general statistics, in a correlogram, which is a trendgram of the autocorrelation coefficient R, one datum shifted by time Δt is called a lag. Therefore, it is called a sample instead of a lag, and the address AAA is used to express the X-axis address of the correlogram. A single sine curve containing white noise and a signal are output from an A/D conversion device with a sampling rate of XX (Hertz or Sampling Per Second). This signal is taken in a certain window and mathematically processed. In this paper, this window is called a “segment” to distinguish it from the frame size used in FFT. The FFT frame size is 2n times larger, but the segment can be freely resized to improve frequency discrimination.
The spacing of the samples before processing is kept constant, but the time between samples in the segment after autocorrelation processing is not evenly spaced, and the orthogonality of the Y- and X-axes of the correlogram is not preserved. In other words, the multiple samples are arranged in chronological order within the segment, but the relationship between the Y-axis and the X-axis of the correlogram is distorted. Under certain conditions (e.g., when the segment size is an integer multiple of half the wavelength of the frequency of the input signal), the intervals between samples are equal. Conversely, it is possible to focus on this sample sequence with large temporal distortion and use it for frequency discrimination.
The segments are of variable length. Specifically, if the A/D conversion sampling rate is 1 MHz, 1,000,000 samples are output per second. If one segment consists of 4,000 samples, we can divide the data into 250 segments per second, so we can detect 250 frequencies per second.
The autocorrelation function Rff after time τ in the function f is defined as in equation (5). At this time, the inner product of the function (equation (6)) and the norm can be written as equations (7) and equations (8).
The correlation coefficient R (from -1 to +1) between the functions f(t) and f(t+τ) is calculated. In the specific arithmetic processing, whether to divide by the lag or subtract the mean value of the function depends on the result after the experimental arithmetic processing. In other words, is periodicity required from the results? “What is the cycle?” Is it possible to further remove aperiodic noise? “What is the S/N ratio?” These are the evaluations of the calculation process. Basically, periodicity has a high degree of approximation, and noise removal (non-periodicity) has a greater effect.
When used for predicting sunspots, for example, it is better to obtain the lag of each point of the linear function of f(t), but this is not suitable for high-speed processing of the sine function. We recommend the following power spectrum method using FFT and IFFT.
Because the received signal is based on a sine function and its continuity and periodicity are self-evident, we attempted to apply an autocorrelation function using the power spectrum, and developed mathematical logic accordingly. In this section, the received signal is described as g(t) to distinguish it from the above method.
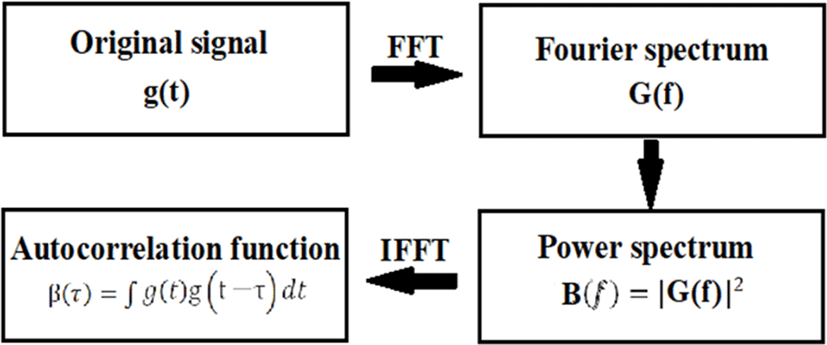
The Fourier transform is defined (equation (9)) as the Fourier integral g(f). Furthermore, its inverse transform g(x) is represented by equation (10). The signal g(x) is often a real number, but g(f) is generally a complex number, and the square of its absolute value is called a power spectrum. This power spectrum is expressed as in equation (11), where * represents a complex conjugate. This IFFT is equation (12), which is obtained from equation (8) and equation (10).
The power spectrum of the signal g(t) is obtained as the square of the absolute value of the FFT. Furthermore, because the IFFT is the norm of equations (10) and (12) with respect to the function at time τ, equation (13) is obtained by applying IFFT to the power spectrum of the FFT. This will yield the self-correlation R on the time axis. The concept of the relationship between power spectrum and autocorrelation function is shown in Fig. 1.
As an advantage, FFT peak detection may erroneously detect double or triple frequencies, but the peak of the autocorrelation function can stably determine the fundamental frequency. The reason is that the frame size of the Fourier transform does not appear in the formula for calculating the peak of the autocorrelation function.
Because the autocorrelation Rff (τ) of the sine wave is the product of the sine wave separated by time τ, it is expressed as equation (14), which is transformed to obtain equations (15), (16), and (17). Because the ratio of integration against τ=0 is the correlation coefficient R, finally equation (19) is obtained. equation (19) means that the autocorrelation function of a sine wave is expressed as the cosine of an even function, and more importantly, the equivalency of its angular velocity ω to the frequency is preserved. In this paper, we use this characteristic to estimate the frequency (only single sinusoidal waves) received by telemetry from the autocorrelation coefficient R.
As shown in equation (13), the autocorrelation is the product of the IFFT function of the power spectrum and the product of time zero and the function separated by time τ. This is repeated m times from time zero (maximum value of τmax), and trial waveforms are drawn. The size of the frame containing the sample is called the segment size (or segment length). If the segments are integer multiples of half-wavelengths of the original frequency, the angular velocity ω is preserved in the correlogram. To obtain the power spectrum, the current signal is sampled at multiples of 22, and this size is called the frame size. Fig. 2 shows the relationship between the original signal and the autocorrelation function, and the concept of the FFT frame size and autocorrelation segment size. The segment size can be chosen to optimize the frequency discrimination according to the frequency of interest.
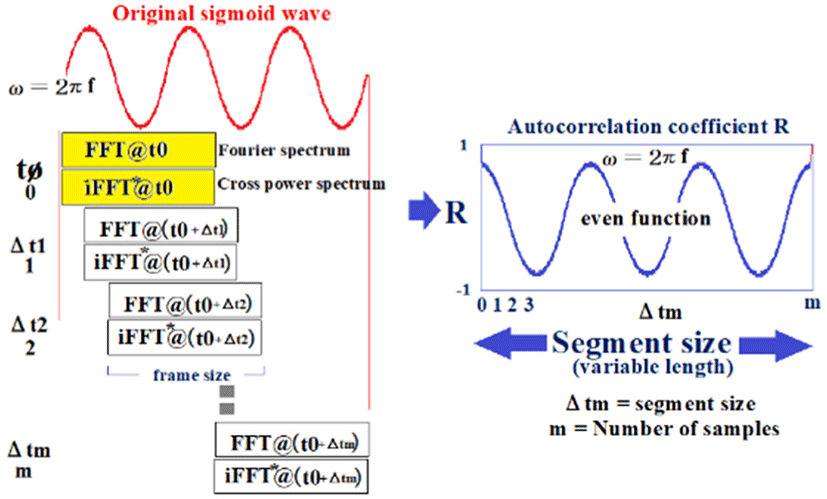
III. METHODS
The biological telemetry assumed here converts a biological signal (potential of, e.g., an electrocardiogram or EMG) into potential and frequency (modulation) and transmits it as radio waves. Then, the receiving side receives the signal secured by the receiving antenna as a SSB. It is demodulated as a baseband (voice band) by the machine.
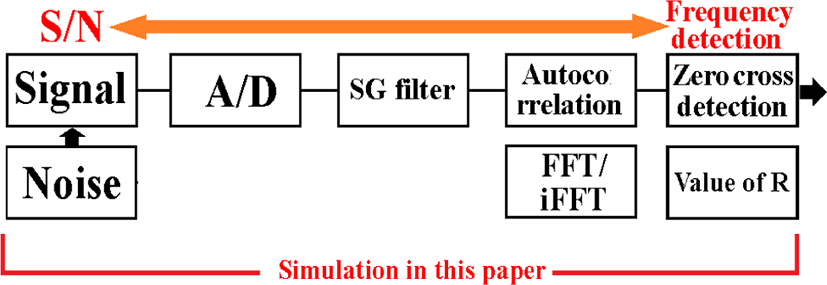
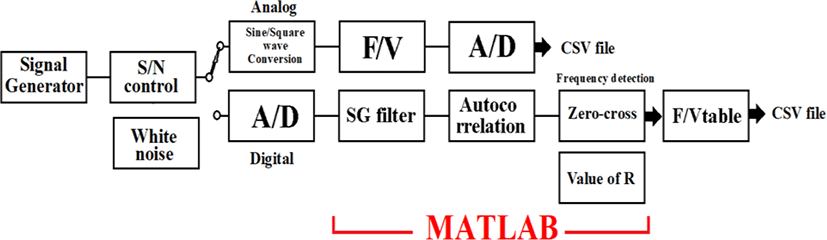
The demodulated signal is a sine wave with white noise and the objective is to find its frequency. This is because the potential of the biological signal can be obtained from the frequency. The function of the block diagram shown in Fig. 3 is described in MATLAB (February 2018 version) as a simulation of frequency detection using the autocorrelation function. Because the S/N ratio is used as a parameter, variable white noise is added, and the sine curve signal is passed through a Savitzky-Golay (SG) filter [13-14], after some degree of denoising, and then the autocorrelation coefficient R is calculated as a cosine function within the segment using correlograms. For frequency discrimination, the zero-crossings on the correlogram are detected, the amplitude of R (value of R) at the center of the segment is obtained, and the correlation between the first zero-crossing address and ¼λ of the actual frequency within the segment is obtained. A block diagram of the functions used in the simulation is shown in Fig. 3, and a summary of the MATLAB functions used is shown in Table 1.
In this article, the purpose is to reproduce FM telemetry signals, and the original signal received by the SSB receiver must meet the following conditions for this simulation to hold:
-
Only one sine wave with white noise is processed.
-
There are no other periodic interfering waves, and of course any noise has no periodicity.
-
The frequency change of the signal is continuous, and the frequency difference from the previous segment is small (frequency fluctuation is less than a few percent).
-
The amplitude of the signal is nearly constant within the segment.
For noise removal, a SG filter is used to prevent deviation of the time axis from the peak values. Finite impulse response is also acceptable, but when measuring multiple channels at the same time, for example, when measuring EMG1 and EMG2, if the finite impulse response coefficients are different, the peak timing will have an error. The noise elimination function is also important, but we want to minimize time axis deviations and phase differences in this system because a phase difference can lead to a potential difference in F/V conversion.
The basic program operation is to take m samples in a segment and apply the autocorrelation function. Because the signal contains white noise (left side of Fig. 4), the power spectrum at this time is the center of the correlogram. The maximum value of R is the first or last ¼λ cosine wave extremum (estimated by an approximation formula).
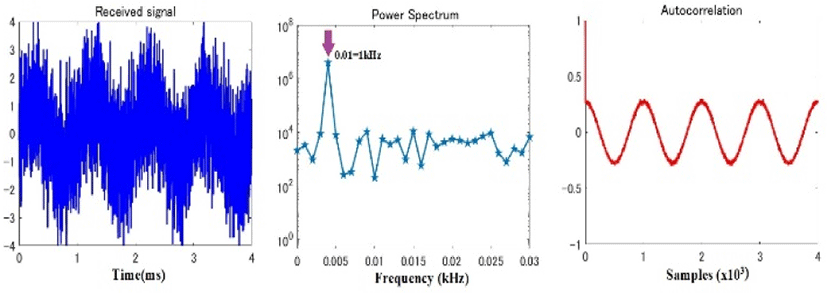
The X-axis of the power spectrum is frequency, and when the noise level is low and a peak value can be obtained, it roughly indicates the frequency of the original signal. However, because the X-axis is logarithmic (multiple of 22), the frequency discrimination ability is poor at low frequencies (center of Fig. 4). However, when an autocorrelator is used, the segment size can be selected according to the target frequency, which allows us to select the length that increases the frequency discrimination ability. In addition, because autocorrelation provides a high denoising effect (right side of Fig. 4), the frequency resolution is dramatically improved compared to that of power spectrum peak detection.
One wave of a signal input at 500–1,500 Hz (intervals of 50 Hz) can be drawn as shown in Fig. 5 by taking the autocorrelation with 4,000 samples/segment at a sampling rate of 1 MHz. For all input vibrations, the maximum value of R is the first or last ¼λ cosine wave extremum (estimated by an approximation). Even if the S/N ratio deteriorates, the waveform is similar and becomes smaller, but the maximum value of R is the maximum immediately after the correlation is started or immediately before it ends. All waveforms are even functions and are symmetrical at the center address, which is 2,000.
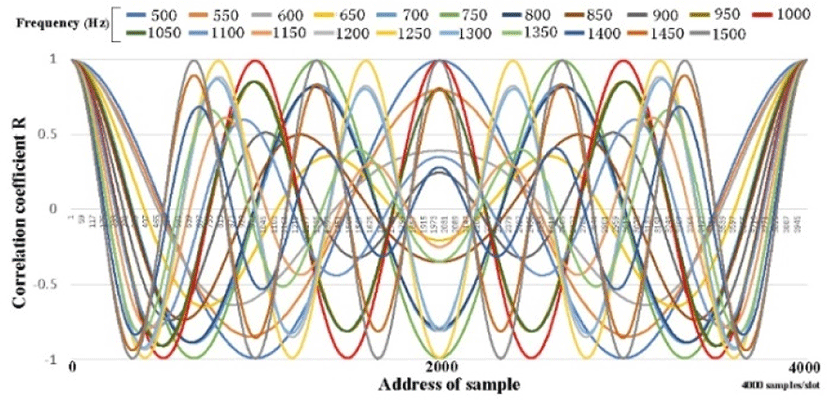
Because it is an even function, we should pay attention to the value of the center address, 2000. At each frequency, as shown in Fig. 6, the magnitude of R is different, but the S/N ratio deteriorates, and the R wave has a small amplitude overall. Even if it becomes a wave, the maximum value R can be grasped by the method described above, and it can be normalized as 1 (Fig. 6). Furthermore, the value of R at the center address of 1,900–2,100 Hz can be drawn in detail as shown in Fig. 7, and of 950–,1050 Hz as shown in Fig. 8. The amplitude of R at the center address is determined by the relationship between the frequency and the segment. If the segment size is an integer multiple of the input half-wavelength, R is 1 even at the center address, and the other frequencies are as shown in Figs. 6, Figs. 7, and Figs. 8. Because the amplitude of the value of the center address R depends on the frequency, this point is an effective factor to increase the frequency discrimination.
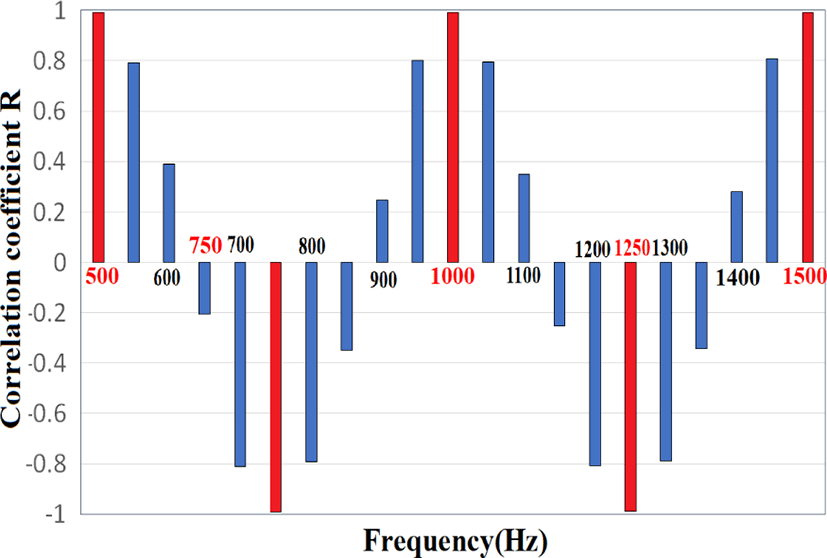
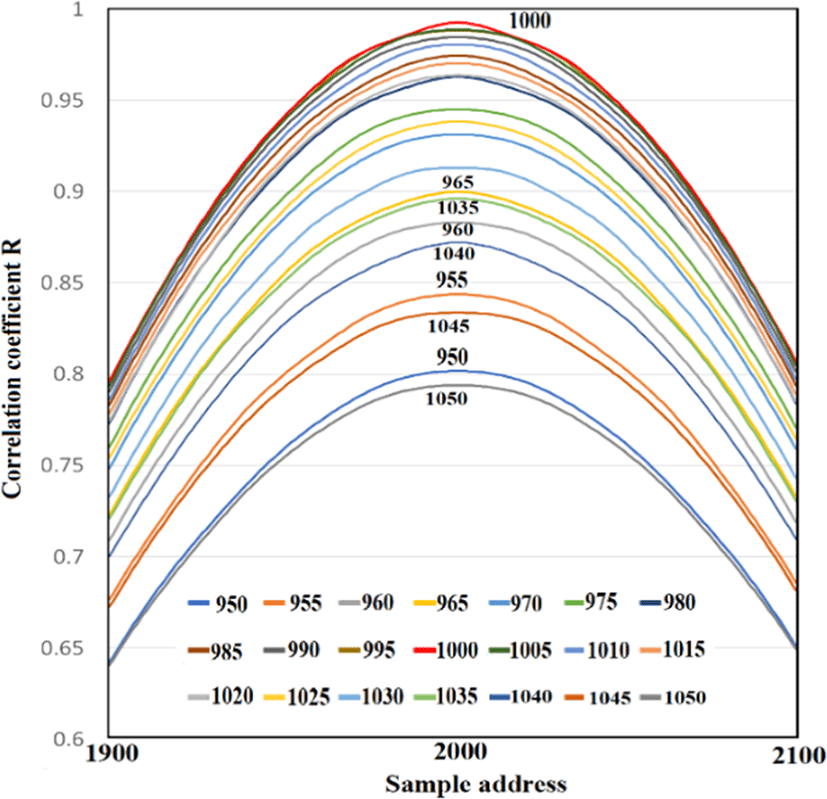
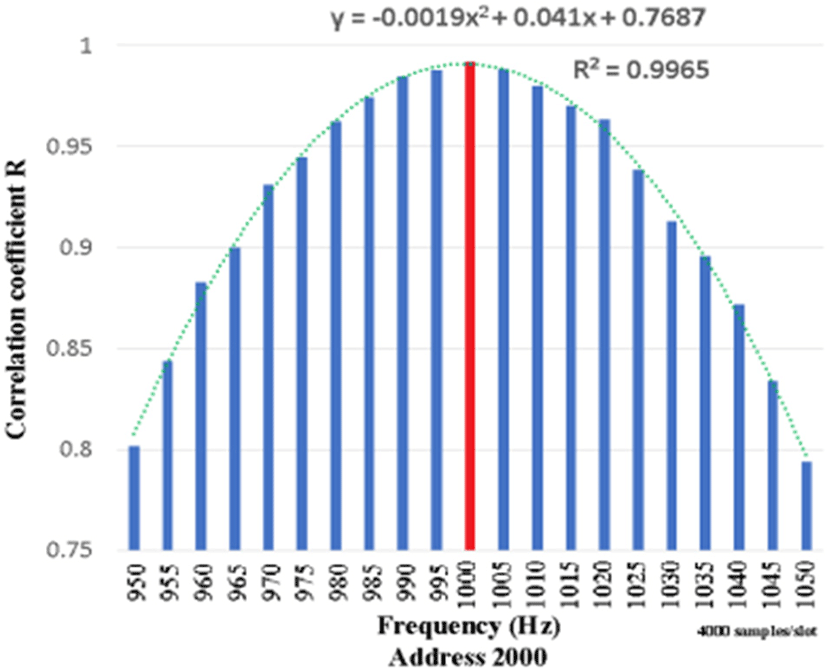
The frequency can be estimated by the approximation formula of the quadratic function.
Fig. 9 shows the correlation between the first zero-crossing of the correlogram and each frequency. If the segment size is an integer multiple of the input half-wavelength, the zero-crossing obtained in the simulation will coincide with the logical value of ¼λ of the input frequency. Similarly, the amplitude of each wave takes the maximum value of R, and the orthogonal relationship between the Y-axis and the X-axis is established, but the coordinates are distorted at other frequencies.
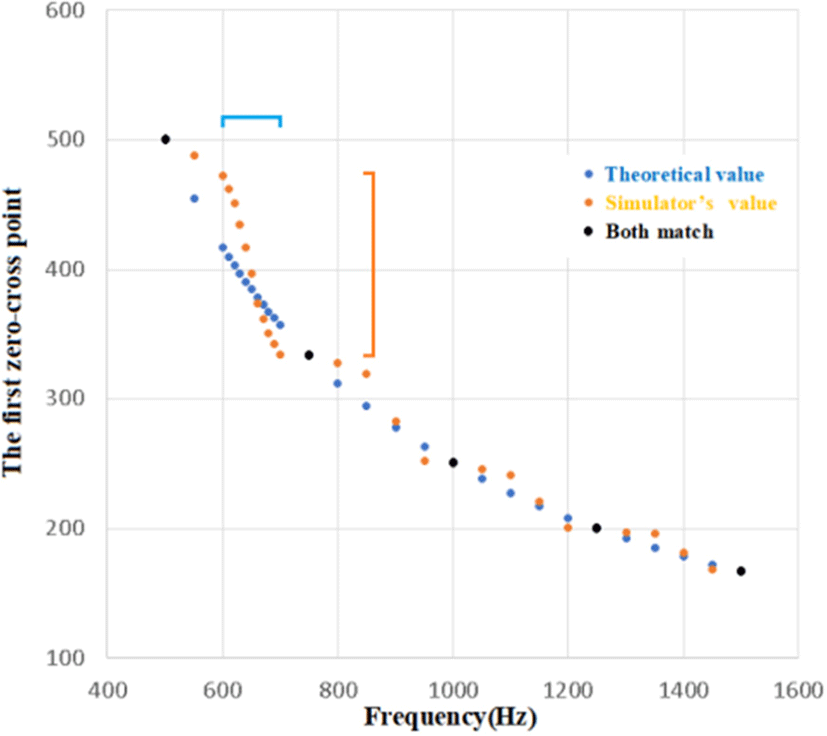
As the input frequency increases, more waves are included in the segment, and the difference between the first zero-crossing obtained in the simulation and the logical value gradually decreases. However, one frequency can be obtained from one segment, so a long segment size decreases the temporal resolution of the biological signal. What is important here is to use a portion with a large dynamic range for frequency discrimination even if the coordinates are distorted. Specifically, the zero-crossing value changes greatly, but, conversely, if the difference between the input frequencies is small, the frequency discrimination ability increases.
As shown in Fig. 9, the first zero-crossing changes greatly for input frequencies of 600–700 Hz, so this portion is used for frequency discrimination. Fortunately, the segment size can be serially passed backwards as information, so the previous frequency is available for backward processing. By varying the segment size based on this information, for example, the segment size can be adjusted to target frequencies corresponding to a segment size of 4,000, or 600–700 Hz (median 650 Hz). In other words, if the previous frequency is 1,300 Hz, the segment size is 2,000, and if the previous value is 1,500 Hz, the segment size is 1733. This can improve the frequency resolution. However, because the part corresponding to 600–700 Hz is not an integer multiple of a half-wavelength, in the above procedure, R will not be 1, but the part corresponding to 600–700 Hz will be affected if the S/N ratio deteriorates. The frequency discrimination is higher than the value of R at the center address.
The sample corresponding to the lag of the correlogram is the value of the multiple integral obtained by performing FFT and IFFT, and the X axis has similar values to the right and left via center line, but mathematically they are independent.
In general, even if there are no adjacent values, the R value can be obtained by calculating against FFT*iFFT of the coordinate zero as one coordinate on the correlogram. However, MATLAB functions do not process if the intervals between the matrix are not uniform, so here we will explain under the condition that the intervals between the segments of 0–2,000 are uniform.
We are interested in the zero crossing of 1/4λ, the amplitude of the central cosine wave (R value), and the amplitude of the cosine wave near the end (R value). It is assumed here that the 2,000-sample waveform of the segment already has a table of correlograms at various S/N levels on the CPU side as a reference. In other words, reducing the number of calculations means, "How far can we reduce the number of samples from 2,000 samples?" Is it possible to maintain the frequency discrimination ability and withstand actual use? is. If the computational processing is lowered, the discrimination ability will be lowered, so it is a conflict with the needs.
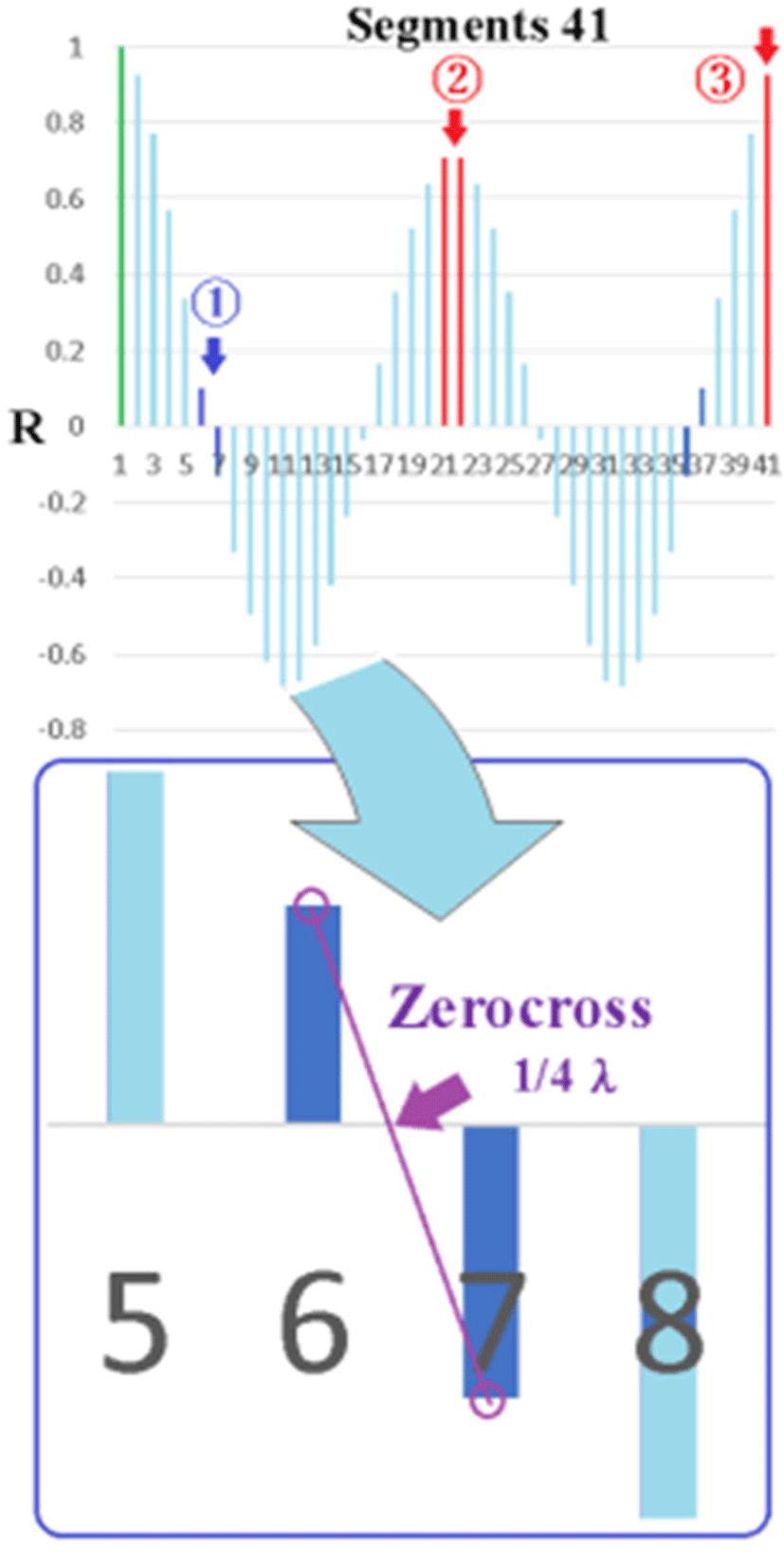
In order to visually understand this theme, Fig. 10 shows the correlogram when it is temporarily reduced from 2,000 samples to 40 samples (41 calculations because there are actually zeros shown in green allow).
The points to watch are arrows 1, 2, and 3. The first 1 is the 1/4λ zero crossing, and the coordinates of the zero crossing are obtained using the auxiliary line. Arrow 2 is the median value of the sample, and there are two values, but since it is an even function, they are almost the same value. The third arrow obtains the R value near the end in order to obtain the reference value of the R value with S/N. From this 1, 1/4λ is obtained, and from 2 and 3, two candidate λs are obtained (one value is close to 1/4λ, the rest are imaginary). As a result, the number of calculations for FFT and IFFT is reduced to 2001 or 41, and the calculation reduction rate is 98% reduction, and the remaining 2% should be calculated. Furthermore, if it is 41 segments, Savitzky-Golay (third order, 17 points) can be used, and there is also a denoising effect.
In this way, the autocorrelation coefficient R for a sine curve can always be drawn as a cosine and becomes an even function that folds back at the median. With this in mind, as mentioned above, it is also possible to cut 41, 98% reduction of the FFT calculation from 2001, lighten the CPU and DSP calculations, and pave the way for implementation.
We generated a stable 1,000-Hz signal from a signal generator, added white noise, changed the S/N ratio, added noise to the analog element, recorded the resulting voltage with a sampling speed of 500 kHz, processed the potential with a 16-bit A/D conversion, and recorded the result in a CSV file. On the digital side, A/D conversion was performed under the same conditions, the data were imported into MATLAB on a PC, and the frequency component of the autocorrelation coefficient R was obtained and recorded in a file. Then, these two files were compared. A block diagram of the evaluation experiment is shown in Fig. 11, and Fig. 12 shows the F/V converter circuit diagram and board used in the analog circuit.
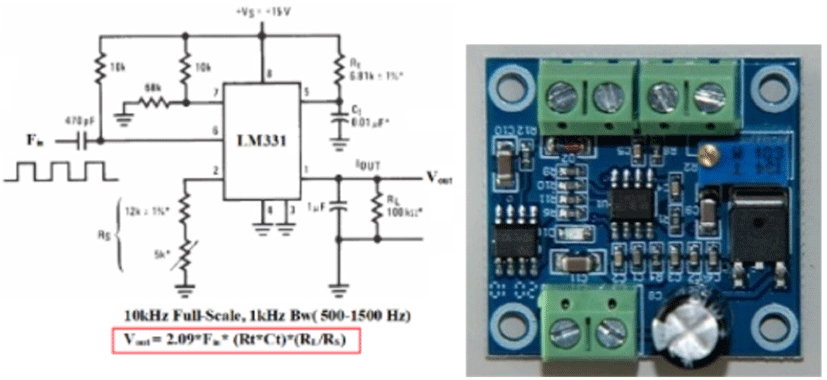
A comparison of the two measurements is shown in Table 2. The F/V conversion element calculated the frequency from the potential fluctuation. The length of the 1,000-Hz signal was 400 ms, 400 segments were measured, and the standard deviation was obtained. The S/N ratio of 8 dB in the F/V conversion circuit is almost equal to the autocorrelation function of –14 dB, with a standard deviation of ±4, and the difference is 22 dB. A standard deviation of ±4 Hz is the limit for practical use.
| Input frequency 1,000 Hz | S/N (dB) | Standard deviation of error (Hz) |
|---|---|---|
| F/V analog device | +20 | +/−0.2 |
| +8 | +/−4.1 | |
| Autocorrelation+SG | +8 | +/−0 |
| −11 | +/−1.8 | |
| −14 | +/−4.0 |
Using a chicken electrocardiogram, we compared the signal before V/F conversion, the demodulation by the analog F/V element, and output from the digital processing autocorrelator (250 segments/second) (Fig. 13). As for the V/F frequency characteristics on the transmitting side, the dynamic range peaks at high frequencies, so the R-wave head is suppressed. Even so, the autocorrelation function does not clearly show high amplitude in the R wave, but this is because a SG filter is applied to improve the S/N ratio. Unlike FIR, the SG filter does not generate a temporal delay in the amplitude, but the amplitude drops to some extent. Similarly, the amplitude of the R wave is also falling in the F/V element, but this is because it is a low pass filter due to the effect of the time constant added in parallel to the output.
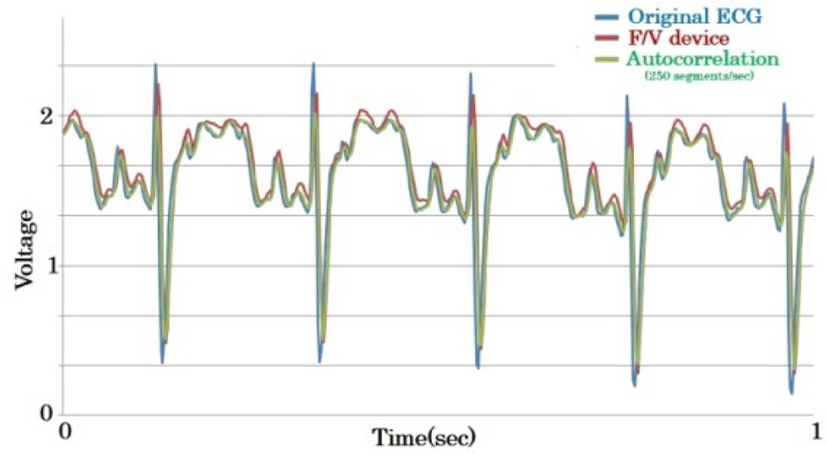
Even if the above exclusions are taken into account, it is clear that the R wave is still significantly pumped in autocorrelation and cannot follow a frequency that rises instantaneously. This shows the limitation of analyzing only one segment, and to solve this, we should incorporate forward prediction by deep learning based on past data, and implement a parallel computing method by polyphase and multiple-segment operation.
IV. CONSIDERATIONS
In this study, the band of the transmission frequency was relatively narrow at 1 kHz, so the SSB baseband frequency was 500–1,500 Hz. Theoretically, only 500 pieces of information per second can be carried in a 1-kHz band according to Nyquist’s theorem, so a frequency resolution of 2 Hz is sufficient. In addition, the fluctuation of the autocorrelation function, based on its standard deviation, is ±2 Hz, so the resolution is 4 Hz, or 250 segments/second. [Please verify that the editing is consistent with your intended meaning.] To increase the resolution of the potential axis in the future, it is necessary to improve the following conditions:
-
Increase the frequency band on the transmitting side. For example, if 0.01V is 4 Hz, and this is changed to 40 Hz, the error of 4 Hz becomes 0.001 V.
-
Widen the baseband frequency band of the SSB receiver. For example, if the band is increased from 500–1,500 Hz to 2,500–3,500 Hz, the frequency resolution will triple. In this case, a software DSP receiver (software-defined radio receiver) is more suitable than an SSB receiver, whose reception band is fixed by a crystal filter.
-
Increase the number of A/D converters working in parallel. By increasing the number of A/D conversion elements and attaching an autocorrelation function to process them, the frequency resolution will increase.
Rather than converting the input signal from analog to digital and passing this data string to the DSP field-programmable gate array (FPGA) after time-sharing, multiple A/D converters are arranged in parallel and operated with a time difference, and the autocorrelation function is used in each calculator to find the R values at zero-crossings and segment centers to speed up the process. If the segment can be varied by passing information on the frequency of the preceding segment to the subsequent calculation unit, high frequency discrimination ability can be obtained.
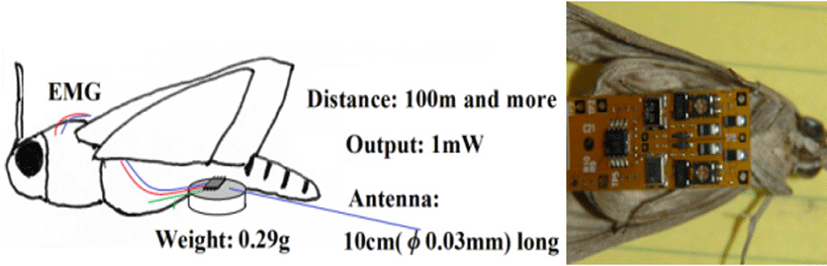
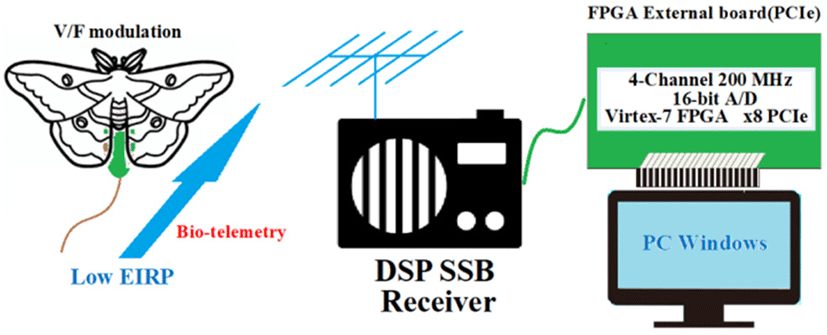
For research subjects that cannot carry a CPU, such as moths, butterflies, and sparrow-sized birds, the payload is limited, the battery is limited, the transmission power is small, and the antenna is small, resulting in an extremely small effective isotropic radiated power (EIRP) [Please verify that I defined EIRP correctly.] (Fig. 14). Therefore, it is not easy for the receiving side to obtain a sufficient S/N ratio. In conventional biotelemetry transmission, both primary and secondary modulations are frequency conversions, occupying a wide frequency band and not effectively using frequency resources. Note that the existing method uses a large transmission power.
For small subjects, such as moths, butterflies, and small birds, our proposed digital processing (autocorrelation function) enables efficient use of frequencies and reproduction even when the S/N ratio is low [15-18].
Polyphase segment processing is a method of detecting frequencies by running multiple segments at the same time. A handling protocol is required to distribute data from the A/D converter to multiple computing units. In this way, the processing time can be shortened.
What elements are needed to implement the above algorithm? The specific proposal here is the FPGA + A/D board, Model 78760 (PC expansion board for Windows). This board is a PCI Express board with 200-MHz 16-bit 4-channel ADC and a Virtex-7 FPGA. As mentioned above, the autocorrelation functions are only general-purpose FFTs and IFFTs, so the design is easy, and processing three autocorrelation functions in parallel does not pose a problem in terms of capacity. Because 4-GB DDR3 SDRAM is mounted on this board as an external memory for the FPGA, it is also possible to store data temporarily. The host interface is a PCIe x8 lane, through which data can be transferred to Windows at high speed (Fig. 15). By inserting a board with an FPGA capable of four self-functions and a 4-channel A/D converter into the expansion bus of the PC, the frequency discrimination ability will improve fourfold in the time axis direction.
Autocorrelation functions using power spectrum require high-speed calculations, so there have been reports of FFT, iFFT and related processing being implemented in FPGA. The reported implementations are extremely helpful for this research [19-22].
V. CONCLUSION
A MATLAB program was developed to calculate the half-wavelength of a sine-curve baseband signal with noise by using an autocorrelation function, a SG filter, and zero-crossing detection. The frequency of the input signal can be estimated from 1) the first zero-crossing (corresponding to ¼λ) and 2) the R value at the center of the segment. Thereby, the frequency information of the preceding segment can be obtained. If the segment size were optimized, and a portion with a large zero-crossing dynamic range were obtained, the frequency discrimination ability would improve.
Using an FPGA board with multiple A/D converters and multiple high-speed computing units makes it possible to quickly transfer the information of the previous segment backwards, allowing the algorithm to be implemented in Windows.