I. INTRODUCTION
Today online world is our new home, many of our activities, in fact most of our activities like many students are going online classes, many of us actually book tickets online, most of our people actually also doing online shopping, and the communities are also conducting online conferences. In recent decades, networks have expanded from being a simple means of communication to being an integral part of nearly every aspect of our modern lives. The scale, speed, and dynamic complexity of networks have all increased. Cyberspace is what the Internet has become due to the widespread usage of computers and networking technology. Cyberspace, or the virtual environment enabled by computers and networks, is an environment where people all over the world may talk to each other using the Internet and other electronic means [1-2]. As a new frontier of people, cyberspace has reached a broad consensus. How to better explore and represent cyberspace has attracted wide attention around the world. Since 2012, the United States had launched the “Treasure Map Project” and the “mission X” to study real-time and interactive global Internet maps, which provided basic support for research on cyberspace information [3]. In 2014, Kaspersky lab in Russia released its new interactive cyber threats real-time map, which was dedicated to real-time representation of network activities [4]. In 2018, China Internet Security Conference (CISC) showed the smart city system, which integrated basic cyber information and showed it in a centralized way, so as to monitor and respond to cyber security attacks in real time [5].
Given the heterogeneous network paradigm [6] and different applications such as terrestrial communication network [7], mobile marine network [8], aerostat platform [9] and satellite communication networks [10], the form of cyberspace is often complex and heterogeneous, so the research of this paper is based on complex-heterogeneous cyberspace [11].
Visualization is a graphical representation that uses appropriate graphs, charts and maps to represent the relationships between data [12-13]. As a technical method of spatial cognition and representation, cartographic visualization is not only limited to the surface space, but also can be extended to the space beyond the surface [14-15]. Visualization research is very important, and ground-based Internet cartographic visualization is even more important. While geographical data is related to spatial location and closely related to visualization. Cyberspace cartographic visualization can be applied to typical business scenarios such as real-time monitoring of cyberattacks, traceback of cyber security events, communication support, and so on. So it is obviously significant for the research on complex-heterogeneous cyberspace cartographic visualization.
In traditional geographical space, map as an important carrier of describing geographical phenomenon, which has been an indispensable tool for operational command since ancient times [16]. The traditional method of data visualization analysis is to draw corresponding graphs to make people better understand the data. Currently, it is needed for cyberspace map that can fully show the information of cyberspace, so as to establish the connection between cyberspace and geographical space. The ultimate goal of the cyberspace visualization is to fully show cyber information in the form of cyberspace map and realize the visualization and digitization of cyberspace, and thus provide intuitive and valuable information for decision-makers to reduce the uncertainty of decision-making. The early stage of the development of cyberspace visualization is faced with problems such as weak theoretical basis and immature technology, while the introduction of big data and artificial intelligence (AI) provides a new perspective for the research of cyberspace visualization [17].
Although computer vision and multimedia systems are not directly related to cartographic visualization, there are some applications of computer vision techniques that can be useful for processing and analyzing visual data in cartographic visualizations. For example, computer vision techniques such as object detection and tracking can automatically identify and label features on a map, such as roads, buildings, and bodies of water. Image segmentation techniques can be used to separate different regions or layers of a map, such as land and water or different types of land use. Machine learning techniques can also be applied to classify and predict patterns in geographic data. For example, clustering algorithms can group similar features on a map, such as neighborhoods or land use types. Classification algorithms can predict the likelihood of certain features or events occurring in a particular location, such as the likelihood of flooding in a particular area. Additionally, multimedia systems can play a role in creating interactive and immersive cartographic visualizations that allow users to explore and interact with geographic data in new ways. For example, virtual reality and augmented reality technologies can create immersive experiences allowing users to explore geographic data in three dimensions. While cartographic visualization may not be directly related to computer vision or multimedia systems, some applications of these techniques can be helpful in processing and analyzing visual data in cartographic visualizations and creating interactive and immersive experiences for users.
Deep learning is a form of machine learning that takes its cues from the structure of the human brain; in the context of deep learning, this structure is known as an artificial neural network [18]. Deep learning has the advantages such as well learning ability and data-driven with high threshold. While along with various advantages of neural networks, the most common ones are classification and cluster. The strong combination of deep learning and neural networks is deep neural network (DNN), which happens to be close to the problem of cyberspace visualization.
LLE is a dimensionality reduction technique that focuses on capturing the local structure of the data. It seeks a lower-dimensional data representation to preserve the pairwise distances between neighboring points. The preservation of local relationships allows for a meaningful visualization of the data while reducing the dimensionality. LLE can be particularly valuable in complex and heterogeneous cyber data. Cyber data often consists of high-dimensional and diverse attributes, such as network connections, protocols, time-stamps, and other relevant features. Applying LLE can effectively reduce the dimensionality of this data while retaining its essential characteristics, enabling a more concise and meaningful representation that captures the underlying structure and relationships of the data. First, it helps overcome the curse of dimensionality by reducing the dimensionality of the data, which can be beneficial for visualization purposes. Second, LLE preserves the local structure of the data, allowing for a more accurate representation of the data’s inherent relationships. It is imperative in complex and heterogeneous cyber data, where understanding the local interactions and dependencies is crucial. Integrating vector autoregressive moving average (ARMA) for spatiotemporal data modeling is another unique aspect of their approach. ARMA models are widely used for time series analysis, and by applying it to the spatiotemporal aspects of the data, it demonstrates their ability to capture and analyze temporal patterns and dependencies within the network. This integration enables a comprehensive understanding of how the network evolves, adding an essential temporal component to their visualization technique. Furthermore, the use of DNN for training is noteworthy. DNN has demonstrated exceptional capabilities in learning complex representations and patterns from data. By employing a DNN in the complex heterogeneous cyber cartographic visualization, we leverage the power of deep learning to extract meaningful features and representations from the cyber data, enabling a richer and more accurate visualization of the network.
The paper is structured as follows. Section 2 reviews the related work. In Section 3, we study the DNN based complex-heterogeneous cyberspace cartographic visualization. The experimental results are shown in Section 4. Section 5 concludes this paper.
II. RELATED WORK
In today’s digital age, we are continually bombarded with information, most of it may or may not be reliable. Although raw data is used to determine if something is genuine or incorrect, it is rarely presented to the public. It is easy to understand how rows upon rows of numbers may be difficult to interpret. Because of this, we commonly use data visualization to present patterns and trends in data more easily. In [19], the authors presented a novel distributed union-find algorithm that features asynchronous parallelism and k-d tree-based load balancing for scalable visualization and analysis of scientific data. In [20], the authors proposed a new perspective of ensemble data analysis using the attribute variable dimension as the primary analysis dimension. Using matplotlib callbacks, visualization toolkits, and embedded HTML visualizations, the authors of [21] demonstrated three methods for incorporating interactive visualizations into Jupyter Notebooks. In [22], the authors introduced the interactive catchment explorer, a web-based interactive data visualization platform for investigating environmental information and model results. For the purpose of visualizing abstract gaze data, the authors of [23] presented a data processing approach based on gaze behavior. To accurately incorporate information about transcriptomic variability into the visual interpretation of single-cell RNA sequencing data, the authors of [24] presented den-stochastic neighbor embedding and dens manifold approximation and projection, density-preserving visualization tools based on t-stochastic neighbor embedding and uniform manifold approximation and projection, respectively. A novel graphical tool for the visualization of health data was published in [25], which may be used to quickly monitor patients’ health condition remotely. In [26], the authors suggested a new supervised dimension-reduction approach termed supervised t-distributed stochastic neighbor embedding, which achieved dimension reduction while maintaining the similarities between data points in both the feature and outcome spaces. The suggested technique can handle high-dimensional data, making it useful for both prediction and visualization applications. Combining illustration with data visualization was investigated in [27], where the authors presented interactive picture segmentation and gridding techniques. While many studies have focused on visualizing data in a homogeneous network, complicated heterogeneous cyberspace has received far less attention.
The term “cyberspace visualization” refers to the use of visual language to explain and analyze a wide range of cyberspace phenomena and occurrences, such as the visualization of network elements, network structure, and security incidents. Cyberspace information system was described in [28] as a parallel to geographic information systems, with the latter allowing for visualization based on a geographical coordinate system. This led to the proposal of a multi-dimensional and multi-view cyberspace information system model. In [29], the authors created an architecture for visualizing the cyber battleground from border gateway protocol archive data, which included border gateway protocol connection information data from routers all over the world. In [30], the capability demand of the joint operation for cyberspace war scenario visualization system was used to do the system function analysis. In [31], two generalization approaches were presented after analyzing and measuring different forms of characteristic information of point cluster characteristics in cyberspace from four perspectives: statistics, metrics, topology, and themes. In [32], an ontology-based knowledge representation method for cyberspace situational information elements was proposed; this study aided in the understanding, modelling, and presentation of the cyberspace environment, and it served as a useful point of reference for the study of related technologies. In [33], the authors suggested the connotation and technological route of cyberspace visualization based on the idea of the “man-land-network” nexus and explain the visualization of cyberspace elements, cyberspace relations, and cybersecurity incidents. In [34], considering that the distance cartogram could express the characteristics of spatial relational information in a simplified and deformed geographic space, a composite distance cartogram was designed according to the cyberspace information visualization model. To generate a cyberspace composite distance cartogram, the coordinate transformation principle and method for the nodes of network communities were proposed. In [35], from the basic concept of cyberspace, based on the geospatial information grid, the authors studied the network space physical domain, logic domain and social domain partition method respectively. In [36], according to the spatial correlation degree of cyberspace and its elements, mapping methods for cyberspace were classified and the key technologies that needed to be solved were proposed. To the best of our knowledge, there are almost no researches on using DNN to realize cyberspace visualization, even with regard to complex-heterogeneous cyberspace. However, the research on DNN based complex-heterogeneous cyberspace is an essential part in cartographic visualization, which motivates this paper.
III. CYBERSPACE CARTOGRAPHIC VISUALIZATION
In light of the complexity and heterogeneity of cartographic data in complex-heterogeneous cyberspace, it is necessary to reduce the data dimensionality and greatly reduce the workload of DNN. Dimensionality reduction process reduces the number of random variables or features under consideration in a machine learning algorithm. Data dimensionality reduction refers to the process of mapping a sample from a high-dimensional space to a low-dimensional space through linear or nonlinear mapping to obtain a meaningful low-dimensional representation of high-dimensional data.
Data dimensionality reduction methods are commonly divided into linear methods and nonlinear methods, which can be used for data visualization. Although the linear method is simple to calculate, it cannot find the nonlinear regularity of distribution of data, especially for the manifold distribution data. In order to overcome the problem of nonlinear distribution of data in this paper, LLE is introduced to reduce the data dimensionality. LLE unfolds the nonlinear manifold in a piece-wise manner. Each piece is unfolded and the unfolded pieces are put together to have the entire unfolded manifold. The steps of LLE is summarized as follows.
-
(1) Select neighbors and construct k-nearest neighbors (kNN) graph.
-
(2) Reconstruct with linear weights. Find the reconstruction weights for each point based on their neighbors.
-
(3) Map to embedded coordinates. Use the obtained weights to embed the points in the low dimensional subspace.
The T-dimensional training dataset is represented by X = (x1, x2,...,xq) ∈ ℝT×q, while t-dimensional training dataset after dimensionality reduction is represented by Y = (y1, y2,...,yq) ∈ ℝt×q. The distance between xm and xn is denoted as (xm, xn).
A kNN graph is formed using pairwise Euclidean distance between the data points. Therefore, every data point has k neighbors. Let Pm denote the adjacent points set. Then compute the linear reconstruction coefficient ωm for xm.
The linear reconstruction coefficient ωm is kept unchanged, and the lower dimensional space coordinate ym corresponding to xm is solved. The constraint is and , where I is the identity matrix.
The core of LLE algorithm is the establishment of reconstruction coefficient. Let denote the matrix composed of k nearest neighbors of xm, and the matrix composed of kxm is represented by X = (x1, x2,...,xq) ∈ ℝT×q.
where M = (X − Φ)T (X − Φ), and because ∑n∈Pmωmn = 1, xm = Xωm. Therefore, ωm can be calculated as follows.
where E = (1, 1,...,1)T, then Lagrange function is constructed as follows.
where λ is the Lagrange multiplier. Taking the derivative of equation (5) with respect to ωm and λ, and we have
According to equation (6), and we have
The calculation of low dimensional coordinates in equation (2) can be embedded by coefficients construction in equation (7).
Given the above, the reconstruction coefficient ωm of each xm contains local information in high dimensional data, and the characteristics of the related data can be well preserved in low dimensional data. The value of ωm determines whether dimensionality reduction can be completed.
DNN is used to train the cartographic coordinates data obtained after data dimensionality reduction to reduce the workload of DNN.
During DNN training, a certain number of samples are used to form a Mini-batch. Supposing that the dimension of each sample is T and the number of samples is Q, then each Mini-batch is a matrix of T × Q. The whole training process will go through three parts: forward computation, backward computation and weight updating. Assuming that the layer number of neural network is L. In forward computation process, the output layer O after training is obtained through input Mini-batch computation, and the process can be expressed as follows.
where x is the input Mini-batch data, that is, the data of input layer. yγ is the hidden layer result of γth layer. w(γ) and b(γ) are the weight and bias of γth layer network respectively, and z is the output value of forward computation. Additionally, relu( ) and softmax( ) are forward activation functions corresponding to two different operations in forward computation process respectively.
Data of cartographic in complex-heterogeneous cyberspace mainly includes coordinates and other data such as device, application, data, IP, protocol and subject of network. Several data different modeling methods are described in terms of temporal and spatial attributes in order to realize complex-heterogeneous cyberspace cartographic visualization.
There are many time series metrics in multidimensional data. Time series is basically a sequence where we record a metric over regular intervals. For a certain kind of network security event in complex-heterogeneous cyberspace, the risk distribution of such event can be forecasted by these metrics with time attribute. The following models are mainly used, which model to choose in practical application depends on the time fluctuation and dependence of data.
The ARMA model, which combines the AR model and the MA model, is a crucial tool for studying time series. Forecast index data across time is treated as a random sequence by ARMA. This collection of random variables is dependent on one another, which symbolizes the timelessness of the original data. Assuming that the impact factors are u1, u2,…, uk, and the forecast object can be obtained by regression analysis.
where Y is the observed value of the forecast object. Et is the error. As a forecast object, and Yt is affected by its own changes according to the following equation.
Error has dependencies in different phases, which can be defined as follows.
Thus, the expression of ARMA model can be defined as follows.
Auto regressive integrated moving average (ARIMA) model is a forecasting algorithm that takes into account previous past values to forecast future values because it considers that the information is found in those past values can be indicative of future values. The ARIMA model is defined by the three parameters p, d, and q. For a stationary time series, p is the order of the auto regressive term, d is the order of differences, and q is the order of the moving average term. The number of lags in the dependent variable (p), the number of differenced iterations (d), and the number of lags in the error term (q) are all displayed in the ARIMA (p, d, q) model. For instance, the ARIMA model with parameters (1,1,2) contains a one-lag dependent variable (1), a first-difference stationary (1) variable, and a two-lag error term (2). In this case, the ARIMA model comprises a one-lag dependent variable (1), a zero-lag independent variable (0), and a one-lag error term (1). ARIMA (1,0,1) equals ARMA (1,1) if the series is level.
The distinguishing factor between the ARIMA and ARMA models lies in the former’s ability to convert non-stationary time series into stationary time series via differential operation, thereby facilitating modelling. The specific equation of ARIMA is the same as ARMA except that a difference operation is added before modeling.
Autoregressive conditional heteroskedasticity (ARCH) model conveys that the series in question has a time-varying variance (heteroskedasticity) that depends on (conditional on) lagged effects (autocorrelation). ARCH model takes all available information as condition and uses the form of auto regression to describe variance variation. For time series, available information is different at different time, and the corresponding conditional variance is also different. ARCH model can be used to describe the conditional variance with time variation.
The basic idea of ARCH model is that under the previous information set, and the occurrence of a noise at a certain time is Gaussian distribution. The mean of the Gaussian distribution is zero and the variance is a quantity that changes over time (i.e., conditional heteroscedasticity). While the time-varying variance is a linear combination of the squares of the past finite term noise values (i.e., auto regression), which constitutes the ARCH model.
Let the error variance be time-varying, that is, heteroscedastic and call it ht, then the basic ARCH(1) process is defined as follows.
When a big shock occurs in the previous period t − 1, it is more likely that the value of ut in absolute terms will also be bigger, that is, when is small or large, the variance of the next innovation ut will also be small or large. The ARCH(q) model can be defined as follows.
To resolve the problem of negative estimates, the generalized ARCH (GARCH) model is developed, which includes the lagged conditional variance terms as autoregressive terms and uses few parameters to capture long lagged effects.
Based on ARCH(q) model, the GARCH (p, q) model can be defined as follows.
The GARCH (1,1) model contains one lagged term of the conditional variance (h) and one lagged term of the squared error (u2).
Each object, event or phenomenon of complex-heterogeneous cyberspace is associated with time and space, resulting in a wide range of spatiotemporal application fields. Spatiotemporal data model is the basis of spatiotemporal data management, and the effective processing of spatiotemporal data needs to be based on spatiotemporal database model.
The metric with both spatial and temporal attributes in complex-heterogeneous cyberspace is the coordinates of devices or subject of network. In complex-heterogeneous cyberspace cartographic visualization, the risk distribution of network security event can be forecasted in order to realize the “battle on map”. Taking coordinates in multidimensional data as an example, the change of the coordinates of a node with time is a time series analysis problem, but if the coordinates of other nodes change, the coordinates of the node may also change accordingly. Therefore, the analysis of spatial data is also designed. The specific method is defined as follows.
where Φchc is the autoregressive coefficient of complex-heterogeneous cyberspace, Cchc is the coordinate weight matrix, ut−1 is the autoregressive term, bt is the moving regression current deviation, Θchc is the moving regression coefficient, and bt−1 is the moving regression deviation term. The model used in this paper is vector ARMA (VARMA) model with spatial dependence.
IV. SIMULATION RESULTS
The proposed DNN based complex-heterogeneous cyberspace cartographic visualization is implemented via three parts. First, LLE method is introduced to reduce the data dimensionality. Then, DNN is used to train the data after dimensionality reduction. Finally, in order to realize complex-heterogeneous cyberspace cartographic visualization, the data model is designed with respect to temporal and spatial. The computational simulation is being executed on a computing equipped with an Intel i9-11900k processor operating at a frequency of 3.5 GHz, and a memory capacity of 16 GB with a clock speed of 2,666 MHz. The simulation is driven based on cyberspace datasets available on data.world. In the simulation, three algorithms are selected with comparison: a differential privacy enabled DNN learning framework (DNN-DP) [37], channel state information (CSI)-based DNN (CSI-DNN) [38] and convolutional autoencoder with residual blocks-DNN (CAERES-DNN) [39]. The evaluation of simulation results often involves the utilization of three classification metrics, namely precision ratio (P), recall ratio (R), and F1 score (F). These metrics are commonly employed to compare and assess the quality of the aforementioned results. The value of P denotes the level of accuracy in the recognition of coordinates. The value of R represents the extent to which the visualization outcomes encompass the cyberspace. The metric F provides a comprehensive assessment of both precision (P) and recall (R).
The model of DNN based complex-heterogeneous cyberspace in simulation has a total of nine layers, among which the number of nodes in the hidden layer is 2048, the number of nodes in the top layer is 8992, and the number of nodes in the input layer is 400. The network parameters are initialized with Gaussian distribution with mean value of 0 and variance of 1. The size of Mini-batch is set to 200.
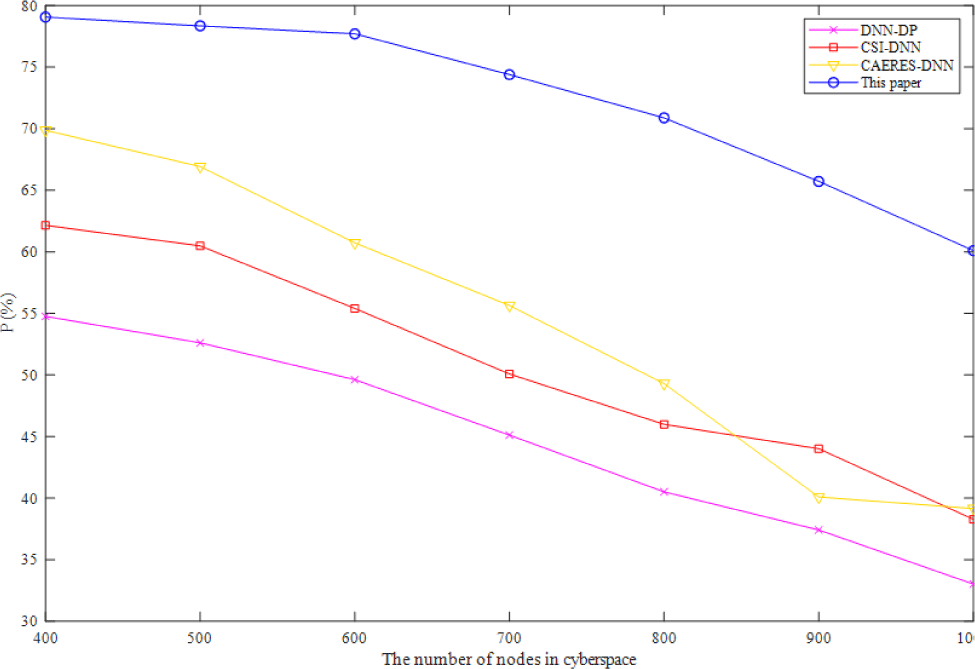
Fig. 1 describes the trends of the precision ratio of the model with four algorithms in complex-heterogeneous cyberspace cartographic visualization. Increasing the number of nodes in cyberspace has a negative effect on the accuracy of all algorithms, as shown in Fig. 1. However, the accuracy of the method suggested in this study remains consistently greater than the accuracy of the other three baselines. Compared with sigmoid activation function, the method proposed in this paper with ReLU activation function has three main changes, which are unilateral inhibition, relatively wide excitatory boundary and sparse activation. The compared three baselines with sigmoid activation function have the fatal error that if the initial number of nodes in cyberspace is large, most neurons may be in the saturation state and kill gradient, which will make the network difficult to learn. As a result, the precision ratio of the method suggested in this study is greater than that of the other three baselines, and its theoretical accuracy is higher as well.
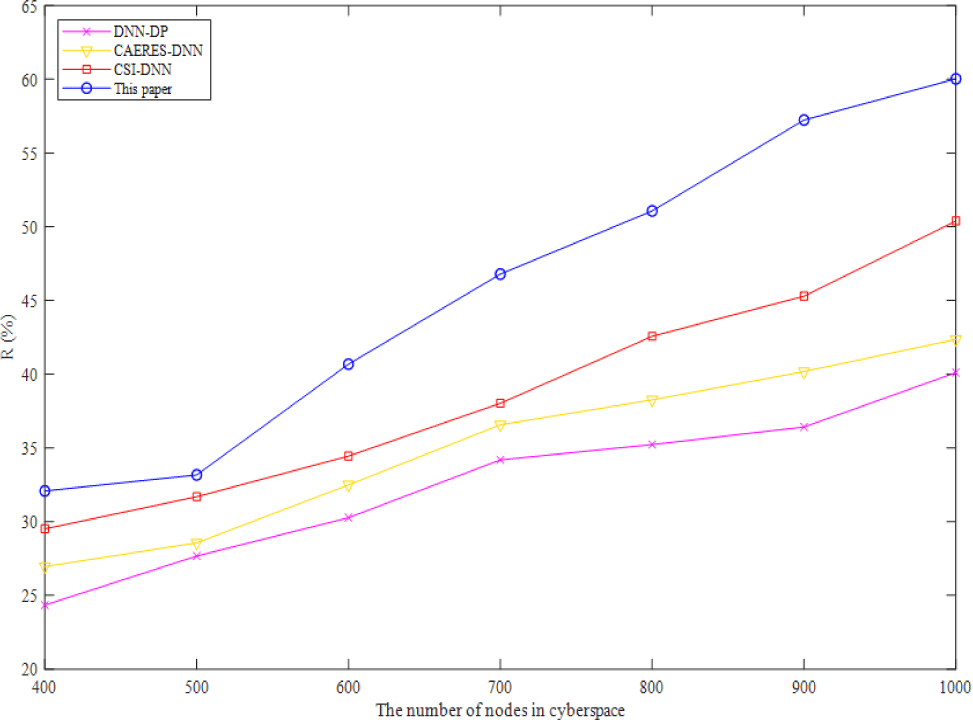
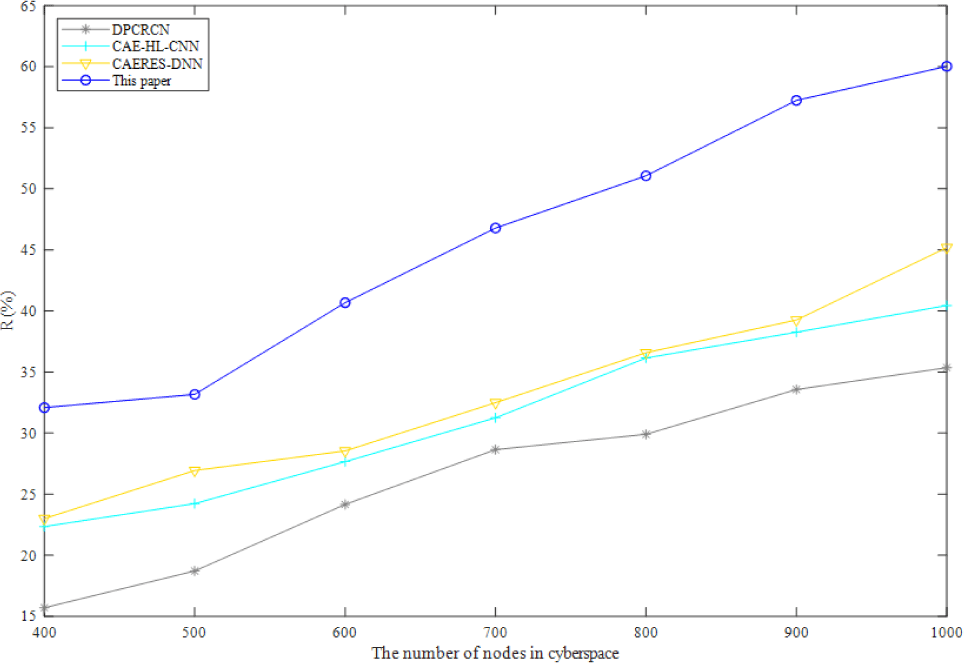
In complex-heterogeneous cyberspace, Fig. 2 depicts the variation of recall ratio of four algorithms. As shown in Fig. 2, the recall of the method presented in this study is greater than that of the other three baselines, and it rises as the number of cybernetic nodes rises. In a fully connected DNN structure, connections may be made between the bottom neurons and all of the higher neurons of the other three baselines, increasing the number of parameters and lowering the recall. After dimensionality reduction, the benefits of the method suggested in this study become more apparent when applied to cartographic data in complex-heterogeneous cyberspace.
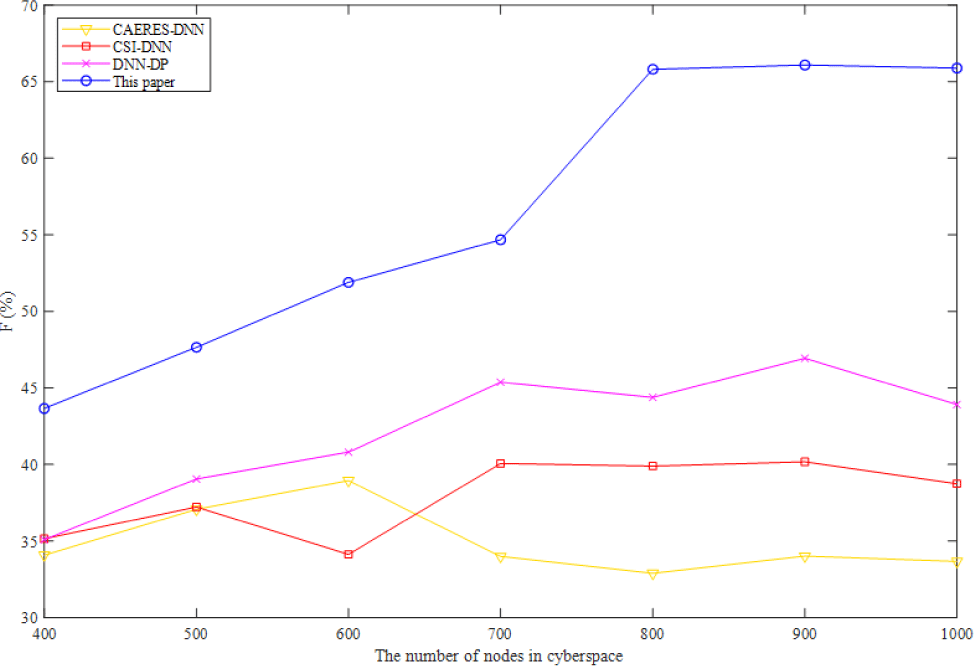
The F1 score of four algorithms for visualizing complicated heterogeneous cyberspace is shown in Fig. 3. Precision and recall should be as high as feasible when assessing the simulation results. However, in most situations, the two ratios contradict one another. Therefore, the two ratios should be taken into account using the F1 score, which can provide an overall indication of the method's efficacy. I find that the F1 score is greatest for the approach described in this work, followed by DNN-DP, CSI-DNN, and CAERES-DNN. Despite the CSI-DNN's high F1 score and poor precision ratio, keeping features invariant to the investigated impairments is the algorithm's stated goal.
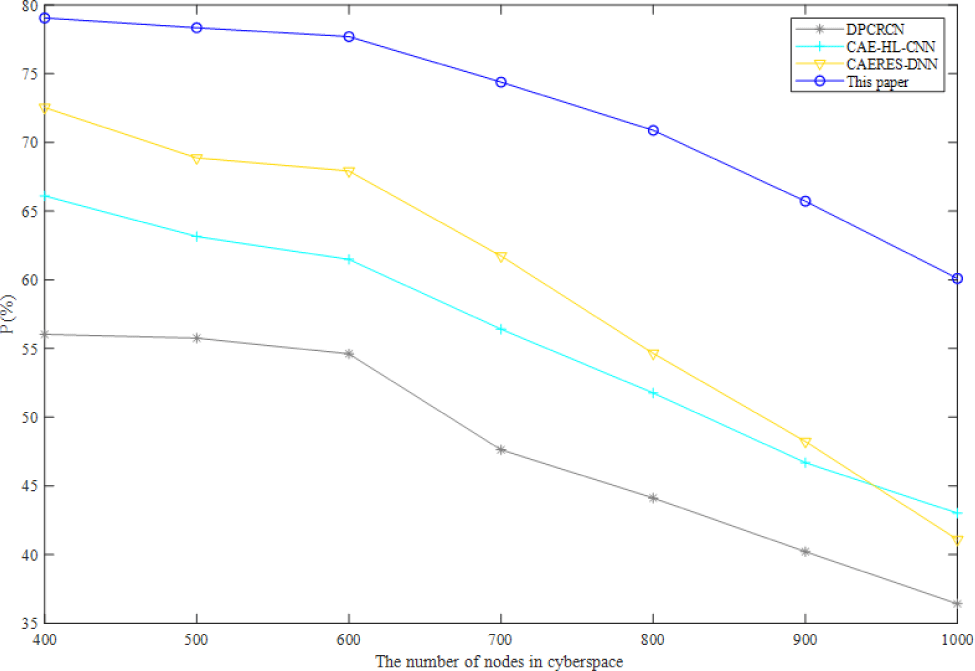
In order to verify the proposed method in this paper has a good performance in DNN based complex-heterogeneous cyberspace cartographic visualization. The other neural network algorithms are selected for comparison, which are convolutional auto-encoders and hinge loss CNN (CAE-HL-CNN) [40] and dual path CNN-recurrent neural network (RNN) cascade network (DPCRCN) [41].
As can be seen from Fig. 4, Fig. 5, and Fig. 6, the precision ratio, recall ratio and F1 score of the proposed method are the highest comparing with other three neural network algorithms. CNN and RNN are essentially different though they can conduct sequence modeling. RNN has an order in time dimension, and the order of input will affect the output. CNN mainly obtains the overall information from local information aggregation and extracts the hierarchical information from the input layer. The convolution kernel of CNN emphasizes the window in space, which is similar to the time series problem, but RNN does not consider the spatial cases. The proposed method firstly reduces the dimensionality of high-dimensional data to avoid the pressure of processing high-dimensional data. Although DNN cannot process the changes in time series, the proposed method based on spatiotemporal data modeling which can effectively reduce the impact of the changes in time series.
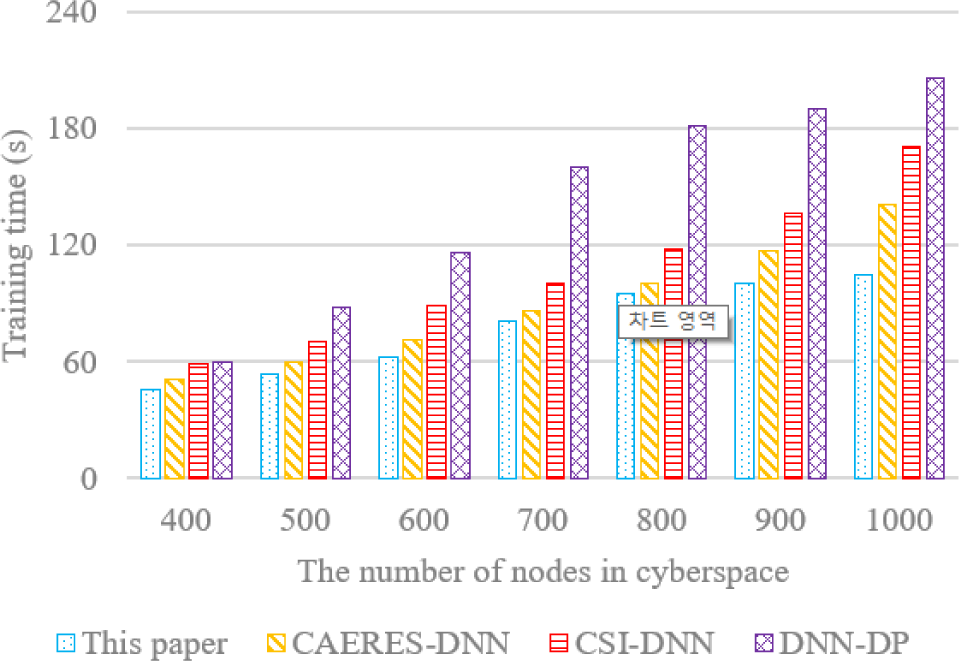
Four DNN-based algorithms are used in training time comparison, and the training time comparison of this paper, CAERES-DNN, CSI-DNN and DNN-DP is reported in Fig. 7. With the increasing number of nodes in complex-heterogeneous cyberspace, the training time for forecasting the risk distribution of network security event is also growing. Even with the growing number of nodes in cyberspace, the training time is surprisingly close to two minutes. With 800 nodes, the training time only increases by a little range, demonstrating the method's superior convergence performance. ReLU activation function is used in this paper, and momentum optimization is added to make the model jump out of locally optimal easily, which is also reduce oscillation and accelerate convergence speed.
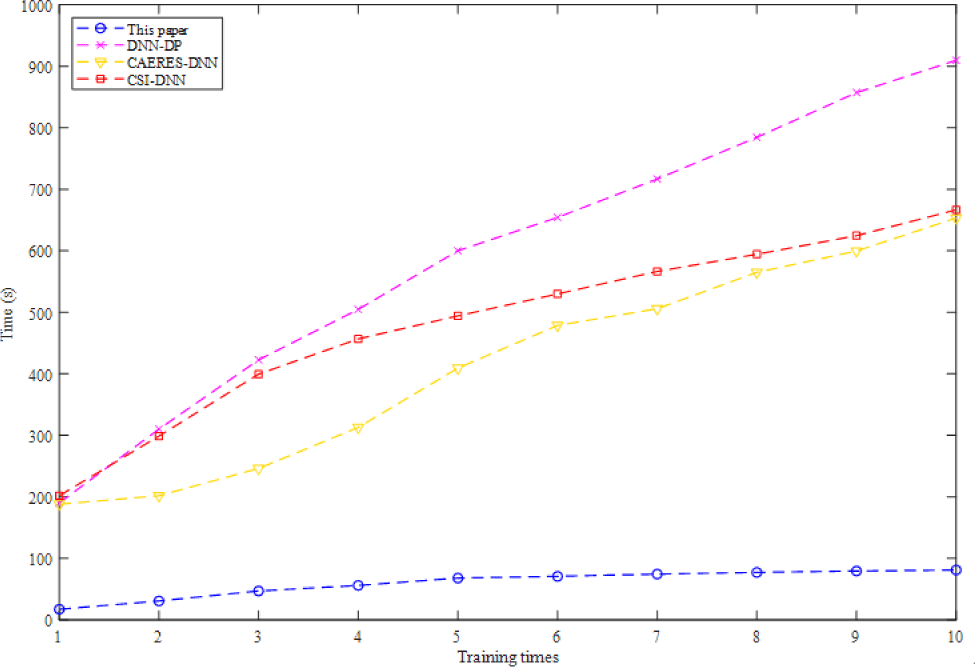
LLE is used to reduce the data dimensionality in order to avoid increasing the training time of high-dimensional data. In this paper, a certain number of samples are used to form a Mini-batch. It is obviously that the proposed method using Mini-batch has a good performance in running time, which is decreased by orders of magnitude. The Mini-batch used in this paper is a small part of training dataset. The data is divided into several groups, and parameters are updated according to the batch. In this way, data in batch jointly determines the direction of the gradient, so it is hard to deviate during descent and randomness is reduced. On the other hand, the number of batch samples is much smaller than the whole dataset, and the computation is not very large, which also reduces the running time (Fig. 8).
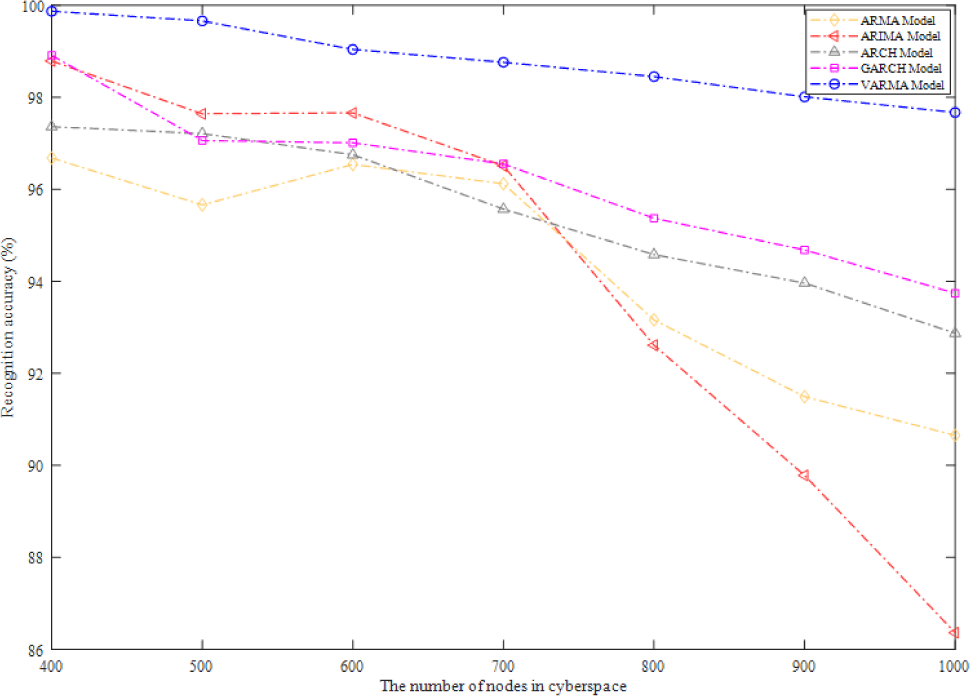
Data in complex-heterogeneous cyberspace mainly includes coordinates and other data such as application, IP and subject of network, if the data movement or data fault happens in data modeling, the selected model must recognize movement and fault in time. As shown in Fig. 9, VARMA model has a relatively average fault recognition accuracy, which is also the highest, because it is analyzed and modeled from both spatial and temporal attributes in complex-heterogeneous cyberspace. The recognition accuracy of ARMA model is relatively the lowest, but it performs well when the number of nodes ranges from 600 to 700. When the number of nodes is less than 800, the recognition accuracy of ARIMA model is better than that of ARMA model, but when the number of nodes is more than 800, the recognition accuracy of ARIMA Model is suddenly lower than 90%. While the recognition accuracy of ARCH model and GARCH model is stable at more than 90%.
Additionally, we compare the visualization results using the GARR from the internet topology zoo. GARR is Italy's national research and education network, which stands for "Gruppo Armonizzazione Reti della Ricerca" (Italian for Research and Education Network Harmonization Group). It provides high-performance network connectivity and advanced services to the academic and research community in the country. GARR provides its users with a wide range of services, including high-speed internet connectivity, videoconferencing, cloud computing, virtual private networks, and access to e-learning platforms. Fig. 10 shows the visualization results of the four methods on GARR. The visualization result of DNN-DP, which exhibits no operations on nodes and edges, suggests a streamlined and concise representation. This can be advantageous for situations where simplicity and clarity are prioritized, allowing for a more focused understanding of the network's structure. In contrast, CAERES-DNN adjusts the weight of edges in its visualization result. This adjustment likely highlights the significance or relevance of certain connections within the network. By assigning different weights to the edges, the visualization can emphasize essential relationships and provide insights into the network's functional dynamics. Meanwhile, CSI-DNN ranks nodes by latitude in its visualization result. This arrangement based on latitude can introduce a geographical context, potentially aiding in interpreting network components and their spatial relationships. This approach might be beneficial in scenarios where geographic factors play a role, such as studying regional network connectivity or assessing network vulnerabilities across different locations. The method proposed in the paper achieves a relatively full visualization result, which effectively captures the complex heterogeneous nature of the GARR network. The proposed approach demonstrates a comprehensive representation that incorporates multiple aspects of the network's structure and behavior by utilizing techniques such as LLE for dimensionality reduction and vector ARMA for spatiotemporal data modeling. The visualization results presented in Fig. 10 highlight the diverse perspectives and visualization effects achieved by the different methods. By showcasing the unique contributions of the proposed method in achieving complex heterogeneous cyber cartographic visualization, the paper establishes its originality and potential value in the cyber security and safety applications field.
This paper uses LLE as a dimensionality reduction technique for training cartographic coordinates data. In the following, we compare LLE with PCA, t-SNE, and Isomap regarding reconstruction error, neighborhood preservation, visualization quality, and computational efficiency. PCA is a linear technique that focuses on capturing the maximum variance in the data, while t-SNE and Isomap aim to preserve the global and local structures, respectively. Reconstruction error measures how well the reduced-dimensional data can be reconstructed back to the original high-dimensional space. It quantifies the loss of information during the dimensionality reduction process. Lower reconstruction error indicates better preservation of the original data. Neighborhood preservation: Since LLE aims to preserve the data's local structure, evaluating the nearest neighbors' preservation is essential. Visual assessment becomes crucial if the purpose of dimensionality reduction is to facilitate visualization. Moreover, the computational complexity of the dimensionality reduction techniques should also be considered, especially for large-scale datasets.
Table 1 shows the comparison of dimensionality reduction. The reconstruction error for PCA was calculated as the sum of squared differences between the original and reconstructed data using the first two principal components. The neighborhood preservation score for t-SNE was calculated using the k-nearest neighbor graph with k=10. The reconstruction error for PCA was calculated as the sum of squared differences between the original and reconstructed data using the first two principal components. The neighborhood preservation score for t-SNE was calculated using the k-nearest neighbor graph with k=10. The reconstruction error for Isomap was calculated as the difference between the geodesic distances in the high-dimensional and low-dimensional spaces. The reconstruction error for LLE was calculated as the sum of squared differences between the original and reconstructed data in the high-dimensional space. In this example, LLE outperformed PCA regarding reconstruction error and neighborhood preservation, consistent with its ability to capture nonlinear relationships and preserve the local structure. Isomap also performed well regarding reconstruction error and neighborhood preservation, but LLE needed to be more computationally efficient. t-SNE strongly preserved the local neighborhood structure but did not have an explicit reconstruction error. In terms of visualization quality, all techniques can produce high-quality visualizations depending on the specific goals and characteristics of the data. Therefore, visual inspection of the plots may also be an essential metric for evaluating the effectiveness of the different techniques. By evaluating these metrics, it can be determined that LLE is suitable for complex heterogeneous cyber cartographic visualization.
V. CONCLUSION
This paper studies complex-heterogeneous cyberspace cartographic visualization. At first, we use LLE to reduce the data dimensionality. Then, a certain number of data samples are used to form a Mini-batch, and data after dimensionality reduction is trained in DNN. At last, in terms of temporal and spatial, we design the data model in order to realize cartographic visualization. Furthermore, the proposed method is simulated based on cyberspace datasets available on data.world, and the comparison experiments demonstrate that the proposed method is outperforming in precision ratio, recall ratio, F1 score, training time and recognition accuracy.
Although the proposed method has a good performance in training time comparing with the baselines. However, it is generally slow to train large DNN networks. In the future, we can find a network that can accomplish similar tasks, and then use part of its shallow network and parameters to perform simple extraction of input features, that is, transfer learning, which can not only speed up the training speed, but also require less training data.