Journal of Multimedia Information System

Korea Multimedia Society

J Multimed Inf Syst 10(4):351-360

eISSN: 2383-7632

DOI: https://doi.org/10.33851/JMIS.2023.10.4.351

Section C

Machine Learning-Based Work Efficiency Monitoring Method for Student Supervisor

Yuzhou Ke¹^,^*

¹College of Business Administration, Guangdong Baiyun University, Guangzhou, China, yangjie06_cc@163.com

^*Corresponding Author: Yuzhou Ke, +86 15802036068, yangjie06_cc@163.com

© Copyright 2023 Korea Multimedia Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Nov 23, 2023; Revised: Dec 09, 2023; Accepted: Dec 11, 2023

Published Online: Dec 31, 2023

Abstract

As student supervisor workloads increase, ensuring efficient support is challenging. A novel machine learning method using clustering analysis is proposed to gain insights into time allocation and identify optimization opportunities. Specifically, a covariance distance measure analysis approach is presented for characterizing the closeness of data items in multi-dimensional cluster analysis through efficient distance measuring. The membership degree of each sample point is first determined concerning class characteristics through the fuzzy c-means approach, which involves first assigning weights to data items. Then, the membership degree is used to determine the degree of dissimilarity between the samples. Finally, the covariance distance measurement between sample points is used as the second optimization criterion to distinguish between data types, and the optimal solution is calculated iteratively by alternating fixed variables to optimize the clustering metric and the distance measurement learning parameters and produce more accurate clustering results. The experimental findings on datasets demonstrate that the proposed approach outperforms benchmarks in terms of clustering accuracy. Therefore, the high clustering accuracy empowers the student supervisor to make informed decisions about time allocation, allowing them to optimize their efforts and resources.

Keywords: Clustering Analysis; Student Supervisor; Fuzzy c-Means; Covariance Distance Measurement; Work Efficiency Monitoring

I. INTRODUCTION

In colleges, student supervisors guide and mentor their peers through various educational and professional challenges [1]. Whether they assist with research projects, provide academic support, or manage extracurricular activities, student supervisors are key facilitators in creating a conducive learning environment. Student supervisors must prioritize work efficiency to maintain a productive and supportive atmosphere [2-3]. Student supervisors often possess advanced knowledge and experience within a particular field, making them ideal candidates to support their fellow students. They act as mentors, motivators, and role models, fostering an inclusive and collaborative learning environment. Efficiency is paramount for student supervisors, as it directly influences the quality and effectiveness of their guidance. Optimizing their productivity with a limited amount of time and resources ensures they can handle their responsibilities effectively while maintaining a healthy work-life balance. Student supervisors may encounter various challenges that hinder their efficiency. These challenges could include heavy workloads, time constraints, interpersonal dynamics, and balancing their academic commitments alongside supervisory roles. A student supervisor’s work efficiency significantly impacts their ability to support and guide their peers effectively. By embracing time management, effective communication, delegation, continuous learning, and self-care, student supervisors can optimize their performance and contribute positively to the growth and development of their academic community [4].

Adequate student supervision is essential in ensuring college students receive the necessary guidance and support to succeed academically and personally. To maintain a high standard of support and ensure optimal student outcomes, it is crucial to monitor the work efficiency of student supervisors. Work efficiency monitoring for student supervisors is a systematic approach to evaluate their performance, effectiveness, and adherence to best practices in academic advising and mentoring [5-6]. Monitoring work efficiency helps identify areas where student supervisors can improve student support, leading to more personalized and practical guidance. Adequate supervision positively impacts student retention rates and academic success, as students are more likely to persist when they receive proper support and mentoring.

The widespread application of machine learning can potentially revolutionize various industries, including education [7]. In the context of student supervision in colleges, machine learning can play a significant role in monitoring and optimizing the efficiency of student supervisors. Utiliz- ing clustering analysis to group tasks and activities per- formed by student supervisors based on their similarity is an excellent approach to gain insights into their time allocation and identify potential areas for optimization [8-9]. Clustering analysis refers to grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar to each other than to those in other groups [10]. Utilizing clustering analysis to group tasks and activities performed by student supervisors based on their similarity can be a powerful tool for optimizing time usage and improving the efficiency of college student supervision processes. By gaining insights into time allocation patterns, colleges can make data-driven decisions to enhance student support and foster a more effective learning environment. Therefore, to select a more effective distance measurement method to improve the clustering quality, a covariance distance measure (CDM) analysis is proposed in this paper. Consequently, the main contributions of this paper are listed as follows.

This paper introduces a new method that utilizes machine learning techniques for monitoring the work efficiency of student supervisors. This method addresses the challenge of efficiently and personally supporting a growing number of students under their supervision.
This paper uses clustering analysis to group tasks and activities student supervisors perform based on their similarity, allowing for insights into how the supervisors allocate their time, and help identify potential areas for optimization.
This paper introduces a covariance distance measurement analysis approach to characterize the closeness of data items in multi-dimensional cluster analysis. This efficient distance measurement analysis is applied to enhance the clustering process and produce more accurate results.
This paper employs the fuzzy c-means to determine the membership degree of each sample point concerning class characteristics, involving assigning weights to data items, which helps assess the degree of dissimilarity between samples and optimize the clustering metric.

The rest of this paper is organized as follows. Section 2 reviews the related works. In Section 3, the distance measurement model is studied. The CDM algorithm is proposed in Section 4. The experimental results and analysis are presented in Section 5, and Section 6 concludes this paper.

II. RELATED WORKS

Work efficiency monitoring methods aim to assess and optimize the productivity and effectiveness of individuals, teams, or organizations in accomplishing their tasks and goals. These methods encompass various techniques, tools, and approaches to gather data, analyze performance, and provide insights for improvement [11-14]. Project management allows teams to organize and track tasks, assign responsibilities, set deadlines, and monitor progress, providing visibility into project status and identify bottlenecks or areas needing improvement [15]. Key Performance Indicators are measurable metrics that represent specific performance goals. They can include individual or team targets related to productivity, quality, customer satisfaction, or other relevant aspects [16]. Gamification techniques integrate game elements into work tasks to increase motivation and engagement [17]. Leaderboards, badges, and rewards are gamification elements that encourage productivity. Regular surveys and feedback sessions help collect insights directly from employees. Understanding their perceptions and challenges can highlight areas where efficiency improvements are needed [18].

AI and machine learning can be employed to analyze large datasets, predict workflow patterns, and optimize resource allocation [19-20]. These techniques can identify patterns of inefficiency and provide personalized recommendations. It is important to note that work efficiency monitoring should be approached with sensitivity to privacy and ethical considerations. Balancing productivity monitoring with employee well-being and trust is crucial to maintain a positive work environment. Additionally, each organization may adopt different methods based on its specific goals, industry, and work dynamics. Student supervision is a critical aspect of education and academic development. Educational institutions and supervisors employ several existing approaches and methods to support and guide students effectively. Machine learning has various applications in work efficiency monitoring, enabling organizations to gather insights, identify patterns, and optimize productivity.

Sometimes, adaptive selection/weighting of features is typically used for dimensionality reduction and performance improvement. The features with low correlation [21] and high discrimination [22] should be selected and given high weights.

III. DISTANCE MEASUREMENT MODEL

The research focus of clustering analysis is to use an effective distance measurement method to analyze the discreteness or dissimilarity of information between data objects for data classification.

3.1. Fuzzy Clustering Model for Euclidean Distance

The fuzzy c-means (FCM) clustering algorithm, initially proposed by J.C. Dunn in1973 and further developed by J.C. Bezdek in 1981, was employed to categorize task efficiency without modification, as it is well-suited to the data structure encountered in this study [23]. FCM is a soft clustering method that allows data points to belong to multiple clusters with varying degrees of membership. Let X represent the input data. C is a set of k center, denoted as $C = {c a | c a ∈ R P} a = 1 k$ , and M is a matrix, denoted as $M = {m j a | m j a ∈ R}$ . In this context, the variable k denotes the number of clusters, whereas each m_ja signifies the membership value of the data point x_j in cluster a. The FCM’s objective function is expressed as follows.

min M, C ∑ j = 1 n ∑ a = 1 k m j a f ‖ x j − c a ‖ 2 .

(1)

The variable f denotes the degree of ambiguity, whereas the expression $‖ x j − c a ‖ 2$ indicates the Euclidean distance [24], quantifying the extent of dispersion across data points. A non-convex nature characterizes the optimization issue represented by Eq. (1), as it involves a double convex objective function. The utilization of alternate optimization strategies may effectively address this type of problem. When the value of C is constant, the relationship between C and M is convex. Similarly, the relationship between C and M is also convex when the M value is constant. The problem is first optimized over another parameter by considering C to be fixed. Then the process is repeated for M until convergence is achieved, updating the Equation as follows.

{m j a ′ = 1 ∑ a = 1 k (‖ x j − c a ′ ‖ 2 ‖ x j − c a ‖ 2) 1 (f − 1) c a = ∑ j = 1 n m j a f x j ∑ j = 1 n m j a f .

(2)

In the fuzzy c-means algorithm, weights are assigned to each data point based on its degree of membership to different clusters. The membership degree values represent fuzzy weights reflecting how strongly a data point belongs to each cluster. For a data point x_j, its membership degrees to all clusters will be 1. A higher m_ja indicates x_j is more associated with cluster c_a. These membership weight values are initialized randomly and then updated iteratively using the optimization steps outlined in Eq. (2). The updated weights determine the cluster centers via weighted averaging. Thus, the weighting process helps quantify the relative association of data points to different clusters, which gets refined over iterations to produce the final clustering result.

3.2. Classification Distance Measurement Model

All numerical values and classification distance measurement used by the cluster analysis.

d → (x j, x k) = [d (x j, 1, x k, 1), ⋯, d (x j, u, x k, u) d (x j, u + 1, x k, u + 1), ⋯, d (x j, u + v, x k, u + v)] T .

(3)

The variables x_j, and x_k denote the vectors representing the distances between two points in a point-to-point context. The variables u and v denote the number of class and numeric properties, respectively.

The overlap distance, denoted as d_o, and the αMax+βMin distance, denoted as d_f, are defined as follows for each p ∈{1,⋯,u} [25].

d o (x j, p, x k, p) = {0, i f x j, p = x k, p 1, i f x j, p ≠ x k, p .

(4)

d f (x j, p, x k, p) = {0, i f x j, p = x k, p 1 − A p (A p + 3), i f x j, p = x k, p .

(5)

A_p is a numeric attribute with different values for the pth attribute.

d (x j, p, x k, p) = x j, p − x k, p .

(6)

The following equation describes the distance between the point x_j and the cluster c_a.

d →' (x j, x k) = [d →' (x j, 1, c a, 1), ⋯, d →' (x j . u, c a . u) d →' (x j, u + 1, c a, u + 1), ⋯, d →' (x j, u + v, c a, u + v)] T .

(7)

3.3. Mahalanobis Distance (Covariance Distance Measurement) Modeling

For the cluster analysis of multi-dimensional feature space, an effective distance measurement method must represent the correlation between data attributes. Sets that are the same and sets that are different are shown by the terms S and D, respectively. While traditional fuzzy c-means clustering is utilized, the novel contribution lies in integrating a covariance distance measure, which enhances the algorithm’s sensitivity to the multidimensional nature of data.

S = {(x j, x k) | x i and x j are the same class} .

(8)

D = {(x j, x k) | x i and x j are the different class} .

(9)

The maximally separable definition of the distance measure postulates that x_j and x_k should exhibit proximity if they are members of set S while demonstrating distinctness if they are members of set D. In the linear methodology, the data is transformed into a novel space denoted as T, where each data point x_j is mapped to x_k by acquiring a linear transformation. The linear approach involves acquiring a linear transformation, subsequently used to project the data into a novel space denoted as T:x_j ← x_k. This is a way to show the Mahalanobis distance, which is a way to measure correlation distance in the projected space [26].

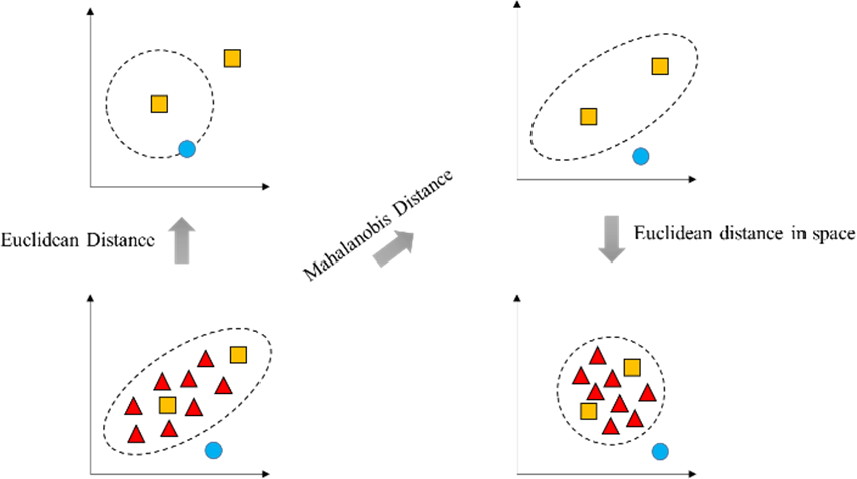
In contrast to the Euclidean distance, the Mahalanobis distance (covariance distance measurement) is an unsupervised metric learning method that characterizes the correlation between attributes and is scale-independent, as shown in Fig. 1.

Fig. 1. Euclidean distance and Mahalanobis distance.

Download Original Figure

The orange points, blue points, and green points in Fig. 1 represent various sample points to illustrate the difference between Euclidean and Mahalanobis distances. Observe the distance between the two orange points in Fig. 1 and the center orange to the blue point. If the data distribution is not considered, the blue color is closer, which is the Euclidean distance measurement. However, the effect of data distribution needs to be considered in practice. The data samples are elliptical, with blue points outside and orange points inside the ellipse, so the two orange points are closer. The Mahalanobis distance (covariance distance measurement) measure can effectively characterize the proximity between data objects [27]. In contrast, the Euclidean distance measure obtains the degree of dispersion between the data, which is not conducive to analyzing the correlation between multidimensional data.

IV. CDM ALGORITHM

Traditional FCM does not define data closeness precisely, as it employs a fuzzy representation. Let the fuzzy affiliation matrix be represented by $M = {m j a | m j a ∈ R}$ , where m_ja is a real number. d_jk′ is the degree of difference between the data points j and k, which is computed by the fuzzy affiliation value.

d j k ′ = 1 − m j m k T (‖ m j ‖ 2 × ‖ m k ‖ 2),

(10)

where m_j and m_k are rows j and k of matrix M, which are quantitatively estimated by whether the membership is similar based on the similarity S between data points j and k. If the data belongs to different clusters, all clusters (m_j and m_k) have different values. m_j and m_k have different pairs of associated entries (m_ja and m_ka), at least one of which is close to zero. Therefore, their degree of difference d_jk′ is close to 1.

To maximize class separation, covariance distance is used instead of Euclidean distance to improve the optimization problem of fuzzy clustering [28]. One of the criteria used to quantify this expectation is the minimal distance between all comparable data points. In the context of clustering, it is essential to note that all data points inside a given cluster S, denoted as x_j and x_k, are viewed as paired and undergo migration towards the cluster center c_a. Since S is a fuzzy similarity set, this constraint must be fulfilled following the membership m_ja assigned to x_j in cluster a. To accomplish this purpose, the Euclidean distance in the objective Eq. (1) of the FCM model is substituted with a covariance measurement. The initial criteria are stated in the form of a loss function.

min M, C ∑ j = 1 n ∑ a = 1 w m j a f d → ′ (x j, c a) T d → ′ (x j, c a) .

(11)

Therefore, the issue at hand is resolved in the following manner.

min M, C (1 − β) min M, C ∑ j = 1 n ∑ a = 1 w m j a f d →' (x j, c a) T d →' (x j, c a) + β ∑ J = 1 n ∑ K = 1 n d j k' ζ j k . s . t . {d → (x j, x k) T D d → (x j, c a) ≥ δ − ζ j k, ∀ j, k ∈ (1, ⋯, n) ζ j k ≥ 0 δ > 0 0 < ∑ j = 1 n m j a < n ∑ a = 1 w m j a = 1 .

(12)

The symbol β represents a compromise parameter that balances two components. ζ_jk is introduced as the slack variable, and δ is denoted as the minimal distance. It is a constant value greater than zero. The symbol D denotes a semi-definite matrix, with the condition that D is more significant than or equal to zero. In the context of the optimization problem, it may be stated that when the value of d_jk′ is equal to zero, the corresponding term in the problem also evaluates to zero. Conversely, when the value of d_jk′ is equal 1, the corresponding ζ_jk value contributes to the second term.

The fuzzy c-means algorithm assigns a membership degree m_ja to each data point x_j representing its association with cluster c_a These membership values are used as fuzzy weights that quantify the degree to which data points belong to different clusters. Data points may have partial membership in multiple clusters, with the sum of memberships equal to 1.

For the proposed covariance distance metric learning approach, these membership weights m_ja play a key role in the optimization function. The weighted covariance distance d′(x_j, c_a between a data point x_j and cluster center c_a is calculated using the corresponding membership degree m_ja as:

d' (x j, c a) = m j a f * (x j − c a) ′ D (x j − c a) .

(13)

Additionally, the membership weights determine the difference degree d_jk′ between two data points, x_j, and x_k, based on the similarity of their membership distributions. The difference degree is an optimization criterion to ensure separation between dissimilar points.

Thus, the membership weights m_ja from fuzzy c-means provide a means to quantify association to clusters when learning the distance metric D. The weights help ensure that the optimization process results in tighter clustering of similar data points.

The application of FCM is different from k-means, which provides clear label information and adjusts the transformation matrix to fit the clustering index by learning the clustering index. In the subsequent iteration, the clustering index will retain its prior value, indicating a local optimization phenomenon in this approach. Furthermore, the update iteration fails to acquire knowledge of the new transformation matrix, leading to a rapid convergence towards the local optimum issue [29]. The data points in FCM are somewhat similar or different. The satisfaction degree of the two criteria in equation (12) can be obtained according to the fuzzy membership value m_ja and difference degree d_jk′, avoiding convergence to the local optimal.

V. EXPERIMENT AND RESULTS ANALYSIS

5.1. Environment and Method

To verify the proposed algorithm, the two datasets, Wine and Breast Tissue (BT), from the UCI machine learning repository are selected as the benchmark [30]. The datasets selected for the study are chosen to benchmark the proposed machine learning method’s efficiency in a controlled environment before its application in monitoring the work efficiency of student supervisors. Table 1 presents an overview of these datasets. The BT dataset has nine features and 106 instances, each described by nine features representing electrical impedance measurements of breast tissue samples. These are categorized into six classes based on tissue type. The attributes are numerical and continuous, derived from various impedance measurements in different frequencies, which are analogous to different performance metrics that could be observed in supervisory roles. The Wine dataset has 13 features and 178 instances; each instance is characterized by 13 features, reflecting chemical analyses of Italian wines grown in the same region but derived from three different cultivars. The attributes of the Wine dataset are also numerical and continuous, covering a range of chemical properties like alcohol and malic acid content. These can be compared to various evaluative measures in a supervisory context.

Table 1. Dataset information.

Datasets	Number of instances	Number of attributes	Number of categories
Breast tissue	106	9	6
Wine	178	13	3

Download Excel Table

Both datasets possess a mix of features that mirror the variety and complexity of data one would expect in work efficiency monitoring for student supervisors. The ‘Number of Features’ in both datasets aligns with the diverse metrics for assessing supervisors’ performance. ‘Dimensionality’ reflects the varied nature of supervisory tasks, and the ‘Nature of Attributes’ represents different quantitative assessments that a supervisor may evaluate. Through the use of these datasets, it is able to demonstrate the accuracy and reliability of the clustering approach, providing a solid indication of its applicability to real-world supervisory data.

The datasets detailed in Table 1, while not derived from student supervisor scenarios, have been selected for their structural complexity and attribute diversity, which align closely with the data types anticipated in supervisory monitoring contexts. The BT dataset, with 106 instances across nine attributes and six categories, and the Wine dataset, comprising 178 instances, 13 attributes, and three categories, exemplify multifaceted data similar to that which would be analyzed in the supervisory role. The ‘Number of instances’ represents the volume of supervision scenarios, the ‘Number of attributes’ corresponds to the various performance metrics of student supervisors, and the ‘Number of categories’ reflects the potential classifications of supervisory activities. These datasets are utilized to validate the robustness of the proposed clustering algorithm and simulate its performance in categorizing and analyzing the efficiency of supervisors’ tasks. Through this simulation, the algorithm’s potential efficacy in real-world applications is demonstrated, laying the groundwork for subsequent application to data directly collected from student supervisor activities.

The simulation experiment entailed comparing the predicted and actual labels of each data point to evaluate the accuracy of the clustering results. Two simulation measures, namely clustering accuracy and normalized mutual information (NMI), are employed to compare various techniques [31].

The evaluation of clustering accuracy entails the evaluation of the accuracy of data point allocation by quantifying the number of correctly assigned data points and dividing it by the total number of data points.

NMI is often used in clustering evaluation, community detection, and information retrieval tasks. There needs two clusterings to calculate Normalized Mutual Information: the ground truth (true clustering) and the predicted clustering. Let us denote the true clustering as T and the predicted clustering as P. Both T and P should be arrays or lists of cluster assignments, where each element represents the cluster assignment of a data point. Here are the steps to calculate NMI.

Step 1: Calculate the entropy of the true clustering H(T).

H (T) = − ∑ ​ (count_t n) * log 2 (count_t n),

(14)

where variable count t represents the quantity of data points included within cluster t of the true clustering, whereas n is the overall amount of data points.

Step 2: Calculate the entropy of the predicted clustering H(P).

H (P) = − ∑ ​ (count_p n) * log 2 (count_p n),

(15)

where variable count p represents the count of data points within cluster p in the anticipated clustering, whereas the variable p represents the overall count of data points.

Step 3: Calculate the mutual information (MI) between the true and predicted clusterings.

M I (T, P) = ∑ ​ ∑ ​ (count_t p n) * log 2 ((n * count_t p) count_t * count_p),

(16)

where variable count_tp represents the count of data points that belong to cluster t in the real clustering and cluster p in the predicted clustering. The variables count t and count p are defined in steps 1 and 2, respectively. The variable n represents the total number of data points.

Step 4: Calculate the NMI.

N M I = 2 * M I (T, P) H (T) + H (P) .

(17)

The NMI score is between 0 and 1. A value closer to 1 indicates a higher similarity between the two clusterings, while a value closer to 0 indicates a lower similarity.

5.2. Performance Analysis

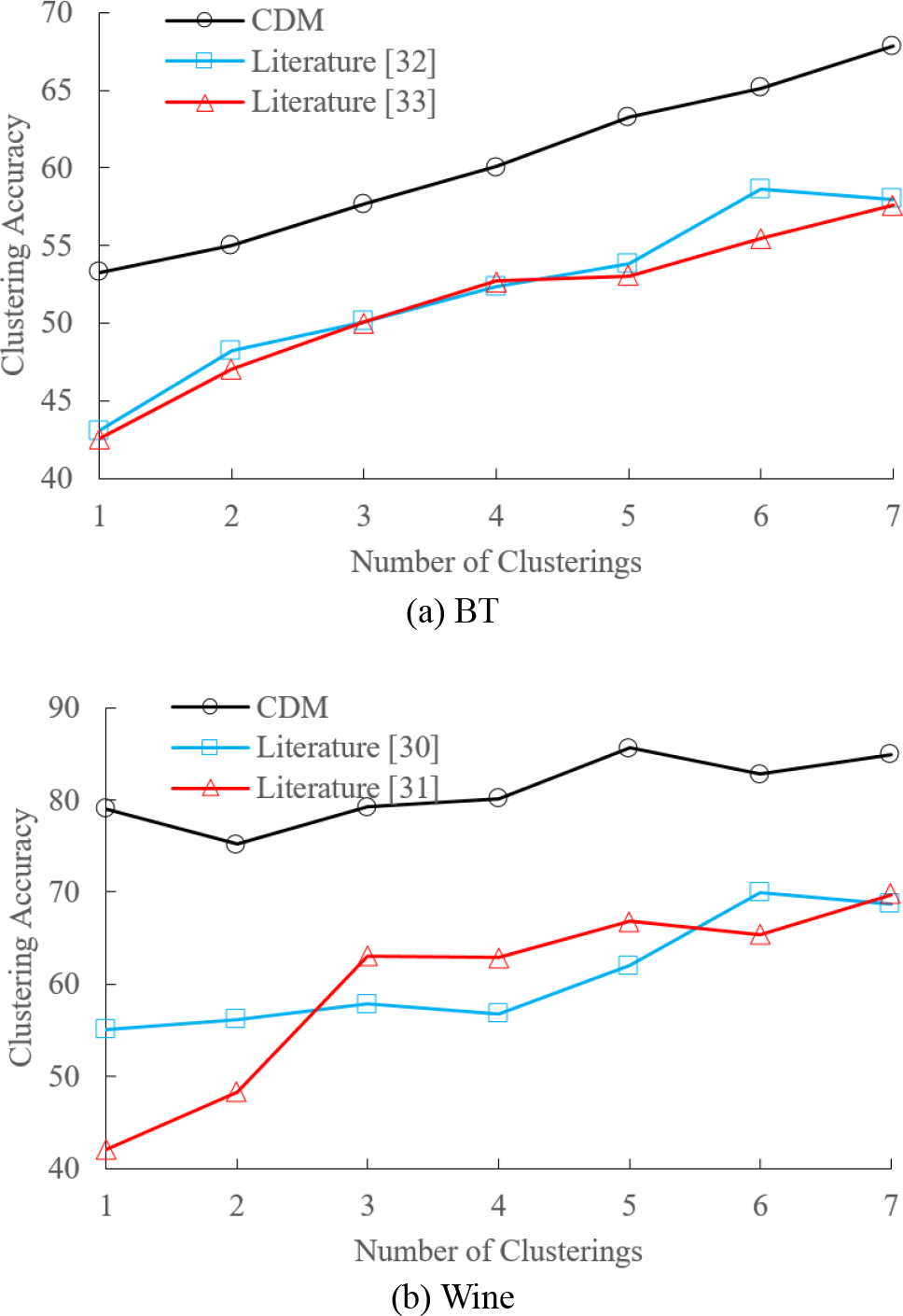
The accuracy results of CDM, literature [32], and literature [33] are assessed in the BT and Wine datasets to examine the impact of cluster quantity on clustering outcomes. After determining that the number of classes is equal to the number of clusters, the number is increased by a factor of four. Fig. 2 displays the simulation results.

Fig. 2. Clustering accuracy.

Download Original Figure

Fig. 2 shows the algorithm’s performance in two datasets, and the clustering accuracy of the three algorithms is gradually improved with the increasing number of clusters. The clustering accuracy of the CDM algorithm is better than that of the contrast algorithm in the BT dataset. Compared with literature [32] and literature [33], the clustering accuracy of the CDM algorithm in the Wine dataset fluctuates around 80%, which can maintain stable and high-precision clustering performance.

High clustering accuracy in work efficiency monitoring for student supervisor’s aids in pinpointing areas of excessive or insufficient time allocation. Precise clustering of students based on needs and performance patterns provides valuable insights for supervisors in understanding resource allocation. Accurate clustering uncovers student groups requiring additional attention and support, including struggling students or those facing specific challenges. Identifying these groups allows supervisors to allocate more time and resources for adequate assistance.

On the other hand, high clustering accuracy can also reveal student groups performing well and requiring less intervention or supervision. These groups may be self-driven and demonstrate higher levels of independence. By recognizing these time-efficient groups, the supervisor can focus more on other areas that need attention. High clustering accuracy can highlight imbalances in time allocation across different student groups. It can help the supervisor ensure that each group receives appropriate attention and support, leading to a more equitable distribution of their efforts.

Additionally, accurate clustering allows the student supervisors to manage their time proactively. They can identify potential time sinks and areas requiring additional support before issues become critical. This proactive approach can help avoid wasted time and effort on reactive measures. Over time, the student supervisor can continuously evaluate the effectiveness of their time allocation strategies based on clustering results. This iterative improvement process ensures the supervisor can fine-tune their time management techniques for better work efficiency. High clustering accuracy gives the student supervisor data-driven evidence to support their time allocation decisions. It ensures that decisions are based on student needs and performance, leading to more effective use of time and resources. In summary, high clustering accuracy empowers the student supervisor to make informed decisions about time allocation, allowing them to optimize their efforts and resources. By identifying areas of excessive or insufficient time usage, the supervisor can tailor their approach, improve work efficiency, and ultimately enhance the learning experience for students.

VI. CONCLUSION

This paper studies machine learning-based work efficiency monitoring method for student supervisors, and the summary is as follows.

This paper proposes a novel machine learning method for monitoring student supervisor work efficiency using clustering analysis of activities based on similarity.
A covariance distance metric learning approach is introduced to improve clustering accuracy by considering attribute correlations when measuring proximity.
Fuzzy c-means is utilized to assign membership weights to data points, reflecting their association to clusters during optimization.
The method demonstrates superior clustering accuracy compared to benchmarks on real-world datasets.
Accurate clustering of supervisor activities provides data-driven insights to tailor time allocation, enhance work efficiency, and improve student guidance.

Despite the promising results, the research also acknowledges certain limitations. One limitation is the dependency on the availability and quality of data. To further enhance the robustness of the proposed method, efforts should be made to gather more comprehensive and diverse datasets from different educational settings. Additionally, the proposed algorithm may have certain constraints regarding the scalability to handle massive datasets. Future research should optimize the algorithm’s performance to handle more extensive and complex data, ensuring its practical applicability in real-world scenarios.

REFERENCES

[1].

J. F. Du, X. M. Chen, and Y. G. Dou, “Evaluating the practical effectiveness of college counselors’ ideological and political education using big data video streaming,” Wireless Networks, vol. 26, no. 1, p. 2023.

[2].

A. Campbell, S. R. Vance, and S. L. Dong, “Examining the relationship between mindfulness and multicultural counseling competencies in counselor trainees,” Mindfulness, vol. 9, pp. 79-87, Jan. 2018.

[3].

D. Sparks, “Student perceptions of college—how to move beyond transactional approaches to higher education,” Higher Education, vol. 85, pp. 477-481, Feb. 2022.

[4].

G. Sharma, M. A. Yukhymenko-Lescroart, and C. Scarton, “Purpose and career development: implications for career counseling and counselor education,” International Journal for Educational and Vocational Guidance, vol. 23, pp. 481-497, Sep. 2023.

[5].

J. F. Lu, C. Li, C. A. Potts, and J. Ufomadu, “An exploration of variables that contribute to counseling students’ spiritual competence development: implications for counselor education,” International Journal for the Advancement of Counselling, vol. 42, pp. 200-216, Nov. 2020.

[6].

K. Y. Fan, J. C. Carey, E. Thomas, C. Griffith, C. Wells, L. J. He, and J. Niu, “Development and exploratory factor analysis of a United States’ version of the international survey of school counselors’ activities,” International Journal for the Advancement of Counselling, vol. 41, no. 2, pp. 339-360, Jun. 2019.

[7].

Z. Wang, K. Liu, J. Li, Y. Zhu, and Y. Zhang, “Various frameworks and libraries of machine learning and deep learning: a survey,” Archives of Computational Methods in Engineering, vol. 26, no. 3, 2019.

[8].

A. E. Ezugwu, A. K. Shukla, M. B. Agbaje, O. N. Oyelade, A. Jose-Gacia, and J. O. Agushaka, “Automatic clustering algorithms: A systematic review and bibliometric analysis of relevant literature,” Neural Computing and Applications, vol. 33, pp. 6247-6306, Aug. 2021.

[9].

N. Shahid, “Comparison of hierarchical clustering and neural network clustering: an analysis on precision dominance,” Scientific Reports, vol. 13, no. 1, pp. 5661, Mar. 2023.

[10].

Y. Liu, T. Hou, Y. Miao, and F. Liu, “IM-c-means: A new clustering algorithm for clusters with skewed distributions,” Pattern Analysis and Applications, vol. 24, no. 3, pp. 1-13, Aug. 2021.

[11].

M. Tsunoda, A. Monden, K. Matsumoto, S. Ohiwa, and T. Oshino, “Analysis of work efficiency and quality of software maintenance using cross-company dataset,” IEICE Transactions on Information and Systems, vol. E104.D, no. 1, pp. 76-90, Jan. 2021.

[12].

S. H. Wu, A. H. Pitafi, S. Pitafi, and M. L. Ren, “Investigating the consequences of the socio-instrumental use of enterprise social media on employee work efficiency: A work-stress environment,” Frontiers in Psychology, vol. 12, p. 738118, Mar. 2021.

[13].

X. P. Yang, H. Ye, and X. W. Wang, “Social media use and work efficiency: insights from the theory of communication visibility,” Information & Management, vol. 58, no. 2, pp. 103462, Mar. 2021.

[14].

Z. Fang, Y. H. Chiu, T. Y. Lin, and T. H. Chang, “Economic, social, medical, work injury, and environmental efficiency assessments,” Inquiry-The Journal of Health Care Organization Provision and Financing, vol. 57, Feb. 2020.

[15].

N. K. Krivulin and S. A. Gubanov, “Algebraic solution of a problem of optimal project scheduling in project management,” Vestnik St. Petersburg University, Mathematics, vol. 54, pp. 58-68, Jan. 2021.

[16].

M. Navinchandran, M. E. Sharp, M. P. Brundage, and T. B. Sexton, “Discovering critical KPI factors from natural language in maintenance work orders,” Journal of Intelligent Manufacturing, vol. 33, no. 1, pp. 1859-1877, Jan. 2022.

[17].

A. M. Toda, A. C. T. Klock, W. Oliveira, P. T. Palomino, L. Rodrigues, L. Shi, I. Bittencourt, I. Gasparini, S. Isotani, and A. I. Cristea, “Analysing gamification elements in educational environments using an existing gamification taxonomy,” Smart Learning Environments, vol. 6, pp. 16, May 2019.

[18].

T. Wang, D. Wang, and Z. Liu, “Feedback-seeking from team members increases employee creativity: the roles of thriving at work and mindfulness,” Asia Pacific Journal of Management, vol. 39, pp. 1321-1340, Sep. 2022.

[19].

K. F. Kowalewski, C. R. Garrow, M. W. Schmidt, L. Benner, B. P. Muller, and F. Nickel, “Sensor-based machine learning for workflow detection and as key to detect expert level in laparoscopic suturing and knot-tying,” Surgical Endoscopy, vol. 33, no. 1, pp. 3732-3740, Nov. 2019.

[20].

H. T. El-Kassabi, M. A. Serhani, M. M. Masud, K. Shuaib, and K. Khalil, “Deep learning approach to security enforcement in cloud workflow orchestration,” Journal of Cloud Computing, vol. 12, no. 1, pp. 10, Jan. 2023.

[21].

L. Leng, M. Li, C. Kim, and X. Bi, “Dual-source discrimination power analysis for multi-instance contactless palmprint recognition,” Multimedia Tools and Applications, vol. 76, no. 1, pp. 333-354, Jan. 2017.

[22].

L. Leng and J. C. Zhang, “Palmhash code vs. PalmPhasor code,” Neurocomputing, vol. 108, pp. 1-12, Oct. 2013.

[23].

X. X. Lei, H. L. Ouyang, and L. J. Xu, “Kernel-distance-based intuitionistic fuzzy c-means clustering algorithm and its application,” Pattern Recognition and Image Analysis, vol. 29, no. 4, pp. 592-597, Oct. 2019.

[24].

A. V. Eremeev, A. V. Kel’manov, M. Y. Kovalyov, and A. V. Pyatkin, “Selecting a subset of diverse points based on the squared euclidean distance,” Annals of Mathematics and Artificial Intelligence, vol. 90, pp. 965-977, Feb. 2022.

[25].

G. C. Cardarilli, L. D. Nunzio, R. Fazzolari, A. Nannarelli, M. Re, and S. Spano, “N-dimensional approximation of euclidean distance,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, pp. 565-569, Apr. 2020.

[26].

A. Martino, A. Ghiglietti, F. Ieva, and A. M. Paganoni, “A k-means procedure based on a Mahalanobis type distance for clustering multivariate functional data,” Journal of the Italian Statistical Society, vol. 28, no. 2, pp. 301-322, Jun. 2019.

[27].

M. M. NezhadShokouhi, M. A. Majidi, and A. Rasoolzadegan, “Software defect prediction using over-sampling and feature extraction based on Mahalanobis distance,” The Journal of Supercomputing, vol. 76, pp. 602-635, Feb. 2020.

[28].

S. C. Zhang, Y. H. Wang, J. F. Li, P. Wan, Y. W. Zhang, and N. Li, “A cooperative spectrum sensing method based on information geometry and fuzzy c-means clustering algorithm,” EURASIP Journal on Wireless Communications and Networking, vol. 2019, pp. 17, Nov. 2019.

[29].

Y. F. Ke, “Convergence analysis on matrix splitting iteration algorithm for semidefinite linear complementarity problems,” Numerical Algorithms, vol. 86, pp. 257-279, Jan. 2021.

[30].

G. S. Narayana, “Fuzzy K-means clustering with fast density peak clustering on multivariate kernel estimator with evolutionary multimodal optimization clusters on a large dataset,” Multimedia Tools and Applications, vol. 80, no. 3, pp. 4769-4787, Aug. 2021.

[31].

O. Şeref, Y. J. Fan, E. Borenstein, and W. A. Chaovalitwongse, “Information-theoretic feature selection with discrete k-median clustering,” Annals of Operations Research, vol. 263, no. 1, pp. 93-118, May 2018.

[32].

D. Huang, C. D. Wang, H. X. Peng, J. H. Lai, and C. K. Kowh, “Enhanced ensemble clustering via fast propagation of cluster-wise similarities,” IEEE Transactions on Systems Man Cybernetics-Systems, vol. 51, pp. 508-520, Jan. 2021.

[33].

K. P. Sinaga and M. S. Yang, “Unsupervised K-means clustering algorithm,” IEEE Access, vol. 8, pp. 80716-80727, Mar. 2020.

AUTHOR

jmis-10-4-351-i1

Yuzhou Ke was born in Shangrao, Jiangxi. P.R.China, in 1984. She received the Master degree from Nanchang University, P.R. China. She is currently working in Business Administration College of Guangdong Baiyun University. Her research interests include ideological and political education, innovative work programs, etc.