I. INTRODUCTION
Chaos is a phenomenon very close to randomness, which occupies an important position in cryptography, but determinism and dynamics distinguish it from randomness. In the past three decades, chaos has swept through most sciences (mathematics, physics, biology). It is defined by a nonlinear equation that is very sensitive to initial conditions. The expansion of chaos theory is closely related to the development of computer science and new mathematical advances (modeling, simulation, etc.). Like all new theories, chaos theory is still the subject of many controversies. Various forms of disputes have caused disputes over legal opinions and interpretations. Will science be able to explain it more and more, or is it impossible to understand the world by accident? In fact, for scientists, this is a matter of defining the complexity of the phenomenon they are studying. Chaos as understood by scientists does not mean that there is no order. In fact, this is related to unpredictability, because the final state is very sensitive to the initial state, so long-term evolution cannot be predicted. We believe that the difference between chaos and randomness is the most important point for understanding chaos. Indeed, there is always a tendency to believe that a phenomenon is unpredictable due to the large number of parameters involved. In his description, this prompted us to give a probabilistic method, which by definition can satisfy a certain degree of freedom completely satisfactorily. Randomness. As far as chaos is concerned, this is actually not the case, and the behavior of the chaotic system seems to be random. But in reality, this behavior is described in a deterministic way by fully deterministic nonlinear equations, that is, in particular using mathematics that allow accurate and deterministic methods. To explain with a famous advertisement, a person can write: “Looks like an opportunity, tastes like an opportunity, but not accidental. With the passage of time, people have made several attempts to build a chaotic graph and realized the password. The large number of chaotic graphs used in learning [1]. Other technologies use chaotic maps to construct hash functions [2]. On the other hand, other technologies use chaotic cards in symmetric encryption systems [3]. There are also some the technology combines several chaotic maps to improve performance. Their systems [4],[5],[6] were in the absence of any deterministic formula for generating random numbers, tables of such numbers appeared.
Abreviation
Finding that they were unable to master random numbers, researchers quickly turned to the generation of pseudo-random numbers defined by mathematical relationships that produce the same sequence under the same conditions. Among all these technologies, we mentioned the most important ones.
In 1946 Von Neumann proposed the following pseudo-random number generator
The linear congruential generator was introduced by Lehmer, and is still popular in today’s methods for generating pseudorandom numbers quickly. The sequence of random numbers (xn) is created as follows:
Linear congruence generator
In order to be able to choose a seed x0 without constraints between 0 andn − 1, it is necessary to try to maximize the generator period. However, it turns out that the values of a and c are known, which makes it possible to obtain a maximum period (equal to n). the period of a linear congruential generator is maximum if and only if:
Functions that generate chaotic sequences can be divided into two categories: one-dimensional sequences and multi-dimensional sequences. Chaotic functions are rare in the literature, and there are only a dozen functions used in cryptography.
Logistic recursion [7] is a simple example of nonlinear sequence. It is defined by a simple relation managed by a second order polynomial described by the following recurrence relation.
Logistic recurrence
The Skew tent map [8] will be redefined as the equation below
The skew tent map
It is a real linear sequence [9] by pieces defined by the equation below
PWLCM
The simplicity and robustness of this card encourages researchers to use it in cryptography.
II. RECOMMENDED KNOWLEDGE
Before revealing the structure of this new map, it is necessary to define some basic properties. Let (f) be a continuous function over the interval(I) and defined by the equation.
continuous function
We are going to give some definitions to clarify all the points of the article.
Let (x) be an element of (I), we call the trajectory of x the set of iterates of (x) by the function (f). This set is defined by
Trajectory
We say that x ∈ I is periodic if there is an integer (r) such that
Periodicity
In that case we’ll have
The (l) period of an element x ∈ I is the smallest integer r such that
Period
We notice that if (l) is the period of element (x) then
Let (f) be a continuous function on I. We say that (f) is topologically transitive if:
Transitive topology
It is said that (f) is sensible to the initial conditions if
Initial condition sensitivity
In other words,
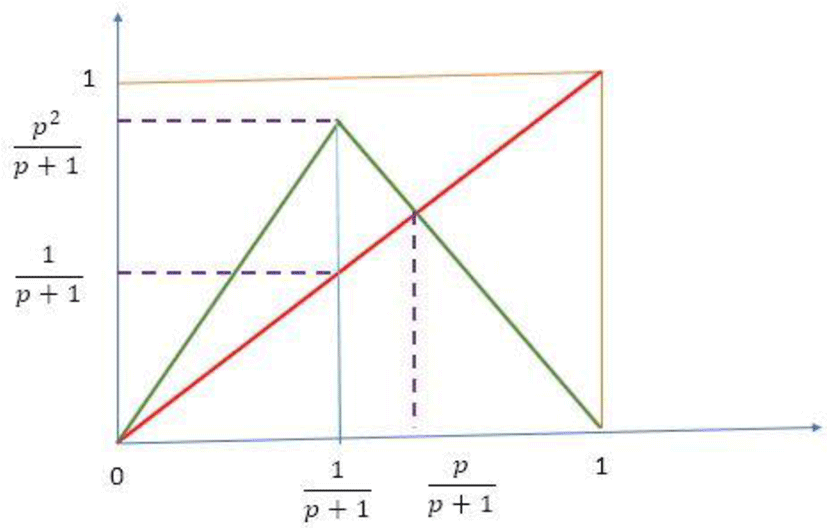
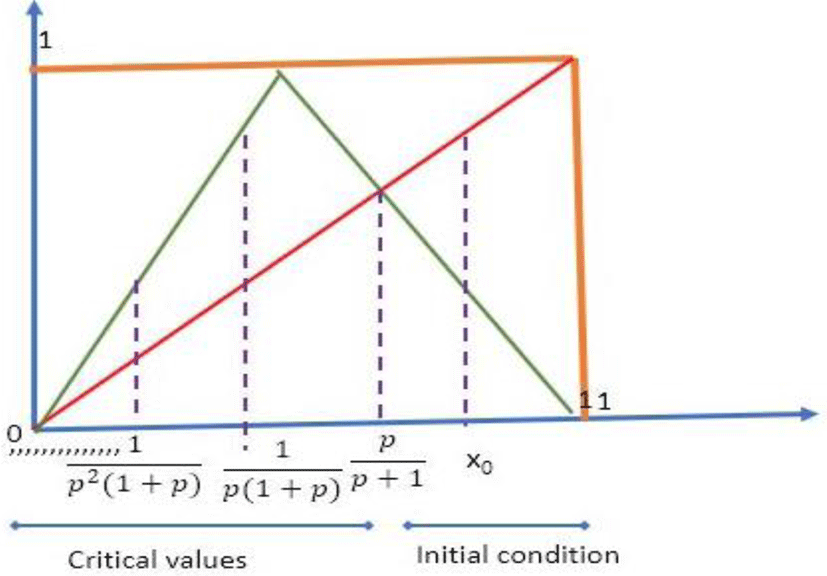
III. NEW CHAOTIC FUNCTION DESIGN
The function (f) defined by the equation can be represented by the following figure
For the sequence (xn) to exist it is necessary that f(I)⊂I. So, it is necessary that
Existence domain
The function (f) is continuously derivable and its derivative is given by the expression
Derived from f
The sequence (xn) is defined by the following expression
Chaotic sequence building
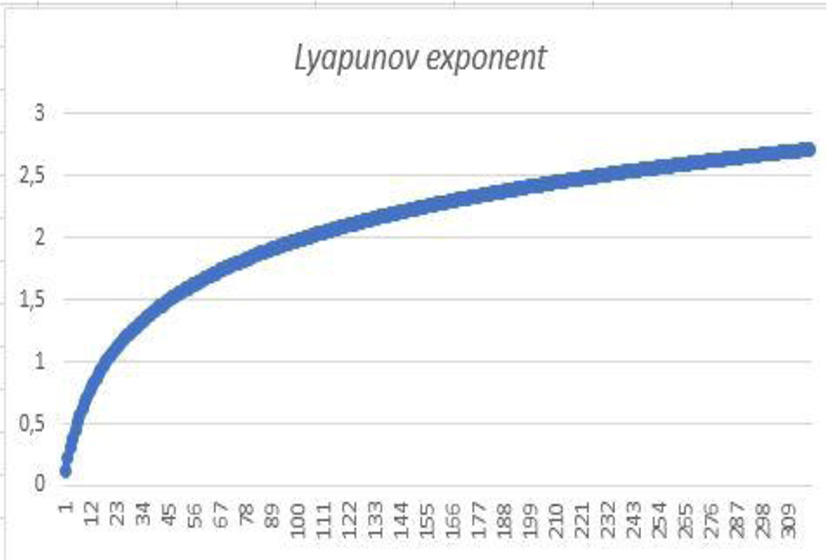
To measure the sensitivity to the initial conditions of the sequence (xn) defined by function (f) , we have to calculate the Lyapunov exponent
Lyapunov exponent
In our case, we notice that
We can conclude from the value of the Lyapunov exponent that the sequence (xn) defined by the function (f) is sensitive to the initial conditions. This value is higher than the value of the logistics diagram, indicating that it is highly sensitive to initial conditions and control parameters.
The logarithmic scale plot shows that the distance between two very close initial conditions varies according to an exponential law.
Order of Sarkovkii
Sarkovskii’s Theorem
All-natural integers are represented in this Sarkovkii order.
The first line represents odd numbers
The row line (n) represents the numbers 2n−1 (2k+1)
Let f: I → I continue. Suppose that (f ) has a periodic point of period ( k). If (k ≻ ℓ) according to Sarkovskii’s order, then f also has a periodic point of period (ℓ).
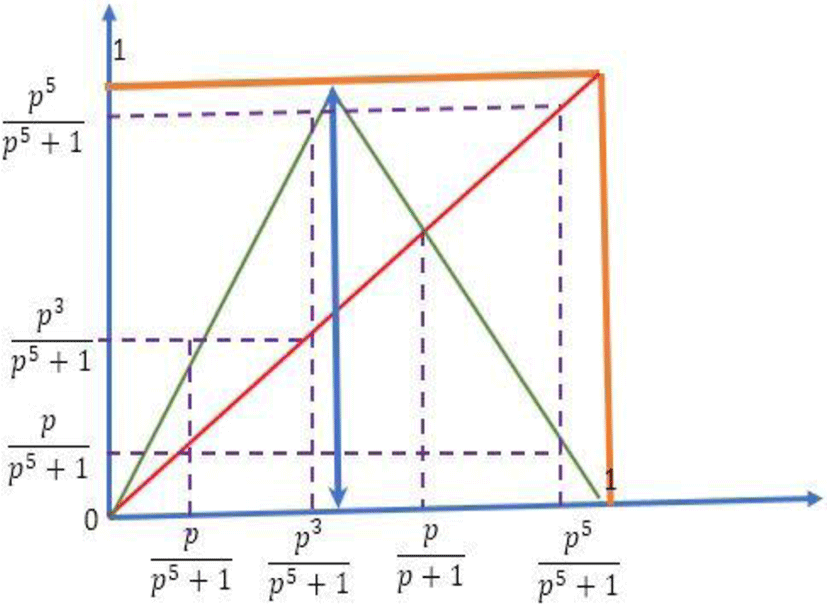
If (f) admits an item from period 3, then it admits an item of any order. As a result, the function has a chaotic appearance.
Search for
Let
Period point 3
Let’s demonstrate that (x⋆) is a point of period 3
Let’s prove that
Let’s put
Therefore
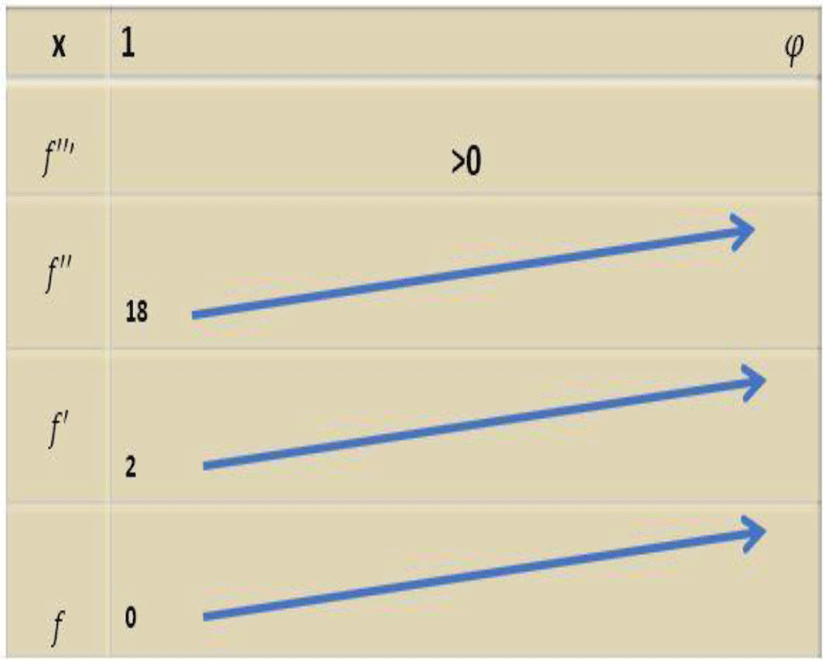
The following table gives the variations of the functions
So
Therefore:
Let’s look at the sign of the function (f) defined by
According to a rough calculation we have
Forp ∈ [1,47 φ] f′p) > 0
is a periodic point of period 3, therefore (f ) is a chaotic function according to Sarkovskii’s corollary. This period point 3 is illustrated by the following figure
We know that the only fixed points are
Period doubling
searches for points (x0) for which there is a k such that
If there is such a point (xn) then the sequence (xn) is stationary.
For (k=1), we have
For (k = 2), we have
By recurrence, we obtain
For (k = n), we have
If there is (n) such that the initial condition , then the sequence would be stationary from the n iteration onwards. Then the sequence is no longer chaotic.
We construct a sequence (yn) defined by:
(yn) is a decreasing sequence minus 0, converging donations, and we have the following equation;
Finally
This is illustrated by the following curve
The sequence (xn) defines is a chaotic sequence under the specified conditions.
We are looking for an element such as
If such a point exists then two situations present themselves
Situation 1
Situation 2
So
In this case the sequence would be stationary from iteration (k)
Moreover, we have,
Finally
This sequence is chaotic.
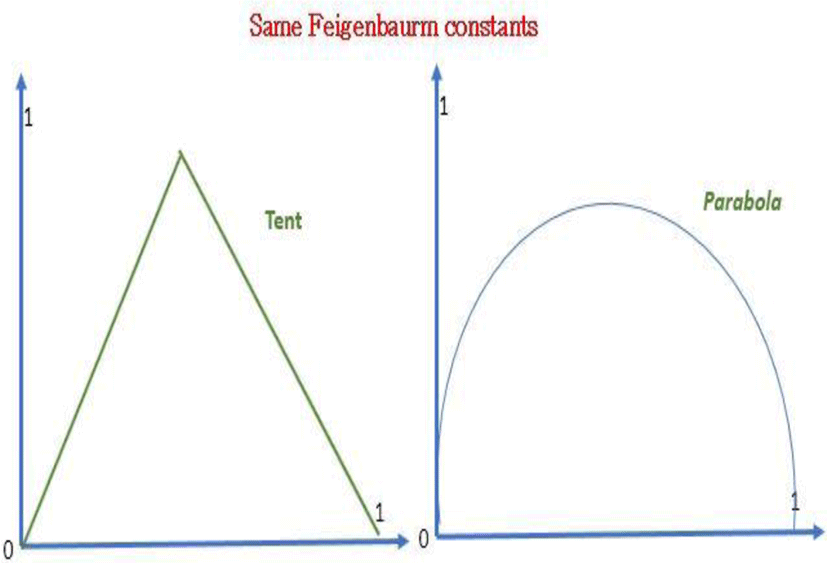
In 1975 the physicist Feigenbaum noticed that the general pattern of the logistic sequence was repeated at each bifurcation to within a factor of scale. He then used a process of renormalization. This involves enlarging smaller and smaller parts of the graph and comparing these magnifications to the original pattern. When the enlarged pattern reproduces the first pattern, it is called self-simulation. As it grows to infinity, the general structure repeats itself. If globally, the duplications are not the same, they keep the same ratios
The first constant intervening horizontally
The second constant occurring vertically
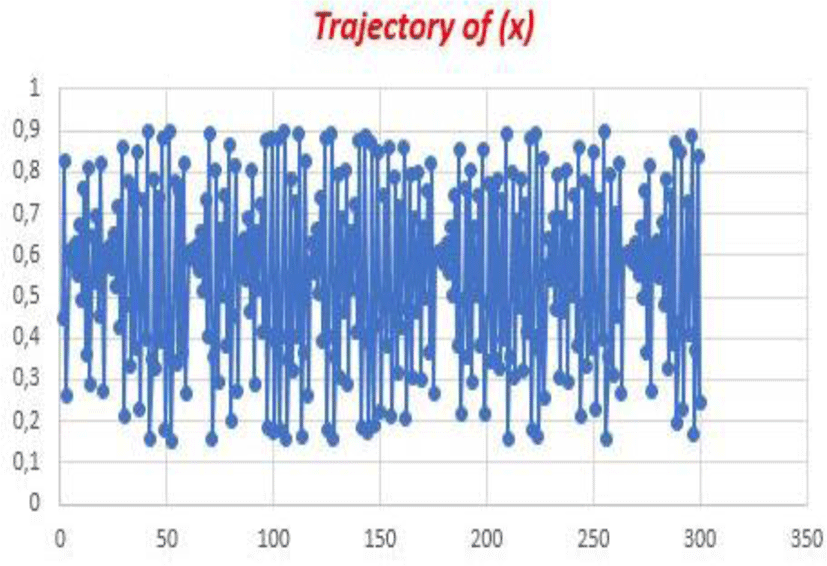
The trajectory seems to be random
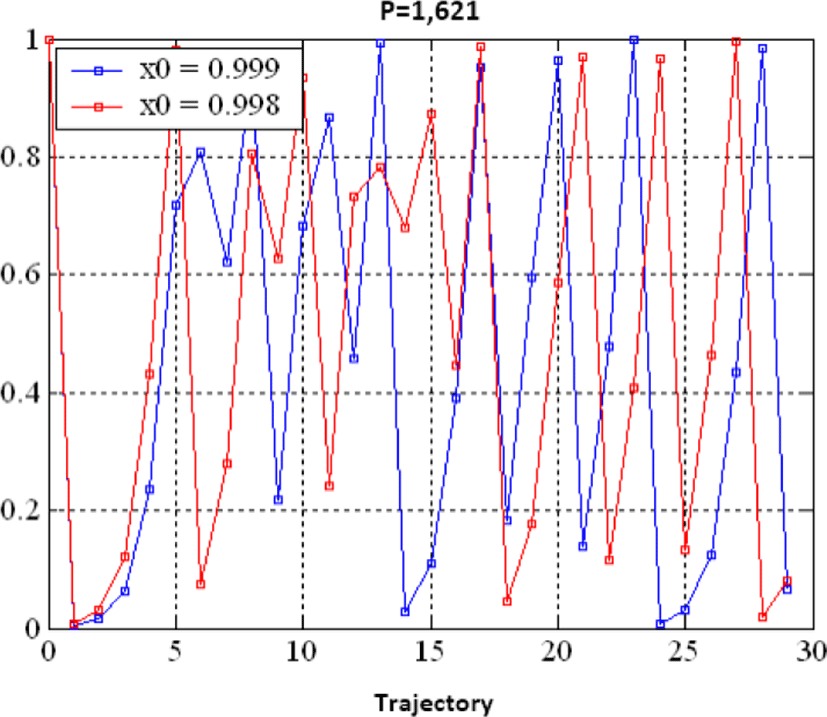
For two very close values of the initial conditions attached to the same control parameter (p) we see the deviation of the trajectories, this is due to the strong sensitivity to the initial conditions provided by the value of the Lyapunov exponent.
We have noticed that small disturbances under initial conditions will greatly deviate from the trajectory.
The sensitivity to initial conditions of a chaotic map measures its robustness against abrupt attacks. Our map is one-dimensional, a comparison with the most used maps is given by the following table.
| Chaotic map | Lyapunov exponent |
|---|---|
| Logistic Map | Ln (2) |
| PWLCM | Ln (2) |
| Tent Map | Ln (2) |
| Our Map | 3/2Ln(p)>>Ln(2) |
IV. CRYPTOGRAPHY APPLICATION
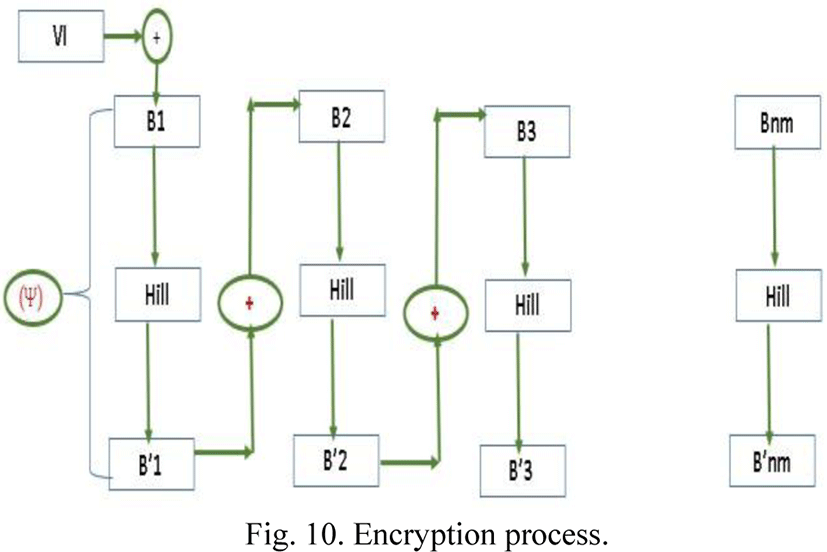
We will introduce the improvement of Hill’s classic method using the new chaotic map as the private key to illustrate the performance of our new chaotic map. After reading the original image and switching to the vector, a chaotic vector of the same size is generated from the new map (in the simulation, we take p = 1.54, x0 = 0.623).
-
Subdivision of the image vector into blocks of three pixels, as well as the chaotic vector.
-
Calculation of the initialization vector
-
Modification of the priming block
-
Application of Hill’s improved method.
-
Application of dissemination
-
Reconstruction of the encrypted image
-
The encryption process is as follows
The encryption function is defined by
Encryption process
The use of vector (Tvi) aims to overcome the linearity problem of classical systems.
Construct the encryption key matrix from the new chaotic map by the following expression.
After the simulation is complete, we get
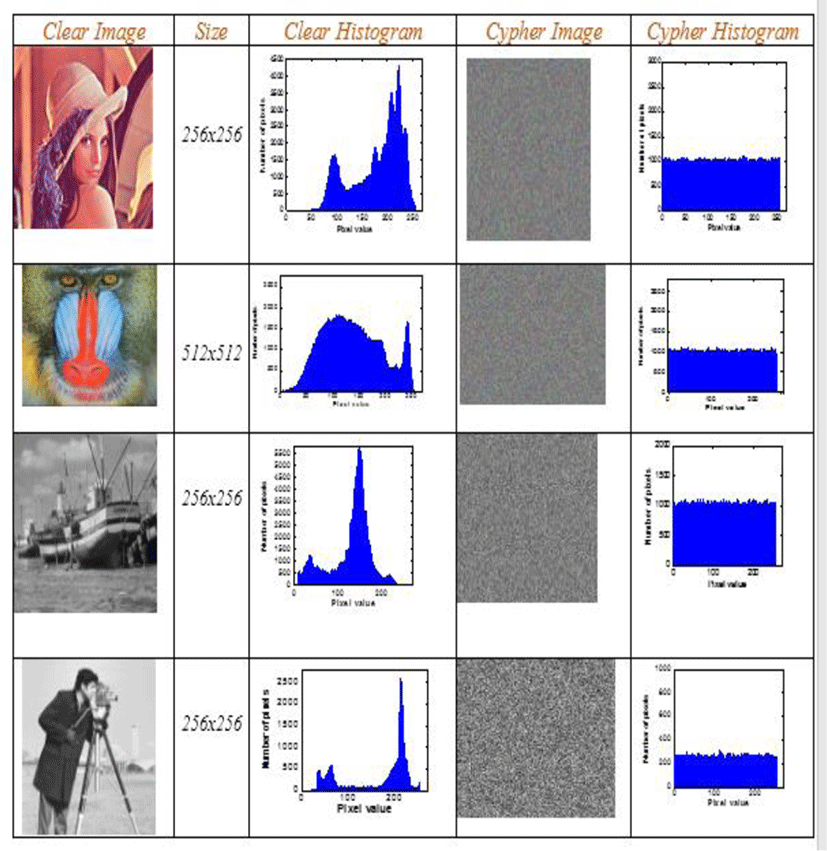
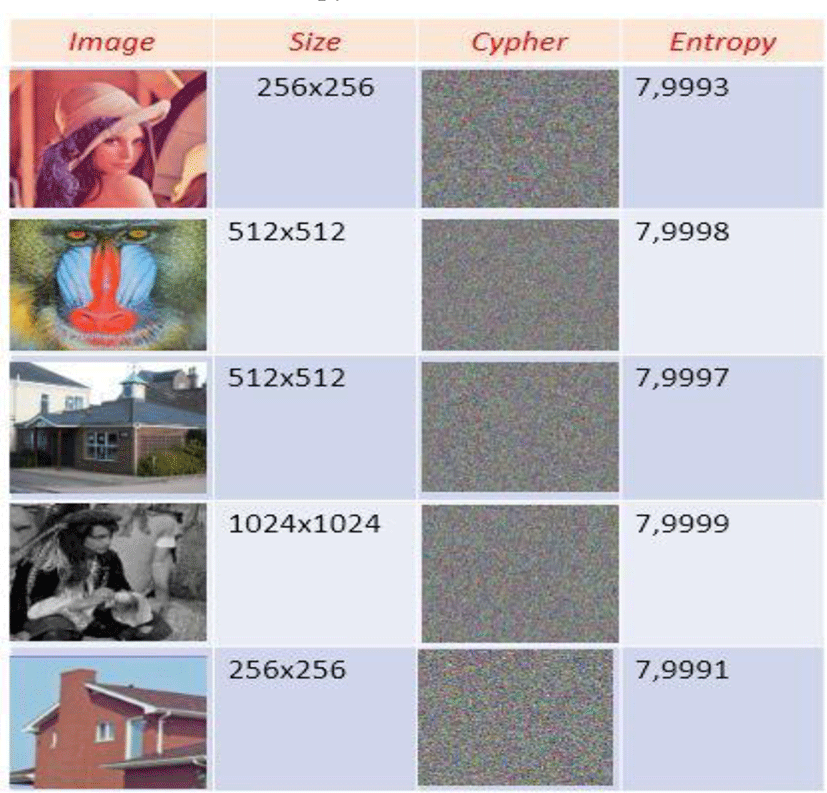
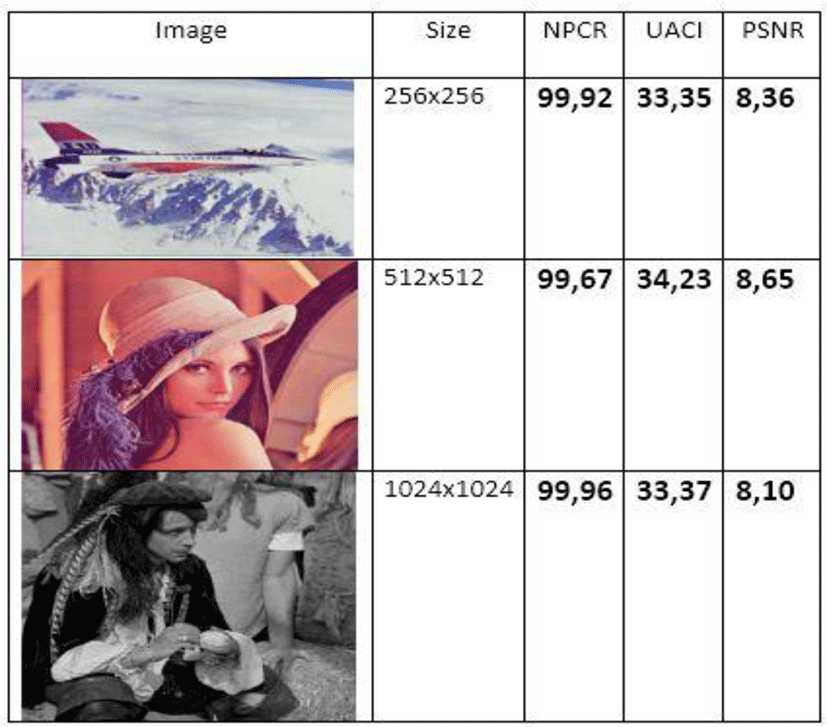
All images tested by our algorithm generate encrypted images with uniform and flattened histograms of pixel distribution. These histograms give an entropy value very close to the maximum value (8). This ensures a strong protection of our new technology against any entropy attack. The calculation of the entropy value is given by the table below
The use of the encryption mode provides strong protection for our system against differential attacks. The table below illustrates the different values of the differential statistical constants.
Our algorithm uses a strong link between encrypted pixels and pixels with clear policies. As a result, as data propagates through the structure of the algorithm, gradual changes become increasingly important. The avalanche effect is the number of bits that have been changed if a single bit in the original image is changed. The mathematical expression of this avalanche effect is given by
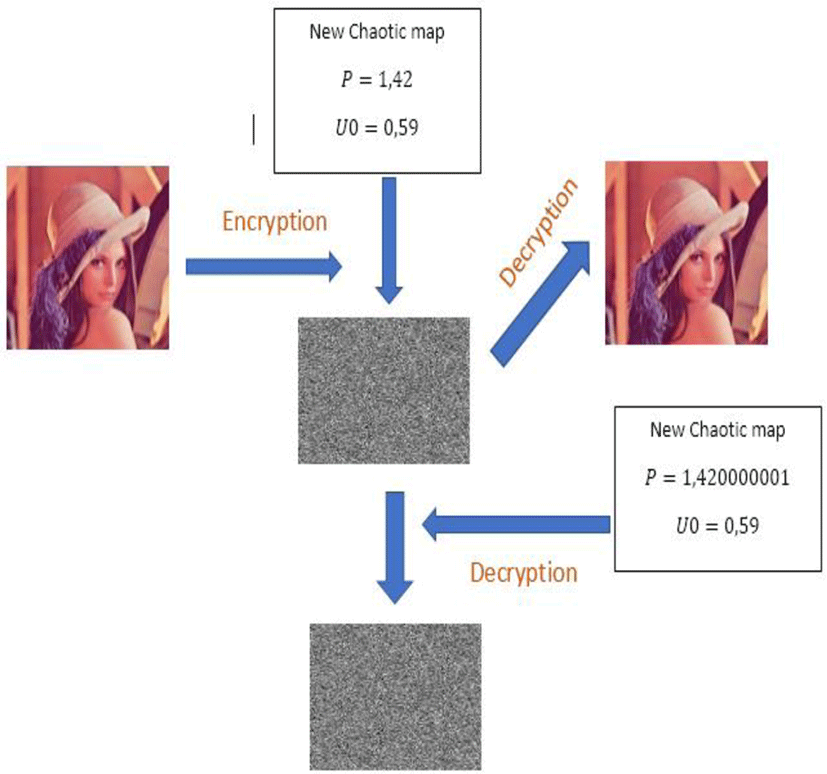
The high sensitivity of our new chaotic map makes our algorithm immune to brute force attacks. This sensitivity is illustrated by the following figure
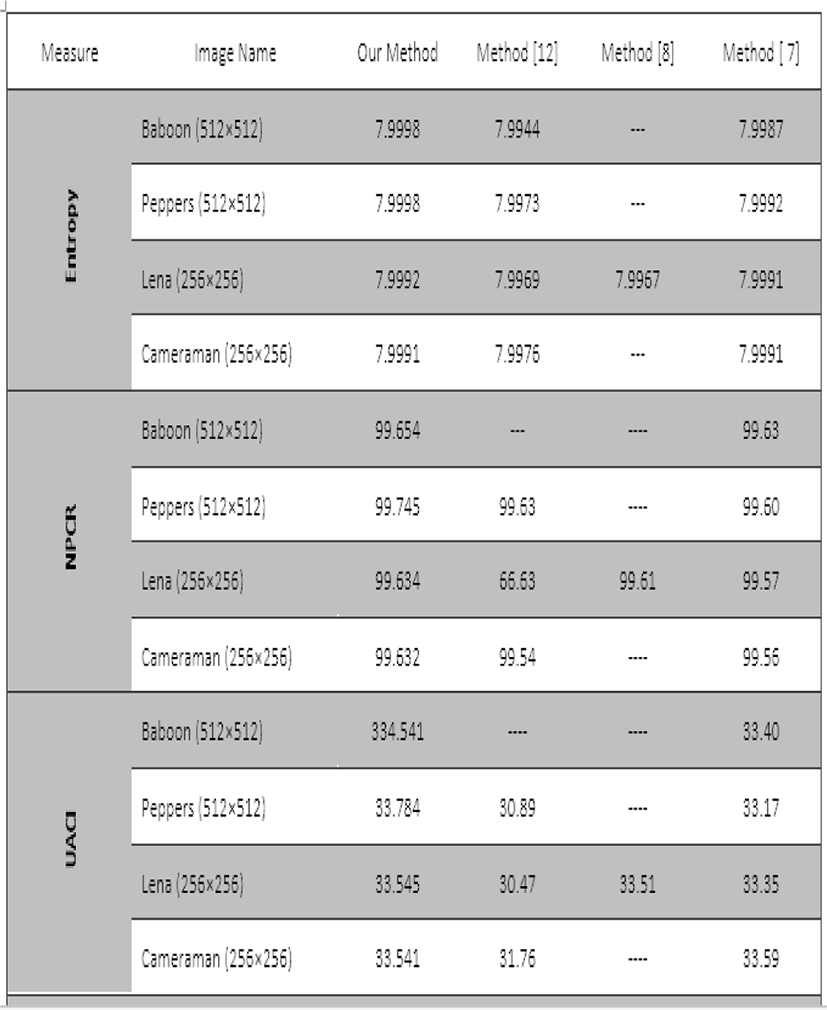
A rapid comparison between our example using a chaotic map with an enhanced Vigenere and other techniques. This minimal comparison, illustrated in the following table, highlights the complexity of our system, devoted by the new chaotic map.
V. CONCLUSION
Faced with various difficulties in constructing random numbers, researchers are committed to using generators that follow simple mathematical formulas to create pseudo-random numbers. With the passage of time, chaos theory suddenly appeared, and due to the need to use passwords with such numbers to create private encryption attack. Using logarithms and discrete exponents and translation vectors to overcome linear problems will increase the complexity of our method.