Brief Paper: An Approach to Improve the Contrast of Multi Scale Fusion Methods

Hwang, Tae Hun; Kim, Jin Heon

doi:10.9717/JMIS.2018.5.2.87

J Multimed Inf Syst 5(2):87-90

eISSN: 2383-7632

DOI: https://doi.org/10.9717/JMIS.2018.5.2.87

Section A

Brief Paper: An Approach to Improve the Contrast of Multi Scale Fusion Methods

Tae Hun Hwang¹^,^*, Jin Heon Kim²

Author Information & Copyright ▼

¹Dept. of Computer Eng., Seokyeong University, Seoul, Korea

²Dept. of Computer Eng., Seokyeong University, Seoul, Korea, jinheon@skuniv.ac.kr

^*Corresponding Author: Tae Hun Hwang, Bukakkwan 513, Seokyeong-ro 124, Seong buk-gu, Seoul, Korea, 02713, +82-2-640-7747, xognsdl82@gmail.com

© Copyright 2018 Korea Multimedia Society. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Mar 10, 2018 ; Revised: May 10, 2018 ; Accepted: May 15, 2018

Published Online: Jun 30, 2018

Abstract

Various approaches have been proposed to convert low dynamic range (LDR) to high dynamic range (HDR). Of these approaches, the Multi Scale Fusion (MSF) algorithm based on Laplacian pyramid decomposition is used in many applications and demonstrates its usefulness. However, the pyramid fusion technique has no means for controlling the luminance component because the total number of pixels decreases as the pyramid rises to the upper layer. In this paper, we extract the reflection light of the image based on the Retinex theory and generate the weight map by adjusting the reflection component. This weighting map is applied to achieve an MSF-like effect during image fusion and provides an opportunity to control the brightness components. Experimental results show that the proposed method maintains the total number of pixels and exhibits similar effects to the conventional method.

Keywords: Retinex Theory; Multi Scale Fusion; Weight Map

I. INTRODUCTION

Due to the limitation of the camera’s dynamic range, we cannot acquire dark and bright area information at the same time. This problem can be solved by shooting several times with different exposure values. There has been widely discussed that methods of combining various images with different exposures into a single HDR image [1-6].

One of these is the Laplacian pyramid decomposition and is useful in many applications. However, image fusion based on the image pyramid method has a smaller image size as the number of pyramid layer increases. Decreasing the total number of pixels in the image reduces the way you can control the brightness of the pixels. When you reach the topmost layer of the pyramid, you cannot control the brightness component. In other words, the overall brightness of the image can be highly dependent on the brightness of the pixels around each area.

As a result, unwanted areas become lighter or darker. In this paper, we propose a method of extracting reflection components from images and applying them to image fusion based on Retinex theory [7] which has the same effect as existing MSF algorithm and does not reduce image size.

II. FORMULATION OF THE PROBLEM

2.1. Multi Exposure Image Fusion

2.1.1. Multi-Scale Image Fusion

A fusion of Laplacian pyramid decomposition produces a weight map through some intuitive measure the exposure of different images. The generated weight map and images with different exposure are appropriately mixed to create a single image. The formula of the image fusion using the generated weight map is as follows:

R = ∑ ​ m = 1 M ∑ ​ n = 0 N − 1 [{G n {w (m)} * L n {I (m)}} + G N {w (m)} * G N {I (m)}]

(1)

In equation (1), parameter M represents the number of multi-exposure images with different exposure and N represents the number of layers of the image pyramid

2.1.2. Single-Scale Image Fusion

The MSF method determines the number of layers in the image pyramid based on the image size, so it takes a lot of time. In [6], the computation is simplified by approximating the MSF equation. The simplified formula is as follows:

R SSF = ∑ n = 1 N [G N {w (n)} + α * L 1 {I (n)}] * I (n)

(2)

In equation (2), the detail of the Laplacian image is reflected in the weight map by the edge emphasis α value.

2.2. Retinex Theory

2.2.1. Single Scale Retinex

Retinex theory of human visual effects is compound of retina and cortex. When the human eye detects an object, it is affected by the surrounding light as well as the reflection of the object. At this time, the human eye has an action to remove the illumination component. This is Retinex theory. This can be expressed as follows.

I i (x, y) = R i (x, y) * L i (x, y)

(3)

Parameter I mean the finally obtained image, and R and L mean the illumination component and the reflection component, respectively.

2.2.2 Multi Scale Reitnex

The MSR is an algorithm that complements the disadvantages of the SSR algorithm. The MSR estimates the illumination with multiple illumination estimation functions. SSR cannot improve enough contrast depending on the characteristics of the image [9]. The MSR algorithm solves the SSR problem by adding weights to the various lighting estimation functions.

M S R (x, y) = ∑ ​ n = 1 N W n R n (x, y), ∑ ​ n = 1 N W n = 1

(4)

In the above equation (4), n denotes the number of illumination estimation functions of different sizes.

III. PROPOSED METHOD

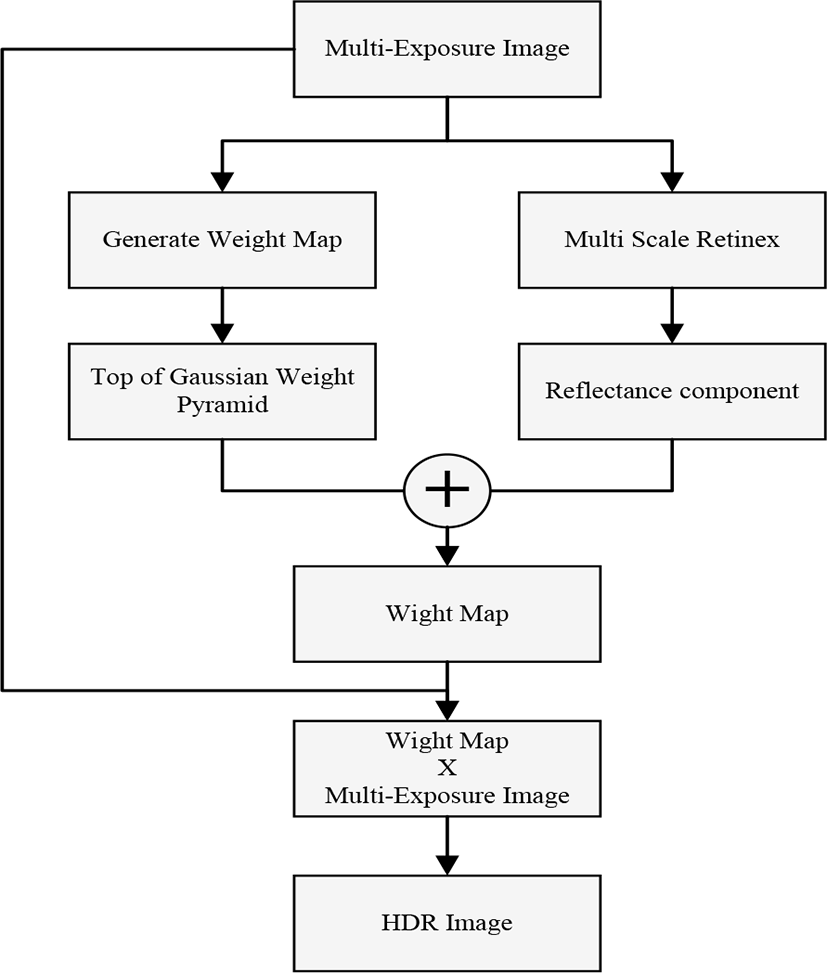
The traditional MSF algorithm uses a weight map to generate a Gaussian pyramid for image fusion. As the pyramid layer increases, the image size decreases. The higher the layer, the greater the effect of the surrounding area on the pixel intensity. That is, certain unwanted areas can be darkened by the surrounding area, and vice versa. Therefore, in this paper, we propose a method to maintain the image size with similar effect to the existing MSF method. Figure 1 shows the processing flow of the proposed method. We use the input image to obtain the weight map and the reflection component. Creates a new weight map by summing the weight and reflective elements. This applies to multiple exposure images to fuse HDR images.

Fig. 1. Flowchart of the proposed method

Download Original Figure

3.1. Separation of Light and Reflectance

The way of obtaining the reflection component and the illumination component in the image can be obtained by using the formula (5) which is the basis of the Retinex theory.

R i (x, y) = I i (x, y) L i (x, y)

(5)

Weber-Fechner, and there is a log relationship between what is actually applies law [8] exists in the human visual perception system and the sensation sensed by humans. Based on this, equation (5) can be transformed into the (6).

R ` i (x, y) = log (I i (x, y) L i (x, y))

(6)

As shown in equation (6), it estimates the illumination component of the surrounding area to obtain the reflection. In this paper, we use a Gaussian filter to estimate the illumination. We used a total of three Gaussian filters to evaluate multiple lights. Weber-Fechner's law was used to combine three reflective components into one image. This rule means that changes in low-light areas are more sensitive than changes in high-brightness areas. In other words, the image quality is better as a result of emphasizing contrast in low light areas. The expression for extracting low-light areas from an image is:

W low, k = exp (− 0.5 * (I k − 0.3) 2 2 σ 2)

(7)

The low-light areas of the image obtained in equation (6) are combined into one image as shown below.

R l o w = ∑ ​ n = 1 N W l o w, n * R n ` (x, y), ∑ ​ n = 1 N W l o w, n = 1

(8)

3.2. Generation Weight Map

3.2.1. Visual Evaluation Index

Various methods of generating a weight map are discussed [5], [6], [10]. In this paper, we have used three contrast, saturation and well-exposed indicators proposed by Merten et al. [5] was used to extract the preferred pixels from multiple exposure images. Based on this, it creates the top Layer of Gaussian pyramid.

3.2.2. Top Layer of Gaussian Weight Pyramid

This paper simplifies the Gaussian pyramid generation process. For Gaussian filtering, the sigma value is proportional to the number of pyramid layer. This filter has the same effect as the top layer of Gaussian pyramid. The formula for deriving the sigma value by calculating the number of pyramid layers is as follows:

level = log (min (r o w I, c o l I)) log (2)

(9)

Sigma = 2 level − 1

(10)

Using large sigma values in Gaussian filtering requires a lot of computation time. Thus, the calculation is performed in the frequency domain when performing filtering.

3.3. Multi-Exposure Image Fusion

A new weight map is generated by adding the obtained reflection component and the uppermost layer of the Gaussian pyramid, and the new weight map is multiplied by the original image to fuse a plurality of exposed images.

R SSF = ∑ n = 1 N [G {w (n)} + R l o w, n] * I (n)

(11)

IV. EXPERIMENTAL RESULTS

The results of the proposed method and the MSF method are compared with each other through an evaluation index. The images used in the experiment were two images with different impressions. Experimental results show that the proposed method has similar performance to MSF algorithm and it is confirmed by using SSIM and AMBE evaluation index. Comparing with the SSF algorithm [6], which approximates the MSF algorithm, we compare and analyze how similar the proposed algorithm is to the MSF results.

4.1. SSIM

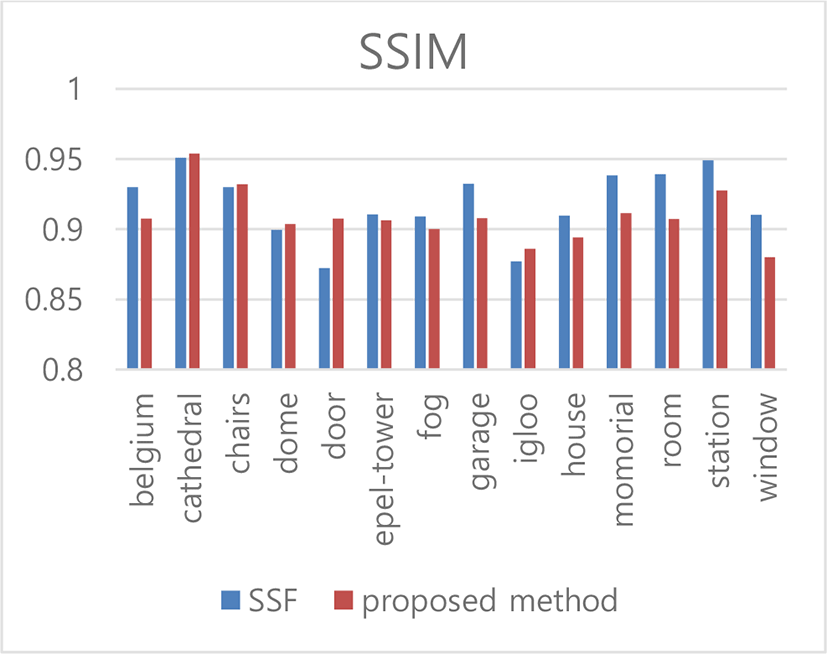
Structural Similarity Index (SSIM) represents the visual and structural similarity between the original image and the resulting image, and is composed of complex indicators based on contrast, structure and luminosity. SSIM has a value of 1 when it is the same as the original, and has a value close to 0 if it is not similar.

Figure 2 compares the results of the proposed method with the results of the existing method through SSIM. The SSIM average difference between the two algorithms was about 1%. This means that it is structurally very similar to the resulting image of the MSF algorithm.

Fig. 2. SSIM Indicator Results Comparison Graph

Download Original Figure

4.2. AMBE

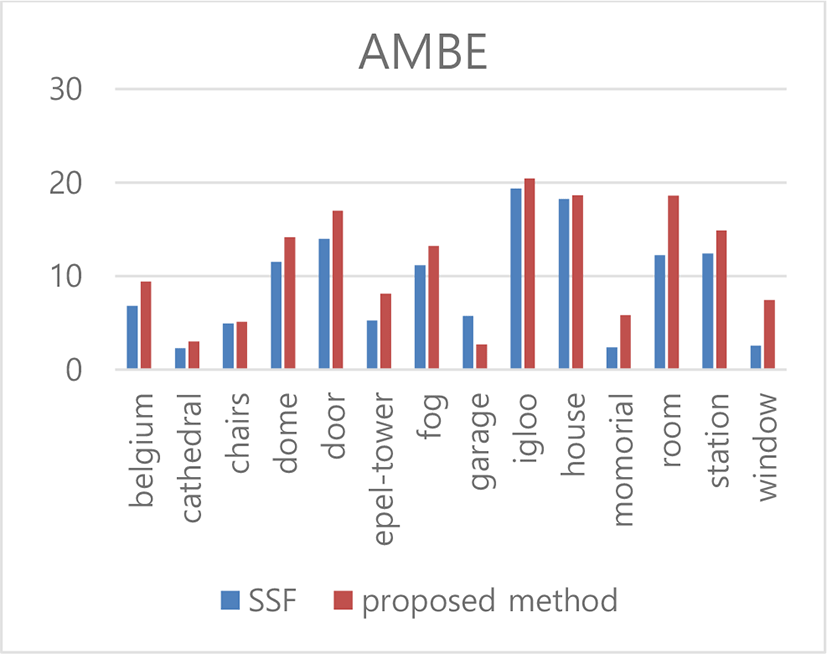
The AMBE (Absolute Mean Brightness Error) indicator measures the difference between the average brightness value of the resulting image and the average brightness value of the original image. This allows you to see how well the image contrast of the MSF algorithm is maintained.

AMBE (x, y) = | μ x − μ y |

(12)

If the brightness average of the image is small, the AMBE value is 0, and the larger the brightness difference, the larger the value.

Figure 3 compares the results of the proposed method with those of the existing method through AMBE. The AMBE mean difference between the two algorithms is about 0.8%. This means that the average brightness of the MSF algorithm is similar.

Fig. 3. SSIM Indicator Results Comparison Graph

Download Original Figure

V. CONCLUSION

In this paper, we propose a method to solve the brightness component control problem of the existing MSF algorithm by adding the reflection component of the image to the weight map generation. In the conventional MSF method, the brightness component of the image depends on the surrounding pixels because of the size of the reduced image in the process of generating the pyramid of the weight map. This means that depending on the characteristics of the image, the contrast ratio can be improved, but certain areas can become too dark or too dark. However, the proposed method has an effect similar to the existing MSF method by estimating the reflection component and fusing the image with a plurality of illumination functions, and has an opportunity to solve the MSF problem by maintaining the number of pixels of the image. The presently proposed method may result in bad images in some images because the size of the light evaluation function is a fixed value. This can be solved by setting the size of the illumination estimation function adaptively according to the characteristics of the image in future studies.

REFERENCES

[1].

F. Durand and J. Dorsey, “Fast bilateral filtering for the display of high-dynamic-range images”, journal of ACM Transactions on Graphics, vol. 21, no. 3, pp. 257-266, Jul. 2002.

[2].

J. M. DiCarlo and B. A. Wandell, “Rendering High Dynamic Range Images” Proceeding of the SPIE: Sensors and Camera Systems for Scientific, Industrial, and Digital Phtography Application, vol. 3965, May. 2000.

[3].

R. Fattal, D. Lischinski, and M. Werman, “Gradient Domain High Dynamic Range Compression”, Proceeding of the 29th annual conference on Computer graphics and interactive techniques SIGGRAPH `02, San Antonio, vol. 21, no 3, Jul. 2002.

[4].

P. E. Debevec and J. Malik, “Recovering High Dynamic Range Radiance Maps from Photographs”, Proceeding of the 24th annual conference on Computer graphics and Interactive techniques SIGGRAPH `97, Los Angeles, pp. 369-378, Aug. 1997.

[5].

T. Mertens, J. Kautz, and F. V. Reeth, “Exposure Fusion: A Simple and Practical Alternative to High Dynamic Range Photography” Journal of Computer Graphics forum, vol. 28, no. 1, pp. 161-171, Mar. 2009.

[6].

C. O. Ancuti, C. Ancuti, C. D. Vleechouwer and A. C. Bovik, “Single-Scale Fusion: An Effective Approach to Merging Images”, journal of IEEE Transactions on Image Processing, vol. 26, no. 1, Jan. 2017

[7].

D. H. Brainard and B. A. Wandell, “Analysis of the retinex theory of color vision”, journal of the Optical Society of America, vol. 3, no. 10, pp. 1651-1661, Oct. 1986.

[8].

F. W. Nutter Jr., P. D. Esker, “The role of psychophysics in phytopathology: The Weber-Fechner Law revisited”, European journal of Plant Pathology, vol. 114, no. 2, pp. 199-213, Feb. 2006.

[9].

J. Y. Kim and J. H. Kim, “Adaptive Unsharp Masking Filter Design Based on Multi-Scale Retinex for Image Enhancement”, journal of Korea Multimedia Society, vol. 21, No. 2, pp.108-116, Feb. 2018

[10].

S. J. Im and J. H. Kim, “A Pyramid Fusion Method of Two Differently Exposed Images Using Gray Pixel Values”, journal of Korea Multimedia Society, vol.19, No. 8, pp.1386-1394, Aug. 2016.