I. INTRODUCTION
Domestic meteorological observation network is more favorable than the observation density of USA or Japan when it comes to collecting and utilizing weather data as it is relatively dense. Precipitation observation facility has particularly high importance among other weather forecast equipment. Precipitation gauge observation facility has the measuring density (territory/precipitation gauge = 99,720 km2/642) of 155.3 km2 (based on a single ground rain gauge observation station) even when we only consider AWS (Auto Weather System ) which is operated by the national weather service and the observation density reaches 78.7 km2 (based on a single ground rain gauge observation station) if we sum up every ground precipitation gauge operated by the Ministry of Land (456 pcs) and the Water Resource Corporation (169 pcs) [1].
According to precipitation observation network, 70% of annual precipitation is usually concentrated in from the month of June to September which is a rainy season and this is caused by the geographical characteristics of our country in which typhoon enters from sea side to inland every year. However, dense ground hyetometer observation facility is not enough to deal with heavy rain that got into inland from the sea side due to increase in frequency of local concentrated heavy rain occurrence caused by climate change and extreme spatio-temporal variability in occurrence of precipitation. It is even more severe in the area where precipitation data is hardly collected at the initial state like a seaside.
Various studies are conducted to improve algorithm and method to estimate radar precipitations quantitatively in America and Japan, where radar is operated for the purpose of weather forecast, while radar equipment go through upgrade of radar equipment hardware. CASA (collaborative adaptive sensing of the atmosphere) project in America and TOMACS (Tokyo metropolitan area convection study for extreme weather resilient cities) in Japan are typical examples. First of all, CASA project proved applicability of new paradigm (DCAS) for detection of precipitation with overlapped observation range of low cost X-band polarized radar by installation of test observation net which are composed of small X-band polarized radars in Oklahoma [2]. A project to improve observation range of regular C-band radar observation net of the National Weather Service is conducted in Japan by installing three X-band polarized radars by NIED (national research institute for earth science and disaster prevention) as a part of TOMACS. These studies considered geographical and climate characteristics of local area and conducted to improve quantitative radar precipitation assumption by utilizing radar observation net, which are actually installed, as much as possible.
Geographical characteristics should be thoroughly considered in order to develop QPE algorithm appropriate for circumstance in our country [1]. QPE is a Z-R relational equation to estimate the strength of precipitation with a relational equation (Z=ARb), a parameter A is constant and b is quotient in the equation) which expressed the relation of reflectivity toward precipitation particles, Z, and ground rain rate, R, as series of power function. Generally, Z=200, R=1.6 by Marshall and Palmer’s method[3] is used but deduction of various - relational equation is available according to the precipitation type and space-time [4].
In some studies, to address this problem, the parameters of the relationship were estimated and corrected before heavy storms came from the sea to inland. Henschke et al. (2009) analyzed the past data with a temporal resolution from 1 h to 24 h to supplement insufficient ground rain gauge data[8]. Rendon et al. (2011; 2013) conducted a study to correct the parameters of the relationship before heavy storms came into the ground rain gauge observation network in the South Florida Peninsula [9-10]. In that study, a Kalman filter was used to estimate a mean field bias of the radar rain rate, which was then used to calibrate the parameters of the previously estimated relationship. However, both studies relied on the past data, rather than prior information on the forthcoming storm in real-time. Therefore, when they are to be used in real-time, the methods used in both studies have limitations. With regard to Kim’s method [5], most of precipitation comes through sea side and get into inland which is quite difficult to get ground hyetometer as our country is a peninsula in which three sides are covered with sea. Therefore, mean-field bias correction is difficult while assumption of parameter in Z-R relational equation is impossible as it is extremely hard to collect ground hyetometer data before precipitation gets into the inland and in the initial period of precipitation generation [6-7]. Preset single Z-R relational equation is solely available in this period after all.
To overcome the limitation with which current radar network system and quantitative precipitation estimation faced, this study suggests a novel algorithm of quantitative precipitation estimation to improve the accuracy of rainfall estimation in the Korean Peninsula. For this purpose, this study focuses on (1) development of the algorithm of common region quantitative precipitation estimation utilizing overlapped observation area of radars and (2) verification of the usability of the algorithm to a coastal area. The algorithm employs more than two radars sharing overlapped observation area and ground observation network. We chose the southern coast where precipitation entered from seaside is quite frequent and used Sungsan radar installed in Jeju island and Gudoksan radar installed in the southern coast area. We used the rainy season data generated in 2010 as the precipitation data.
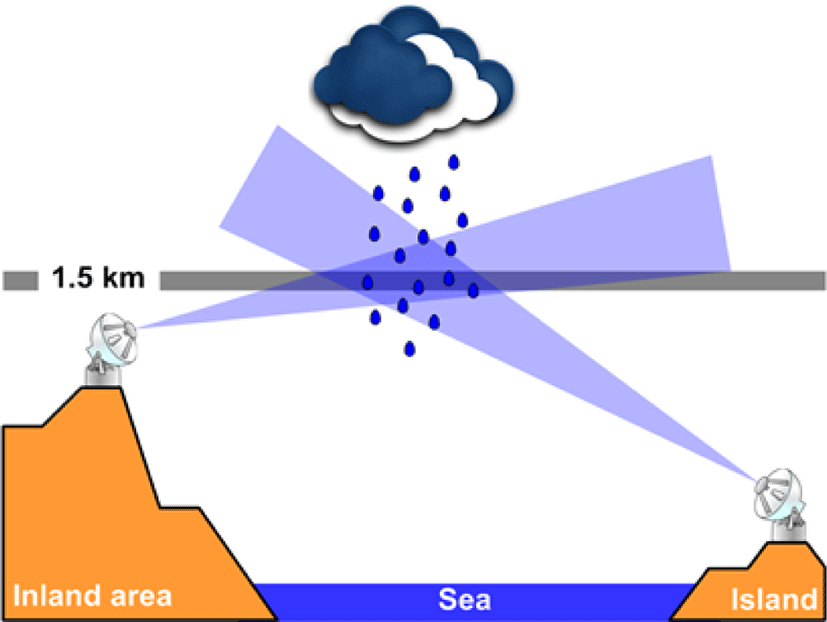
If there is an area in which two or more radar observation radius are overlapped, we call the area as an overlapped observation area. The overlapped observation area could be quite wide depending on the radar observation radius and it could also occur either inland or sea. The overlapped observation area in which two or more radar observation areas are overlapped allows collecting radar observation data twice. Therefore, the utilization of overlapped observation area is crucial in order to increase the practical use of the radar observation system and to complement shortcomings.
Fig. 1 shows a schematic view of the common observation region reflecting the installation environment of the radars located in Jeju and South coast. Like Fig. 1, it is almost impossible to install the radar at the same altitude in the mountainous region that occupies most of the country. Therefore, most radars are installed at different altitudes. If the observations characteristics of two radars are different from each other, mutual bias will occur in the reflectivity data between the two radar, observed in the common observation region. The reflectivity bias between two radars is usually caused by radar observation direction, radar elevation, heavy rain direction, abnormal propagation, correction factors and parameters of radar equipment. In addition, due to the cause of these biases, the bias of the reflectivity between two radars in the common region may differ depending on the region and the storm events. In case the common observation region such as Jeju Island and South Coast region exists in the sea, it is not possible to verify the data on the ground because of the inability to use the terrestrial rainfall data. The rainfall estimation for the common observation region is not much different from the existing quantitative rainfall estimation process. The rainfall field is generated by quantitative rainfall estimation for each radar point, and the rainfall for the common observation region is simply determined by the arithmetic average calculation.
The application of this arithmetic average method is also a cause of secondary radar rainfall estimation error because it does not consider the bias of reflectivity between radar points at all. Moreover, it is very likely that underestimation and overestimation of radar rainfall will occur at a time when the parameters of the relationship are difficult to estimate, such as at the initial stage of heavy rainfall.
II. METHODOLOGY
Estimation of quantitative precipitation in Korea is a limited method using relational expressions, and it has it limitation in special areas such as coastal areas. In order to compensate for the limitation due to such geographical influences, we developed the algorithm of CRQPE (common region quantitative precipitation estimation) method. For reference, a general quantitative precipitation estimation method applied in Korea is described by [1]. Fig. 2 shows the mimetic diagram for typical rainfall observations of radar and surface rain gauges in the southern sea and southern coastal regions according to heavy rainfall movement for describing the CRQPE method. 2, and Table 1 summarizes the observations and estimates of rainfall in the Jeju and South coast regions of each stage according to the movement of heavy rainfall.
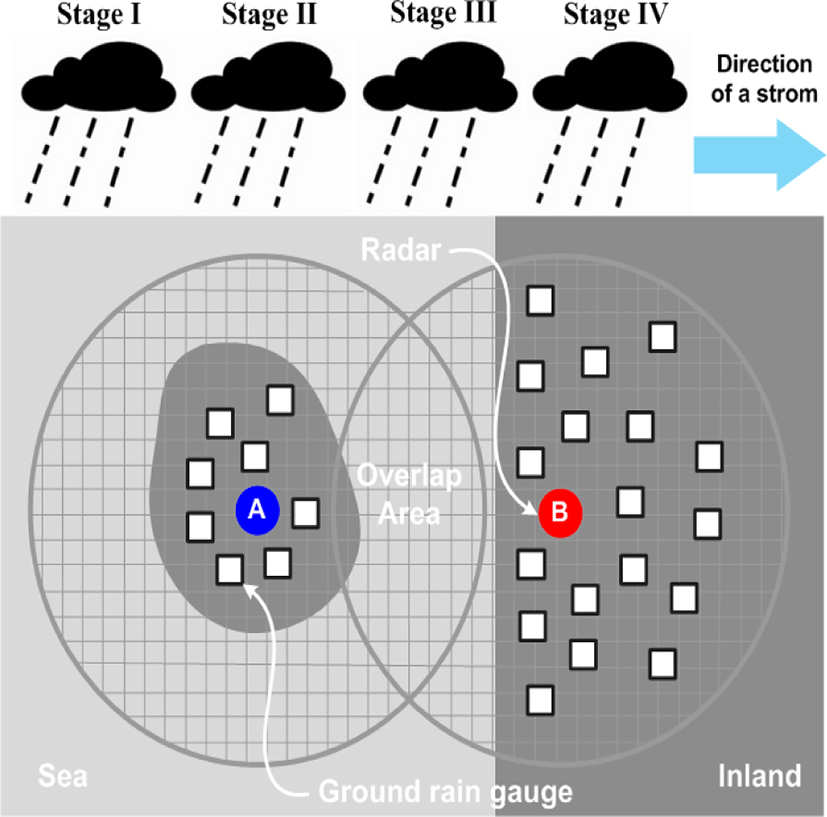
For convenience of explanation, the radar that observes the heavy rain ahead is defined as ‘Radar A’ and the next radar is defined as ‘Radar B’.
Considering the currently installed radar model, the algorithm is constructed for the purpose of the application of single polarized radar.
However, since it is time prior to collecting the ground level rain gauge data that can be used for the rainfall estimation of Radar A, quantitative rainfall estimation is performed using the existing Z-R single relational equation only. The reflectivity observed in Radar A is transformed into rainfall intensity, using Z=200R1.6 or Z=300R1.4 which is typically used. Of course, this method is one of the causes of poor quantitative quality of radar estimated rainfall, but it is the best in the present situation where there is no data of groundwater gauge.
Stage II is also a step that can be observed in the rain gauge installed in observation radius of the radar A. At this stage, Quantitative Precipitation Estimate (QPE) using the reflectivity of Radar A is possible. Therefore, it is possible to estimate the coefficient of mean-field bias correction of radar rainfall as well as real-time determination of the Z-R relational parameters. On the other hand, it is impossible to observe rainfall with Radar B.
In this study, the least squares method was applied as a real-time quantitative precipitation estimation method for the cases where the ground rain gauge data were sufficient. The least squares method is easy to apply, and it is possible to calculate the parameters of the appropriate relational equation when the surface rain gauge has sufficient data.
The procedure for deriving the parameters of the equation using the least squares method is the same as one described in [1].
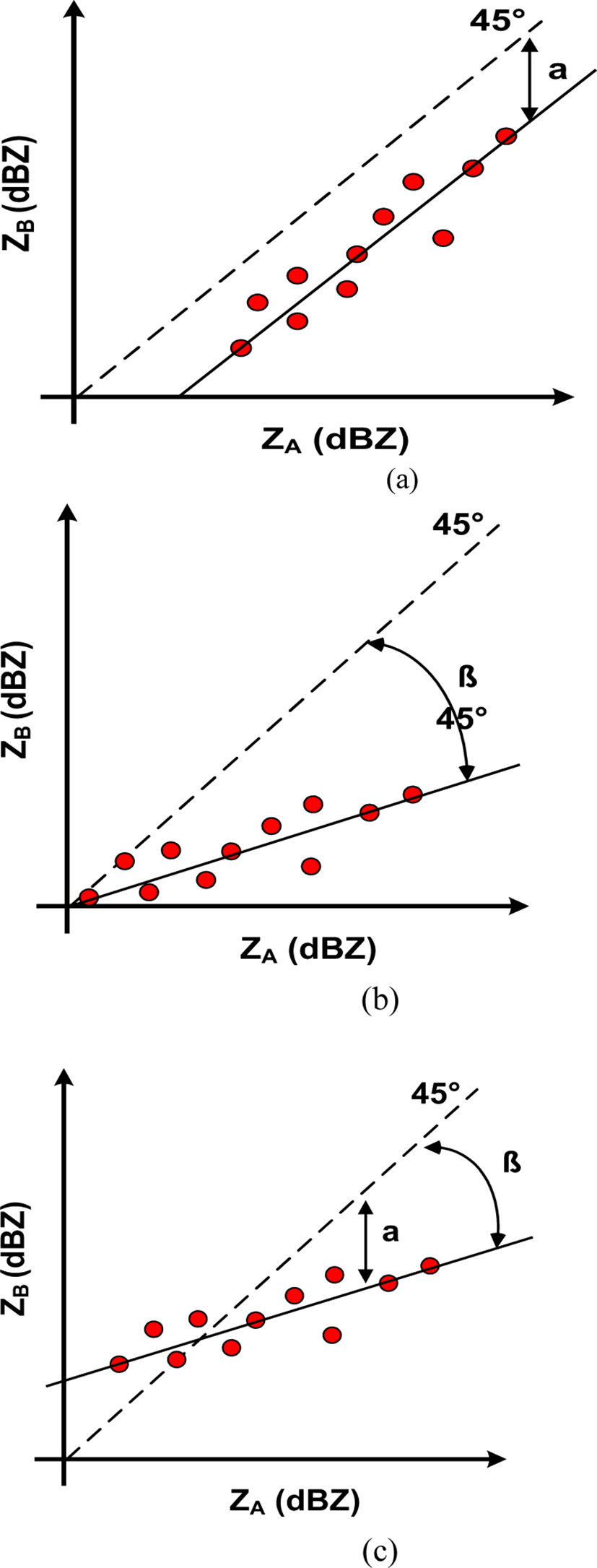
The Stage III is the point at which the common observation region of both radars occurs. In other words, rainfall can be observed jointly for the same storm. Only at this stage, it is possible to confirm the difference in reflectivity between two radars. In addition, the relative error between two radar reflectivity data is checked and estimated. Fig. 3 shows various types of error between two radar reflectivity. The shape of the error is shown in Fig. 3. As shown in Fig. 3, the error type can be determined by mutual comparison (scatter plot) through the two radar’s reflectivity.
If the error type appears as bias like Fig. 3 (a), it can be estimated relatively easily. However, since it is the initial point of the occurrence of the heavy rainfall, it is difficult to obtain the data of the ground rainfall system enough to accurately estimate the parameters of the relational expression. Therefore, it is possible to estimate the radar rainfall using the existing single relational expression. From the time when the ground rain gauge can be sufficiently secured, more accurate radar rainfall estimation becomes possible by updating the real-time relational expression.
When relays calibration is made for the parameters of the two radar sites, consideration should be given to the equations described above.
First, defining the site’s radar to transmit the parameters of the relational expression as ‘A Radar’ and the radar to be transmitted as ‘B Radar’, the correction factor can be calculated as follows. Such a correction factor is applicable when there is only a bias between two radars.
Where α is a bias correction factor for the two radar reflectivity, ZA is the reflectivity of the radar observing the rainfall, and ZB is the reflectivity of the radar observing the rainfall for the second time. The linear regression process using the existing least squares method considering this correction factor α is as follows. Eq. (2) is the parameter b, Eq. (3) is a summary of the intercept.
As a result, if there is only bias between the two radars, the parameters b are the same. On the other hand, the parameters A should be calibrated sequentially considering the bias as in Eq. (4) below.
III. APPLICATION DATA
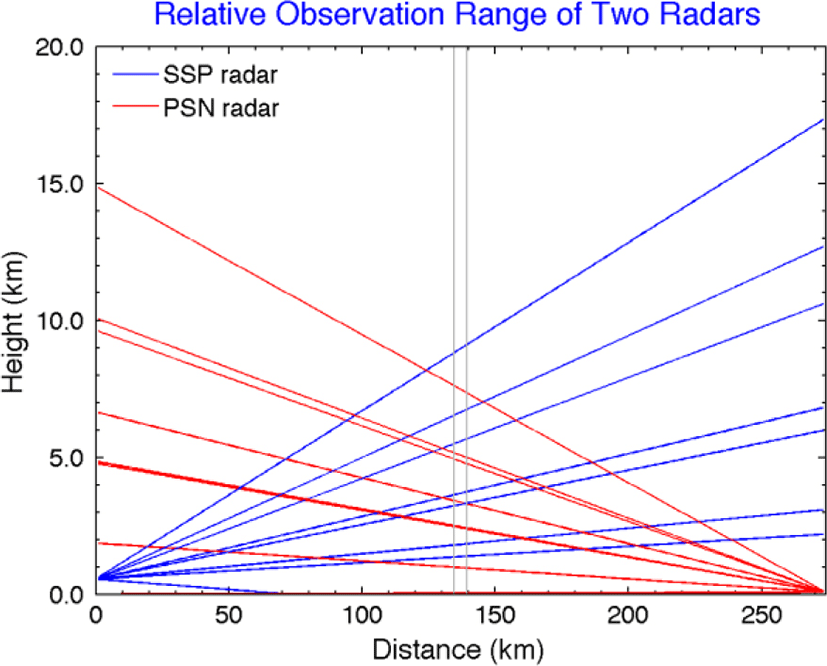
The observation radius, common region, and surface rain gauge applied to Sungsan and Gudoksan radar points are shown in Fig 4. The radar parameters are summarized in Table 2 shows that the distance between Seongsan radar and Gudeosan radar is about 274 km. Therefore, the observation radius with at least 137 km should be used to establish the joint observation area of these two radars. The number of the ground level gauges (only for AWS in the Meteorological Agency) within the 180 km observation radius of Seongsan radar is 83 (Gosan Center, Jeju Airport, Jeju, Gosan, Seongsan, Seogwipo, Jungmoon, Ara, Hawon, Chooja Island, Woo Island, Mara Island, Yoosooam, Seonheul, Seogwang, Erymook, Hanlim, Namwon, Kujwa, Seongpanak, Pyoseonmyeon, Moseulpo, Gapa Island, Azalea field, witsaeoreum, typhoon center, Jigwi Island and 56 others).
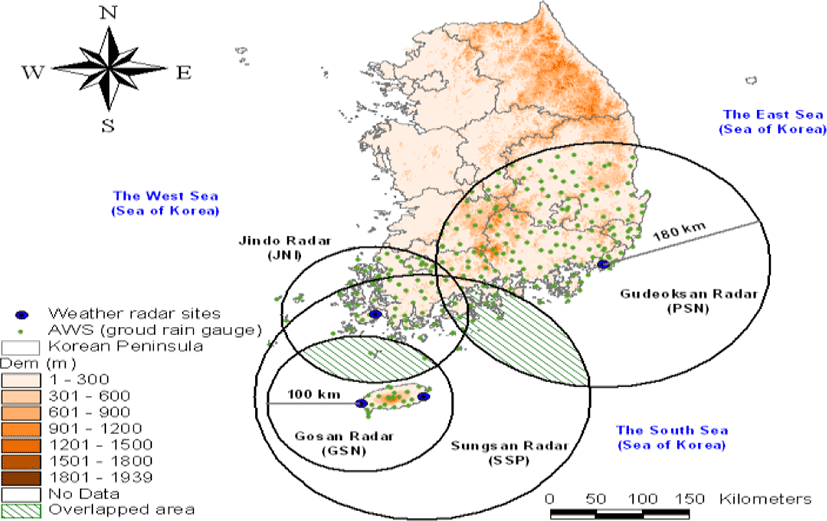
In Korea, CAPPI is used for the purpose of quantitative precipitation estimation, and usually 1.5 km is used due to mountainous terrain and high-rise buildings. However, in this study, when using CAPPI (constant altitude plan position indicator) data, it is physically difficult to select appropriate radar Bin between two radars, so we used radar data which has the shape of the (PPI).
Fig. 5 is a schematic diagram of beams overlapped on the common observation region using the position, height, distance, beam width, and elevation angle between two radars. In this study, we selected Bin necessary for the calculation of radar reflectivity considering radar angle and radar distance.
In this study, a total of two storm events were selected for the application of the CRQPE method. Table 3 summarizes the duration of storm event, storm surveillance radar points, and application scenarios. The selected storm events are typhoon cases that penetrated the southern coast region. The period covered storm events which occurred during the year 2010, and the radar point which was actually influenced by the storm events can be confirmed through Table 3.
| # Event | Storm | Scenario | |
| Period (mm/dd/yy hh:nn) | Type | ||
| 1 | 06/11/10 06:00 - 06/12/10 23:00 | Monsoon | SSP->PSN |
| 2 | 07/10/10 10:00 - 07/12/10 04:00 | SSP->PSN | |
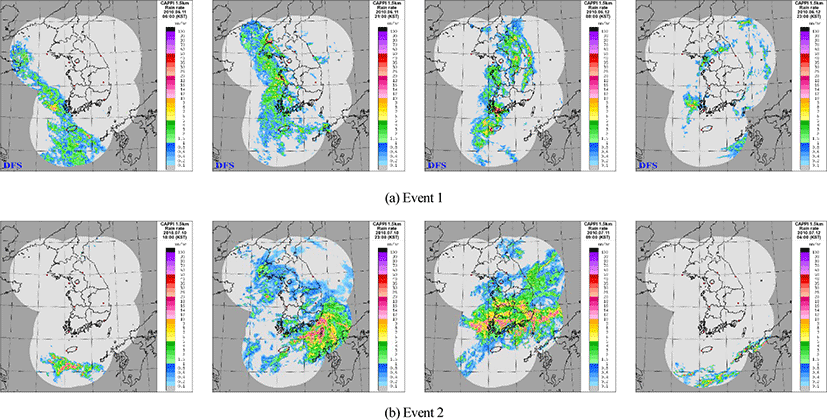
The rainfall field of the storm event is shown in Fig. 6 to ascertain the route of the storm and the type of storm in the storm event. The storm event 1 and 2 applied in this study are types of storm event which occurs frequently in the rainy season, and storm event which moves from the southern coast to the inland.
IV. APPLICATION RESULT
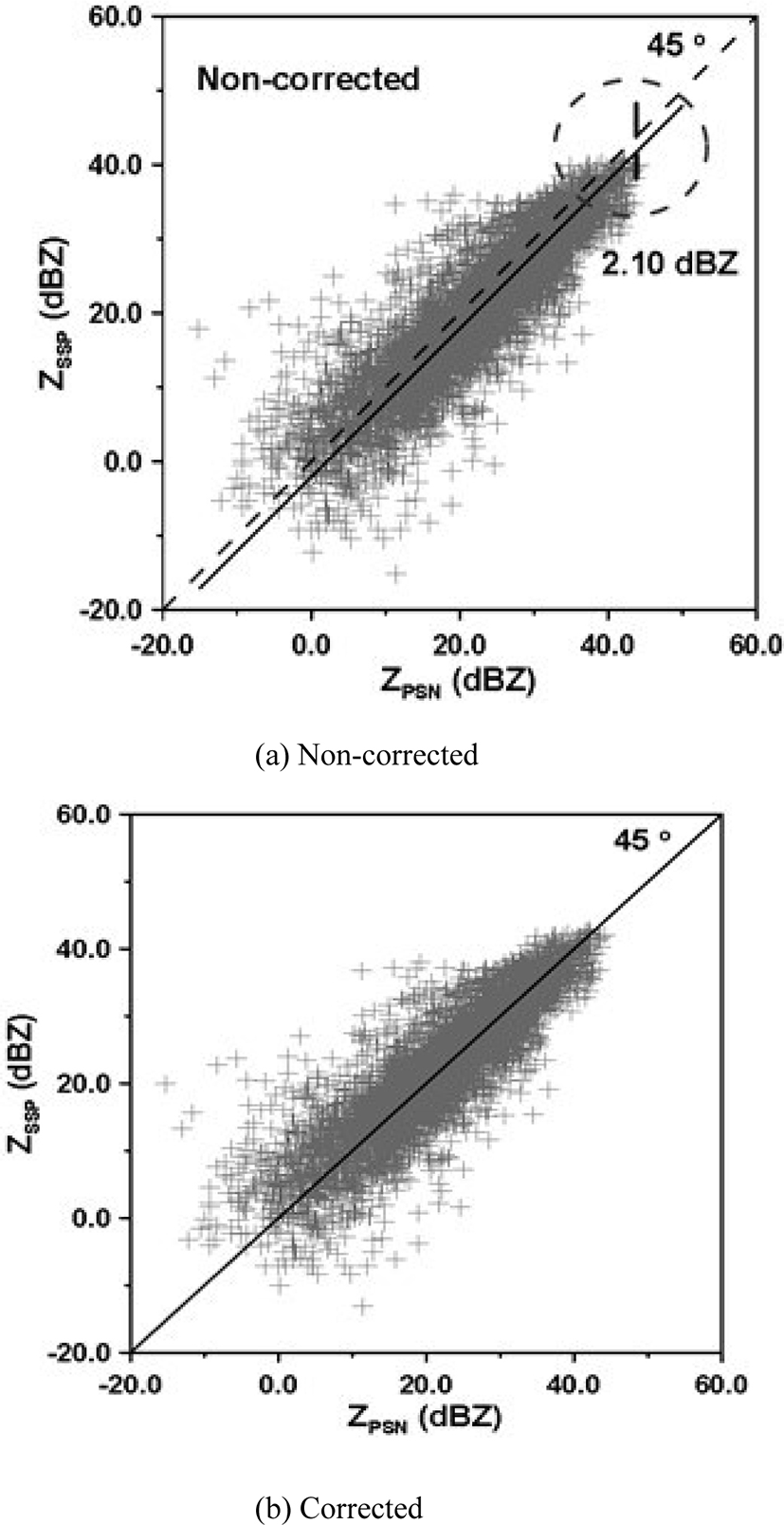
The two types of radar reflectivity data were compared with each other to find error type. Fig. 7 is a scatter plot for the reflectivity of the Sungsan radar and the Gudoksan radar. This study corrected the bias of two radars, SSP and PSN, using simple mean field bias correction method described in [1]. First, Fig. 7 (a) shows the scatter diagram to confirm the bias of radar reflectivity between two radar points. As a result, the two radar reflectivity data were compared with each other, and it was confirmed that the difference in reflectivity data appeared as bias which is systematic error. In the case of Fig. 7 (a), the reflectivity (ZSSP) of the Seongsan radar is less than the reflectivity (ZPSN) of Gudoksan radar, which is 2.10 dBZ.
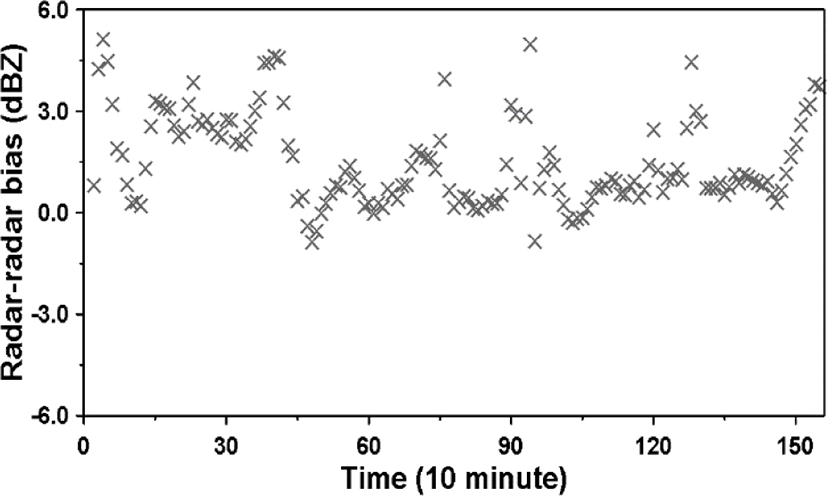
Fig. 7 (b) shows the results obtained by correcting the bias between radar points by the simple correction method. Here, the simple correction method is to set the specific radar point data as a reference value and to correct as much as the bias which occurred in the other radar point data. In the case of Seongsan and Gudoksan radars, most of the heavy rain moved to the Gudoksan radar through the Seongsan radar, and the Seongsan radar data was set as the reference value. The calibration result shows that the average deviation between the two radar reflectivity is eliminated by correcting the bias of 2.10 dBZ before correction. In order to examine the bias between the radars according to the change of time, the bias was calculated every hour. Fig. 8 is the result of estimating the bias of the reflectivity of Sungsan and Gudoksan radar every hour.
The results show that the bias between radars occurs in the range of -1.0 to 6.0 dBZ. The mean is 1.50 dBZ and the standard deviation is 1.44 dBZ. Particularly, this variability can be divided into Part A (0-400 minute) and Part B (400-1500 minute) time points of the storm events observed in the common observation region. The average of Part A is 2.48 and the correction factor was calculated in real time to correct the inter-radar bias.
In Fig.9, the box means the number of ground level rain gauge points available for the parameter estimation of the Z-R relational equation at the point, ASSP and APSN are the parameter A estimated by the existing method with respect to Sungsan and Gudoksan radar points, and ACRQPE is the parameter of Z-R relational equation, which is estimated in existing way by CRQPE method ZR relation.
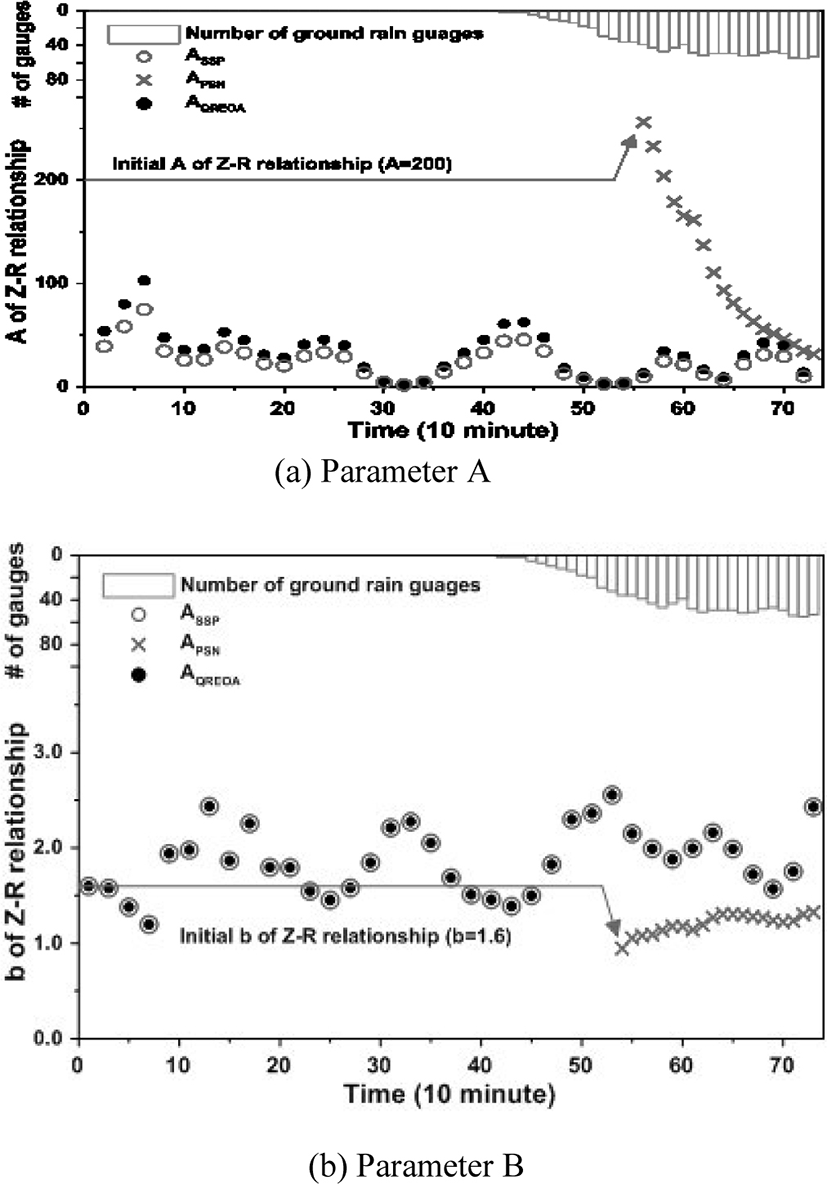
When there is not available ground level rainfall gauge and there is not sufficient data to estimate the parameters of the Z-R relational equation, the parameters of the Z-R relationship are constantly applied with a specific relational equation (A = 200, b = 1.6). Therefore, the parameter A of 200 is constantly applied until the time point of 55. Then, when the ground water gauge data become sufficient, it becomes possible to estimate the parameters as shown in Fig. 9 (a). However, the estimated parameter is decreasing to a certain value at the initial stage of the heavy rainfall, so it is considered that the uncertainty is large.
On the other hand, the CRQPE method is able to estimate the parameters of the Z-R relational equation from the point at which the calculation and correction of the bias between two radars is possible. Therefore, it has an advantage that the parameter can be estimated before the heavy rain enters inland. In addition, it can be seen that the parameters are estimated more reliably than the existing method regardless of the quantity of the terrestrial rain gauge data at the initial stage of the influx of inland. In addition, we can confirm that the estimated parameters of both methods converge to similar values from the point of time of 67 when the surface rain gauge data are sufficient. Fig. 9 (b) is the result for parameter b.
As shown in Fig. 9 (b), the existing method applies a parameter of 1.6 to the point at which the groundwater gauge data are acquired.
In the case of the CRQPE method, the bias correction between the actual radar only affects parameter A of the Z-R relational equation, so the parameter b can use the previously estimated parameters as is. In the case of Seongsan and Gudoksan radar, the parameter b applied to the Gudoksan radar point is an estimated value with sufficient ground water gauge data at the Gudoksan radar point.
In general, the Z-R relationship, like Marshall-Palmer’s equation, is one of the underestimated results of radar rainfall. In addition, even though the groundwater gauge data, which can estimate the parameters of the Z-R relational equation, have been obtained, the number is only the minimum number that can be used to estimate the parameters of the Z-R relational equation. In conclusion, when real-time parameters are estimated, uncertainties due to insufficient number of groundwater gauge data are very likely to be implied. Also, it can be considered as a problem that can be seen in estimating the quantitative precipitation by a single polarized radar.
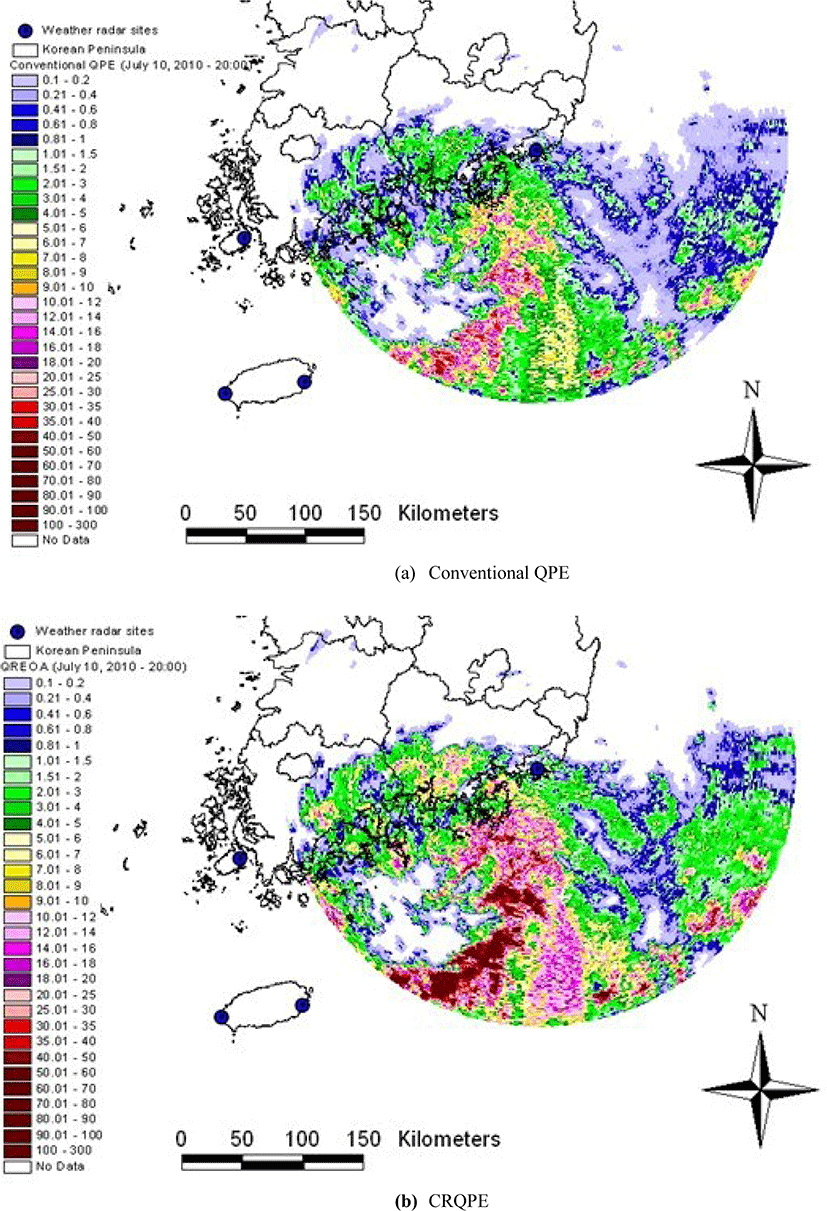
The results of applying the CRQPE method of Fig. 10(b) showed better results than the radar estimated rainfall by the conventional method. Under 15 mm/hr, radar rainfall was estimated based on the rainfall intensity of the ground rainfall gauge, and radar rainfall was estimated appropriately at 15 mm/hr or more. This is because the appropriate parameters of the Z-R relational equation can be estimated and applied from the initial point of time when the heavy rain enters the inland. Furthermore, in the CRQPE method, the better result is expected to be produced since the bias between the radar rainfall and the rainfall by the ground rainfall system is also considered in real time in the quantitative rainfall estimation process. A typical cause for such a result is the constant Z-R relational equation used at the beginning of the storm.
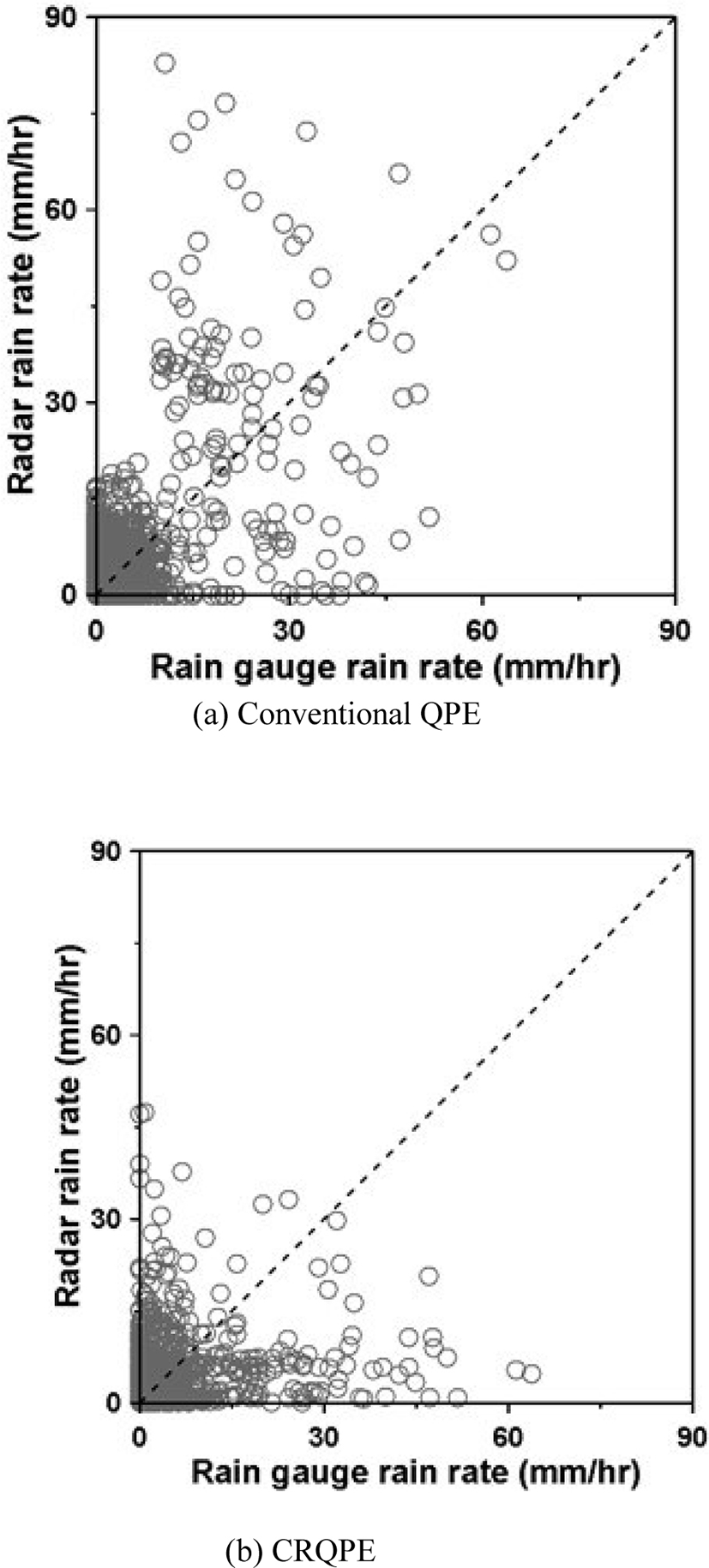
Fig. 11 shows the radar rainfall field at the time when the heavy rain enters inland. Fig. 11 (a) is the estimation result by the existing method, and (b) is the estimation result by CRQPE. If the existing method and the CRQPE method are examined together, it can be confirmed that the existing method underestimates rainfall compared with the CRQPE method. In particular, for rainfall above 20 mm/hr, the difference in the quantitative estimation results of the two estimation methods becomes clear. Based on these results, it can be concluded that the difference is larger when the same heavy rainfall occurs in urban and natural river basins in coastal areas and these differences are expected to have a significant effect on the outflow.
V. CONCLUSIONS
In this study, CRQPE is proposed to estimate the quantitative rainfall in the coastal area using geographical and climatic characteristics and radar observation network in Korea. For this purpose, we use the common observation region of the domestic dense groundwater gauge network and the radar observation network, and selected the southern coast region as the target area. We used Seongsan radar installed in Cheju Island and Gudoksan radar installed in the southern coast region. As heavy rainfall data, the rainy season data in 2010 was used. The results are summarized as follows.
(1) Two radar reflectivity data in the common observation region were used to confirm the existence or absence of bias which is the systematic error between the radar. At both application radar points, it was identified, and the degree of bias varied from site to site. In addition, it was confirmed that the bias varied over time. Based on these results, the correction factor of the inter-radar bias was calculated. There are various reasons for the occurrence of bias between radars, but the radar observation equipment model, installation characteristics, and observation environment seems to be the most important factors.
(2) It was found that when the parameters of the real-time Z-R relational equation are estimated by the CRQPE method proposed in this study. The CRQPE method can compensate the weakness of the existing method. The first is that the parameters of the Z-R relational equation can be estimated before the inland inflow of heavy rainfall. The second is that it is possible to estimate the parameters of the Z-R relational equation irrespective of the number of terrestrial rainfall data at the initial time after the inland inflow of heavy rainfall. The strength of this CRQPE method is to improve the accuracy of quantitative estimated rainfall in areas sensitive to heavy rainfall like coastal areas.
(3) As a result of estimating the quantitative rainfall by two methods, the radar rainfall estimated by the conventional method is underestimated than the rainfall intensity of the ground rain gauge over 15 mm / hr. This result is produced since a single Z-R relational equation is applied due to the lack of data on the groundwater system at the beginning of the storm. On the other hand, the rainfall intensity estimated by the CRQPE method was found to be a reasonable estimate of the quantitative rainfall over the entire rainfall intensity range.
The suggested CRQPE method is a novel algorithm for the peninsula and/or island regions which face with the limitation of quantitative precipitation estimation due a storm commonly coming from sea side and going through the inland. The Korean Peninsula applied in this study is a highly developed area in weather station network such as ground observations, and the algorithm showed the usefulness of the algorithm in this area. It might have a limitation in some area having a poor ground observation density. This study applied the algorithm to single polarization radars, but it has an infinite of potential that can be applied to dual polarization radars.