I. OBJECTIVES
Microwave attenuation by tree foliage should have a strong link to water content in leaves. Using a network analyzer, we sampled natural broadleaves, including Japanese cinnamon, and investigated their effects on microwave (3-20 GHz) frequency characteristics. Microwave attenuation is proportional to the amount of water held within leaves. Light energy reacts with water and carbon dioxide to synthesize oxygen and sugar inside the leaf (photosynthesis). Thus, leaf water content is a parameter of the leaf’s capacity to absorb carbon dioxide. The technical developments described here will enable the visual representation of plant health.
II. BACKGROUND
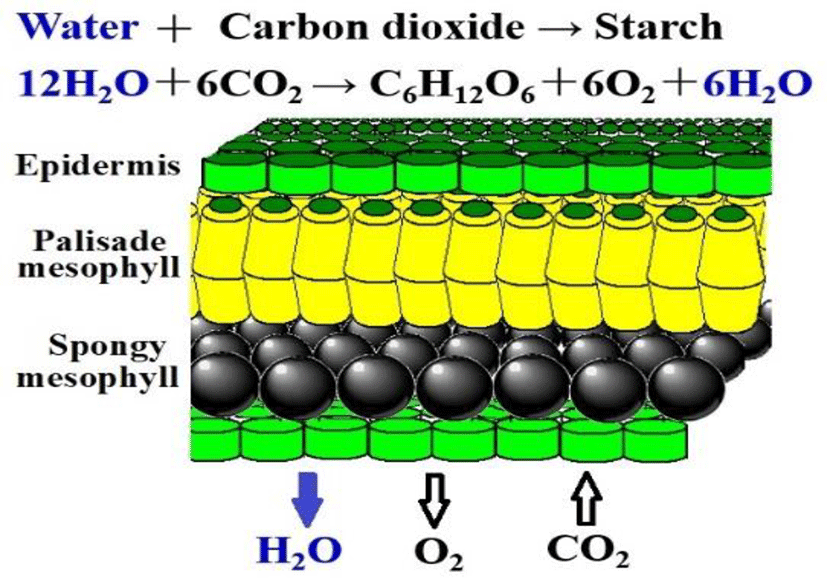
The leaf of a broadleaf tree generally consists of two structures: the palisade mesophyll and the spongy mesophyll. The spongy mesophyll tends to be replete with moisture and helps produce oxygen from carbon dioxide and water in response to sunlight through the chemical reaction of the leaf known as photosynthesis. To evaluate carbon dioxide consumption, it is important to measure the amount of leaf moisture. Reducing airborne carbon dioxide has emerged as a worldwide issue. We can predict, based on certain measurements, how effective trees will be in absorbing airborne carbon dioxide. The extent to which carbon dioxide is converted into oxygen is determined by the average amount of moisture in the leaf and the number of daylight hours. Figure 1 gives the chemical formula for photosynthesis.
III. EXPERIMENTS
In the experiment, there are two different distances between the transmitter and the receiver: near-field propagation and far-field propagation.
Given our preference to deploy two transducers face to face at a short distance across the leaf, we will discuss the near-field propagation of electromagnetic waves. The quantitative definition requires use of Maxwell's equations to calculate that electromagnetic waves are generated when an electric charge accelerates, a complex process for which a simplification is provided here. An overview is provided below.
Calculations of the magnitude of the electromagnetic field, assuming that the distance from the radiation source is r, produces a term proportional to 1/r, 1/r^2 , 1/r^3 (each term representing a radiation field), and 1/r^2: an induction field (a component according to Biot-Savart's law), 1/r^3: a Quasi-electrostatic field (referred to as an electric field by a dipole). In the far field (where r is large), the term proportional to 1/r^2 and 1/r^3 approaches zero more rapidly than the term proportional to 1/r, leaving only the term of 1/r.
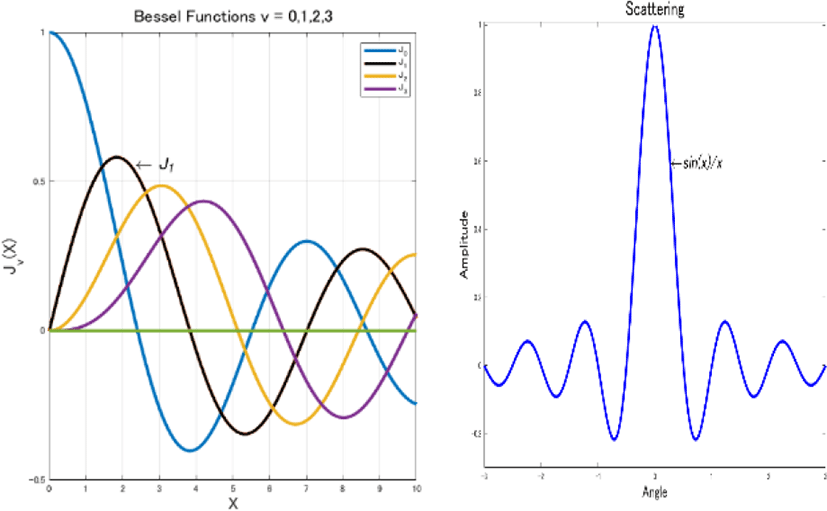
Calculating the boundary of the near field and far field gives the value λ/2π (where λ is the wavelength of an electromagnetic wave). Specifically, at 2.5 GHz, a distance of 19 mm or less is close. Waves in the vicinity can be approximated by J1 of the Bessel function (left of Figure 2 and equation 1).
The far field becomes equal to 1/r. As the term proportional to 1/r^2(a component according to Biot-Savart's law_and 1/r^3(a component according to Quasi-electrostatic field due to dipoles) becomes zero, the term proportional is equal to 1/r.
The wave at the far field can be approximated by Equation 2 and by Figure 3. Since x in Equation 2 is an angle(a phase), interference is given to the adjacent space. That is to say, a received power will be non-linear due to influence from neighboring channels by leaves(scatter phenomenon, Figure 3).
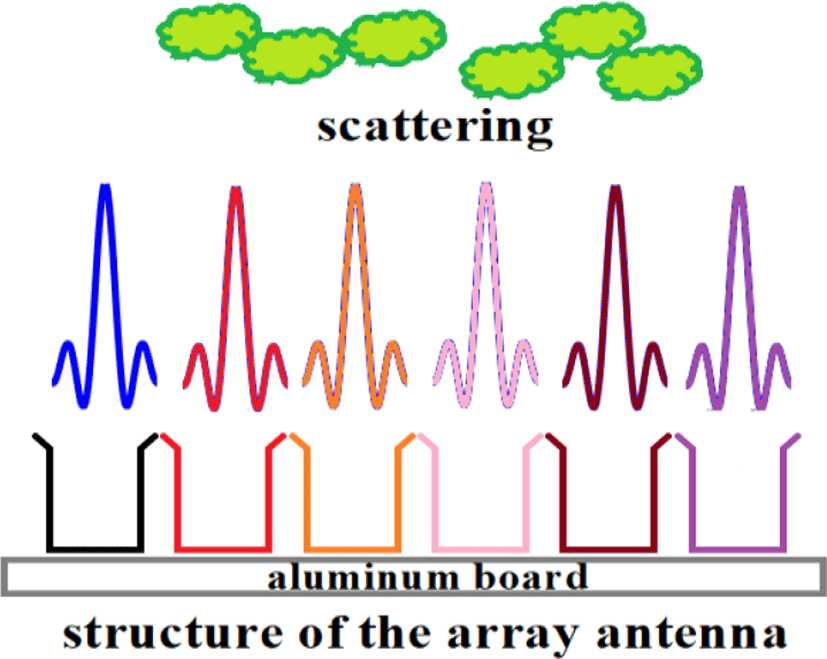
This implies that the adjacent horns have less interference when angles are wider than when they are closer than the distant signal source. In other words, a horn antenna should be near the target tree; otherwise, the interference of the adjacent waves will be relatively strong (right of Figures 2, and Figure 3, Equation 2). Qualitatively, the near field is an area where the wavefront needs to be regarded as a spherical surface, while the far field is an area where the wavefront may be regarded as a plane. The impedance of the wave in the free space is 377 Ω.
The electromagnetic penetration is infinite in a perfectly transparent substance and zero in a reflective material (for example, metals).
Attenuation is obtained as follows:
Equation 4 shows that attenuation increases in inverse proportion to wavelength and increases linearly with frequency.
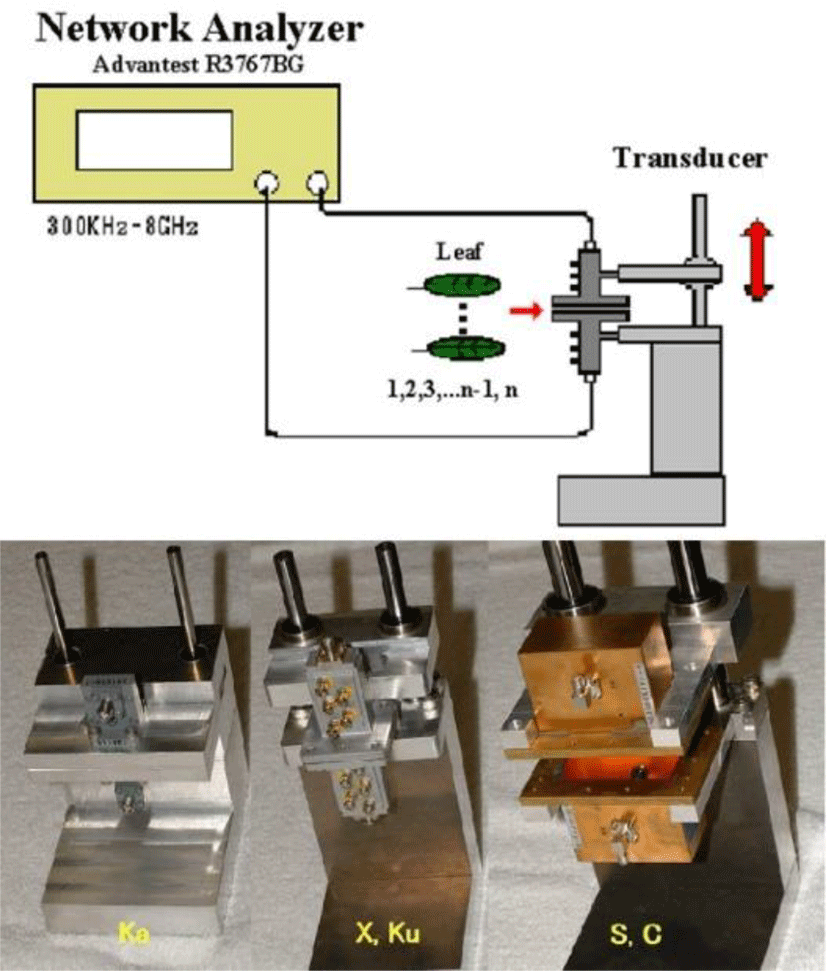
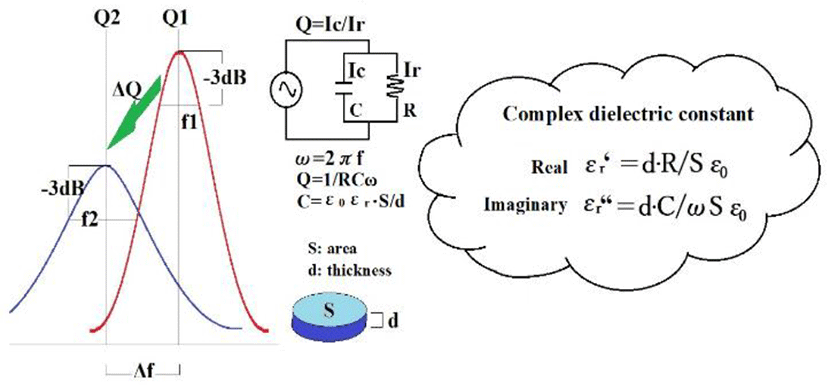
Sandwiching leaves between two transducers, as shown in Figure 4, we measured S, C, and X band power attenuation and S parameters. This configuration is referred to as a split cylinder. Due to the relative permittivity of the leaves, the resonance frequency, Q value, and half-value band differ before and after insertion. Figure 5 illustrates these relationships.
Equation 5 gives the approximate dielectric constant of water. In our experiment, room temperature was set to about 20 degrees (dielectric constant of water at 20 degrees: 80.36).
Since components other than water differ slightly depending on the type of leaf, frequency characteristics (especially the slope of the linear function) differ.
In this measurement, we keep the stem immersed in water until measurement to keep leaves from drying, while at the same time taking steps to ensure the leaves did not contain excess water. We used only the leaf center for measurement. Since this split cylinder pinches the leaves, it is not necessary to cut the leaves from the trunk. The leaves were irradiated with microwaves from the top face (forward direction).
To investigate changes in attenuation, we changed the number of leaves and measured frequency with 1, 2, 3, 4, 5, 10, and 15 leaves. Ten days later, we repeated these measurements to determine changes (if any) in water content and attenuation.
To measure attenuation by leaves, we used a network analyzer (ADVANTEST R3767BG NETWORK ANALYZER [300 kHz-8 GHz]). Since the 8-20 GHz region was not covered by this network analyzer, we also used a signal generator (ROHDE&SCHWARZ SMR-20), delay line (linear phase shifter), and a spectrum analyzer [ADVANTEST R3273 up to 26 GHz].
We connected two opposing transducers for each of the tests (S, C, and X bands) with microwaves directed using a waveguide. Attenuation and S parameters were measured by inserting broadleaves into the gap between the two transducers. The system for securing the split cylinder (manufactured by Tasada Works Inc.) was vertically adjustable to allow fine control of gap width.
The leaves tested were taken from Ligustrum japonicum, Cinnamomum camphora, and Ligustrum iucidum. They were all taken directly from the field in the form of branches bearing leaves and measured immediately after field sampling.
The following figures summarize the experimental results:
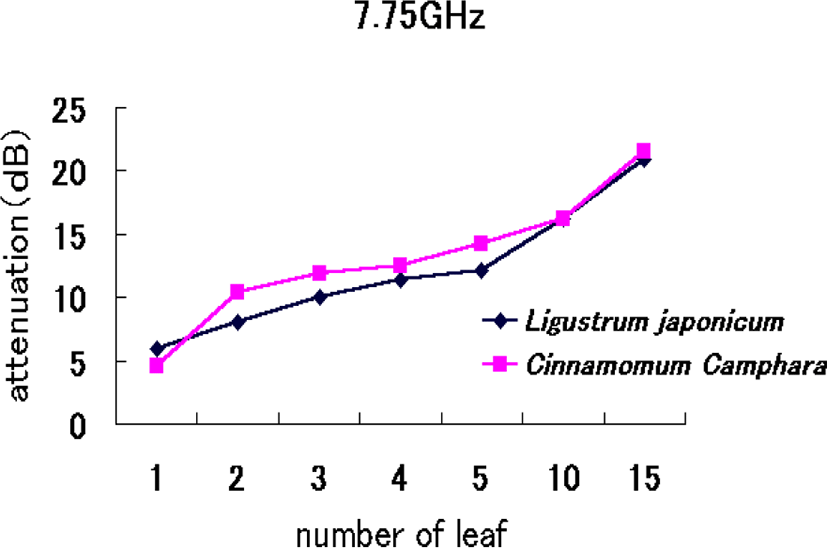
Figure 6 shows attenuation increases linearly as the number of leaves increases, suggesting that microwave attenuation at 7.75 GHz increases linearly with water content.
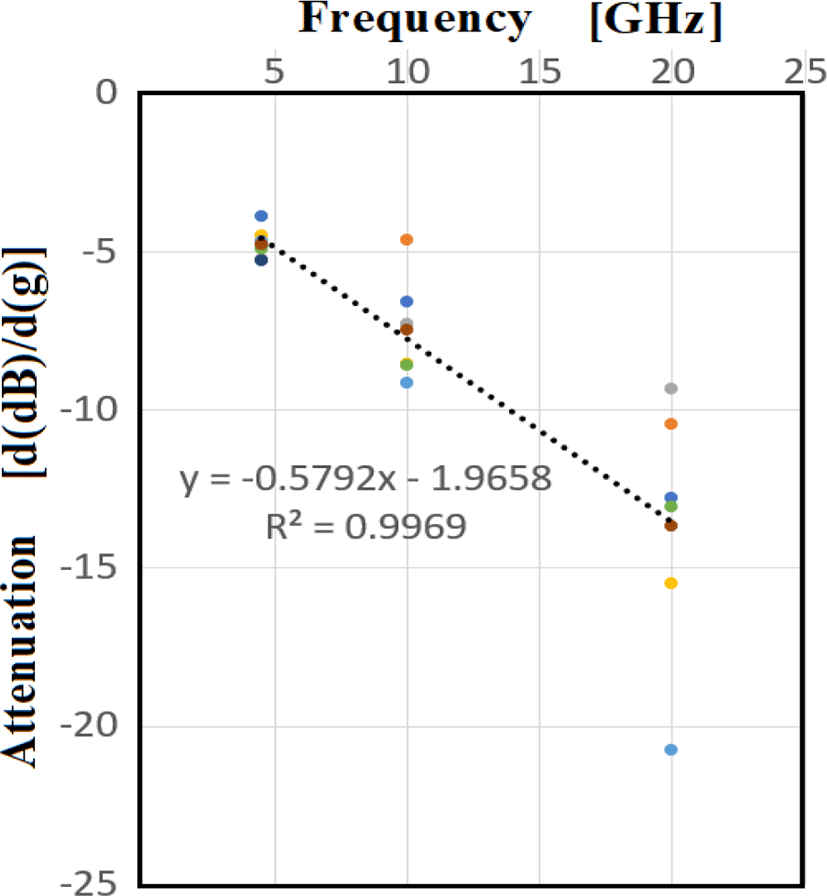
Figure 7 shows the correlation between frequency and attenuation. Although the data in Figure 7 features variations, the average value of each frequency exhibits a linear relationship. Specifically, single leaves are used to assess the fresh state and a slightly dried state. This indicates that attenuation per unit gram is a linear function of frequency, consistent with Equation 4. Table 1 presents the function and correlation coefficient indicating linearity for each plant species.
| Plant | Slope factor | R2 |
|---|---|---|
| Cinnamomum camphora | -0.33 | 0.89 |
| Ligustrum japonicum | -0.31 | 0.92 |
| Hydrangea macrophylla | -0.45 | 0.99 |
| Prunus × yedoensis | -0.15 | 0.95 |
| Meratia praecox | -0.25 | 0.71 |
Although 20 GHz is considered to provide high resolution due to its short wavelength, the phase is unstable. The average of these values is consistent with the prediction formula, but, as Figure 7 indicates, it cannot be put to practical use.
IV. DEVELOPMENT
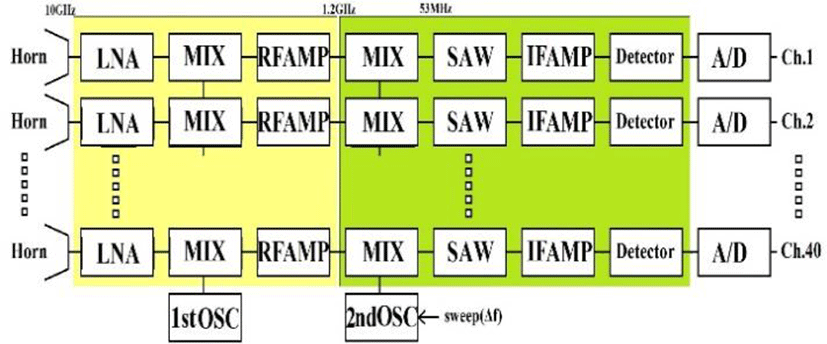
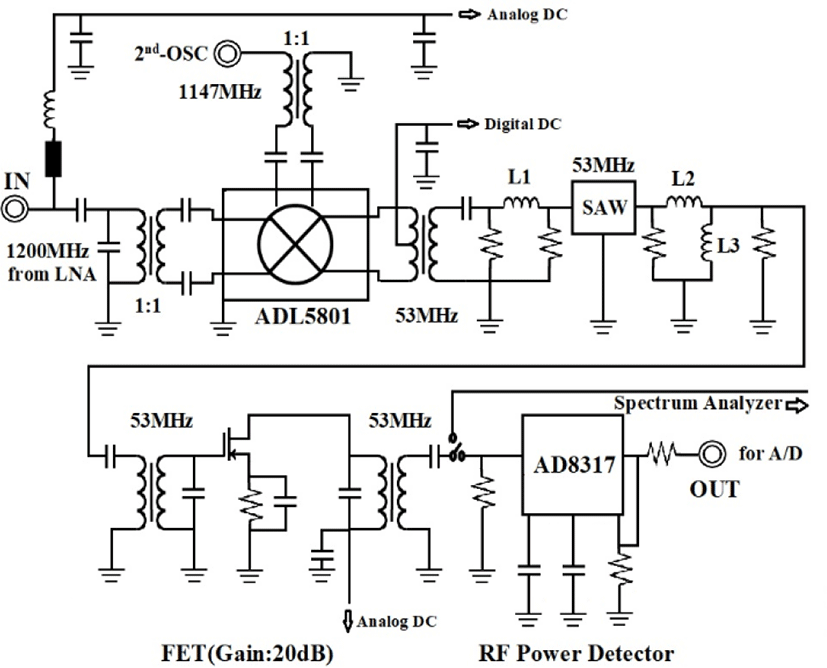
Figure 8 is a block diagram of the prototyped scanner. This device features 40 superheterodyne receivers at 10.5 GHz to detect non-modulated (continuous carrier with sweeping the frequency 300MHz) signals from transmitters located 5-30 meters distant. Since 40 units share two local oscillators, they are all in phase. Here, without the phase difference, the attenuation of the amplitude is obtained by RF detectors with a log amplifier. Figure 9 gives the circuit diagram of the main board. As a reference before an experiment, a signal is received in free space without obstacles in order to set the signal level at zero. In parallel, references with 40 logarithmic detectors are performed with a spectrum analyzer. Each error is managed by the CPU as a quick lookup table.
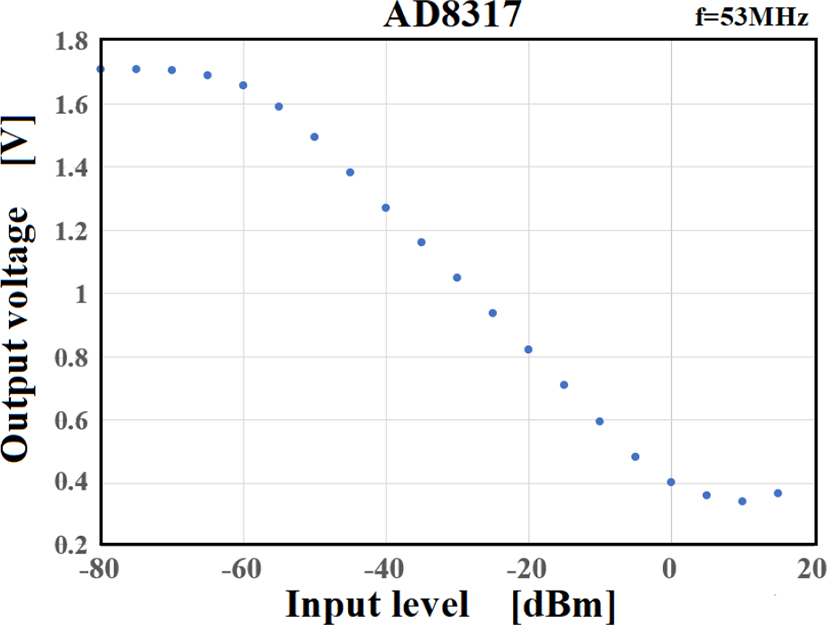
Figure 10 illustrates the relationship between detector input levels and output voltage. As this figure shows, the range from -55 to -5 dBm gives a strong linear dynamic range of 50 dB. We adjusted the transmitter output level and used this linear part.
The elements of the 8-channel 12-bit A/D converter are connected to the CPU by I2C at five elements (8 x 5 = 40 channels) and integrated for 3 seconds at one sweep (Bw:300 MHz) to obtain maximum and minimum values. The A/D sampling frequency was 1,000/sec/ch. The average value of the maximum and minimum will be attenuation scalar value (j part = 0; details to be explained in item 4.2).
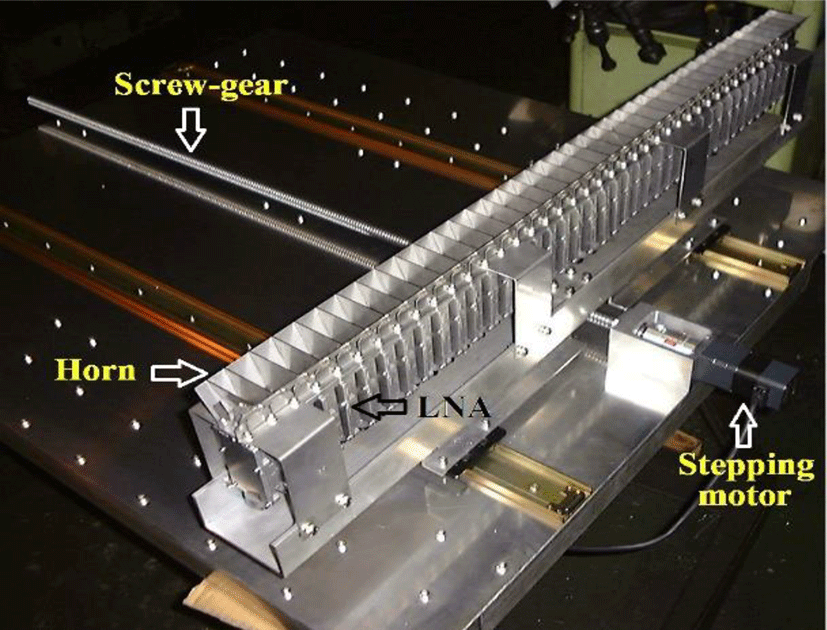
Including the time required for the physical movement of the horn and the integration time of 3 seconds, the time required to render a single raster is 5 seconds. It takes 250 seconds to scan one sheet (40 x 50 pixels).
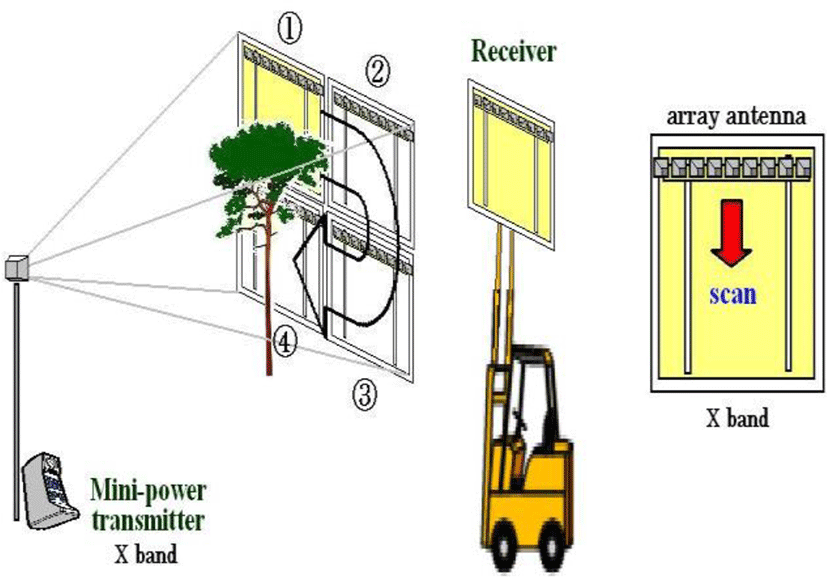
The dimensions of the scanner are 100 cm x 101 cm; the back aluminum plate size is 100 cm x 120 cm, and the sensor can be up to 40 horizontally and up to 100 in the vertical direction (moving in 1 cm steps). The scanner has a standard image quality of 40 x 50 steps and a fine 40 x 100 steps of matrix (Figure 11, 12).
Using a horn antenna provides a gain of 10 dBi (Figure 13). The sensor must be placed as close as possible to the object to obtain the necessary resolution. Using a horn antenna with higher gain suppresses interference from adjacent channels, however, the question arises: Are the beams parallel. Since such physical issues can arise, a gain of 10 dBi may be appropriate at the production stage.
Another solution is to use a higher frequency to sharpen the beam. Here, the dilemma is that a broad dynamic range is needed due to the significant attenuation by the leaves. Based on these conditions, we selected 10.5 GHz.
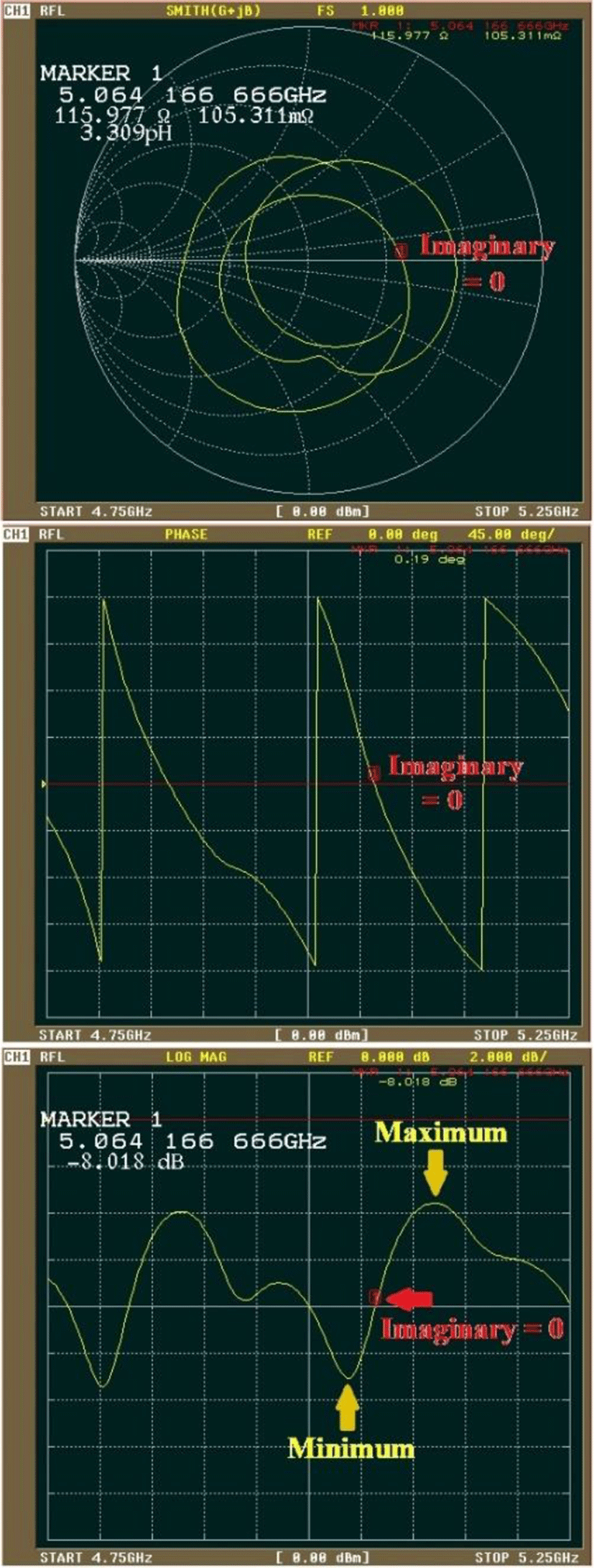
There are several methods for removing the phase part of a signal traveling in free space to assess the power of the receiving signal. It is sufficient to read the signal strength, when the phase part becomes zero. In the Smith chart, if impedance were changed concentrically around Z = 50 + j0 normalized, it would be an intermediate value between the maximum value and the minimum value. In fact, since the image is not rotated concentrically (50 + j0) as shown in Figure 14, a certain degree of error can be approximated in this method. The gradation of the image is a comparison of relative values; if all pixels have the same bias, they cancel out and can be disregarded.
The phase is shifted by inserting a delay line or slowly drifting the frequency of the transmitter. Since the sources are only about 30 m apart obtaining local oscillation frequency with coaxial cable (sweep frequency bandwidth 300 MHz), it is possible to modulate a drifting frequency to the second OSC of the receiver.
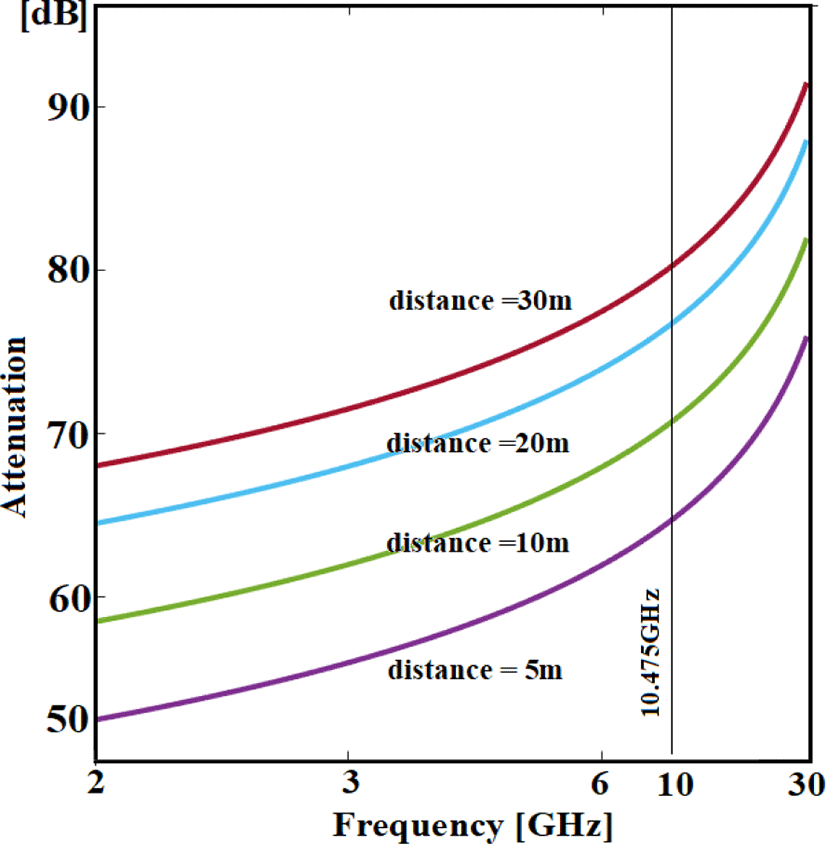
Figure 15 shows free space propagation loss. Table 2 shows the circuit design for a distance of 30 m. The RF detection on the receiver side has a dynamic range about 50 dB, but transmission power must be controlled to avoid saturation and declines in noise level.
In the software, the mechanical control, the value of 40 received power from the A/D converters, and these data are recorded for each raster. Finally, one set of measurement data is saved to an Excel csv file. Table 3 shows the image processing required to display one picture. These functions are provided as reference materials at the end of the paper.
The aluminum plate on the back of the scanner is large (1.2 m x 1 m) and heavy and not readily lifted. As shown in Figure 16, using a lifter, data is acquired on multiple planes (pages). The control of the lister can be controlled in 1 cm increments.
Shown to the right is a picture of the actual tree (Figure 17 left) and a picture drawn for each raster based on data obtained from attenuation through the leaves. Certainly, there is a multi-scatter equivalent to the Loo distribution, but integrated over time, the average value of the phase becomes zero, making it possible to visualize the amount of attenuation. However, the sharpness of the image does not correspond to the optical level, as interference from adjacent channels remains.
The amount of water in the leaves of trees can be quantified in this way. How much water do the leaves of the trees take up?
V. DISCUSSION
As the number of leaves increases, total attenuation increases while attenuation per leaf decreases. We found no significant difference in attenuation per leaf for the different tree species.
This implies attenuation by leaves is not proportional to unit attenuation per leaf or number of leaves and that attenuation per leaf gradually declines as the number of leaves increases. This is probably because the surface resistance differs from the internal resistance in leaves. This difference may affect the S parameters as well.
As the leaves dry out and leaf weight declines over time, microwave attenuation also declines. This phenomenon was more pronounced at higher frequencies and indicates microwave attenuation is significantly dependent on water content. As the data indicates, different frequencies are differently affected by leaves: shorter waves are likely to be reflected at the surface, while longer waves penetrate leaves to some extent.
Based on this data, we developed a foliage scanner for the X-band to assess the status of leaves (Figure 5, 6, 7 ). With a very weak CW carrier from the transmitter in the X-band, 40 array antennas with a receiver can scan and analyze foliage attenuation. We believe this image is something like a chest X-ray image of a tree capable of observing water density in foliage.
Leaves perform photosynthesis to convert light energy into chemical energy, which is then stored in carbohydrate molecules, such as sugars, which are synthesized from the carbon dioxide in the air and the water in the leaves (Figure 1). Annual carbon dioxide absorption (trunk circumference ranging from 15 to 30 cm per tree ) is as follows:
-
Deciduous broad-leaved trees and pines: 100 kg
-
Evergreen broad-leaved tree, needle-leaf tree (other than pine): 66 kg
Leaves containing little water absorb significantly less carbon dioxide. That is, the amount of water contained in leaves is a parameter we can use to predict how much airborne carbon dioxide will be absorbed. Our scanner uses microwaves to assess the amount of water held in the leaves, resulting in a more precise reading of carbon dioxide absorption than the above-mentioned simple method.
Additionally, this foliage scanner can predict the growth of premium seedlings based on the amount of water in leaves or the quality of fruit for premium mangos. For advanced IoT-based agriculture, we believe this scanner will serve as an effective sensor in water management applications.
C-band (3.875 GHz) and X-band (7.75 GHz) wavelengths are 7.7 cm and 3.9 cm, respectively. In general, radiowaves do not pass through objects; rather, they reflect off if the object is deeper than half the wavelength. Meanwhile, radiowaves penetrate objects thinner than 1/4 of the wavelength. If the object is approximately 1/2 the wavelength, both reflection and penetration occur. Thus, microwaves impinge upon trees, S-band waves pass through the leaves, then reflect off the trunks and ground; X-band waves reflect off leaf surfaces; and C-band waves reflect off both leaves and stems and trunks and the ground. Utilizing such property differences between the bands, we may apply SAR to various research efforts (Figure 18): We can collect geographic and geological data used to analyze the distribution of vegetation and the classification of tropical and boreal forests using the S-band, while vegetation pattern data on farmland and grass fields can be collected using the C- and X-band microwaves, taking advantage of differences in reflection intensity between leaves and stems. Combining UWB radar technology and the C and X bands may make it possible to develop a helicopter-borne search and rescue radar system capable of finding humans lost in forests.
VI. CONCLUSION
Microwave attenuation as a scalar quantity by trees foliage matches physical logic and measurement data and increases as a linear function of frequency and number of leaves. As the frequency increases, the spatial resolution increases, but the phase difference (imaginary component) increases. We solved the dispersion of phase difference by sweeping the frequency and taking the intermediate value.
We developed a microwave foliage scanner based on these basic technology and actual data. This technology is capable of estimating the water content of leaves, predicting the amount of carbon dioxide absorbed, and determining plant health.