I. INTRODUCTION
For many decades ago, the leisure activities on the ocean and river have been dramatically changed due to social demand. The ocean leisure, especially, extended its territory from group activities to individual activities with new technology including electronics power vessel [1]. These vessels have smaller hull size compare to the commercial logistic ship such as crude cargo ship or LNG (Liquified Natural Gas) carrier.
The general size vessel such as LNG carrier can be simulated by BEM (Boundary Element Method) based on potential theory. In the BEM simulation, the vessel motion can be predicted in both of frequency and time domain. For the frequency domain, the motion at each frequency were obtained by using panel method [2]. The time domain simulation used Volterra integral method considering time memory effect [3]. These frequency and time domain simulation were developed with respect to the potential theory which has assumption of irrotational, inviscid and incompressibility [4].
The virtue of potential theory is fast calculation, however, its characteristic such as small amplitude assumption may be useless for small size craft [5]. In this regard, the computational fluid dynamics (CFD) method was employed to simulate small craft behavior under relatively short-wave period. The CFD can estimate force and moments on the floating body properly [5]. However, the grid system may be disturbed due to vessel movement. Therefore, the floating body effects which is radiation and diffraction effects cannot be considered [6]. The only stationary vessel was located at the initial position; thus, it cannot be predicting floating body effect accurately.
Recently, Dynamic Fluid Body Interaction (DFBI) method was introduced including over-set mesh system. The DFBI enables the analysis of vessel when the motion is not known priori [7,8]. When the fluid and external forces act on the vessel, the motion of vessel can be imparted through the over-ser mesh. As results, it is possible to simulate movable object situation without computational error. Moreover, the DFBI contact coupling model allows bodies to collide and rebound from contact which is modeled as a repulsive force [9,10].
In this study, the small craft such as leisure jet board was analyzed with STARCCM+ 15.06. For the analysis, the single-phase problem for shape feasibility, multi-phase problem for resistance and DFBI problem for accurate resistance calculation under real ocean situation were conducted.
II. NUMERICAL MRTHODOLOGY
In this study, STAR-CCM+ 15.06 which is one of most well-known commercial CFD program conducted to simulate flow under regular waves. For the CFD, the continuity and the Navier=Stokes’ equations were employed as governing equations as follows:
where ρ is density, t is time, u is velocity, ∇ is gradient, v is dynamics viscosity coefficient, ∇2 is Laplacian and F is external forces.
When object is located on the free-surface, the free-surface layer can be disturbed due to collision between object and fluid, and then the large deformation of free-surface can be observed. In this case, the flow turns into the turbulence region, thus turbulence model was employed. Among the many models of turbulence, the SST k–ω was chosen. The SST k–ω model is hybrid model which combined k–ω and k–ε model. It has advantage to expect the flow far away from the object and it can be expressed as follows:
where ω is energy dissipation rate, vT is turbulence dynamic viscosity coefficient, σ is Prandtl number of turbulence dissipation rate, C is arbitrary constant and k is turbulence kinetic energy. Because of using turbulence model, the Governing equations can be re-written as follows:
where x is axis of coordination, τ is shear stress, E is energy, T is time scale, H is kinetic energy dissipation rate. Eq. (5). denotes momentum equation for turbulence and Eq. (6). denotes energy equation for turbulence. Both the momentum and energy equations were derived from Navier-Stokes’ equation. The shear stress can be calculated as follows:
where
III. SIMULATION RESULTS
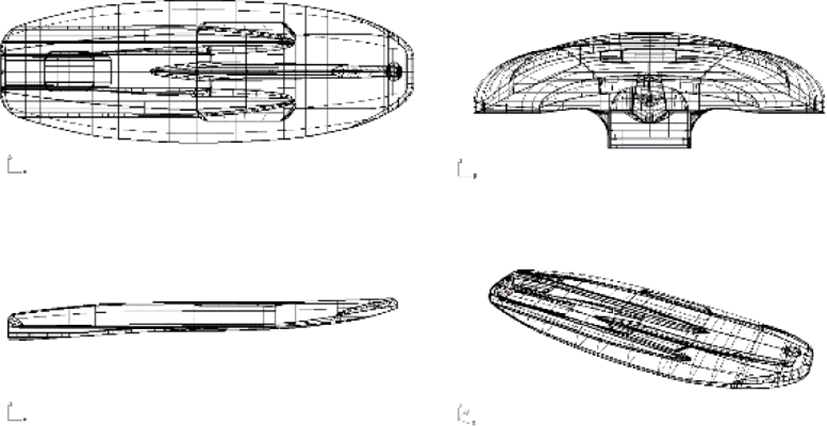
In this study, jet board which is small leisure craft with propulsion system shown in Fig. 1. Fig. 2. represents its schematic model for numerical simulation. The characteristics of jet board is given in Table 1. For the numerical computational domain shown in Fig. 3 has 18L length, 6W width and 20D height where L is length W is width and D is depth of jet board.
For the grid modelling for simulation, Trimmer cell Mesher and prism layer Mesher provided by STARCCM+ were selected. For the calculation approximately 900,000 cells were used and flexible time interval by CFL condition were employed.
In this investigation, there is two stage: firstly, using single phase flow to analyze shape evaluation, and secondly to estimate proper resistance force under regular incidence waves. The specific simulation conditions can be found in Table 2.
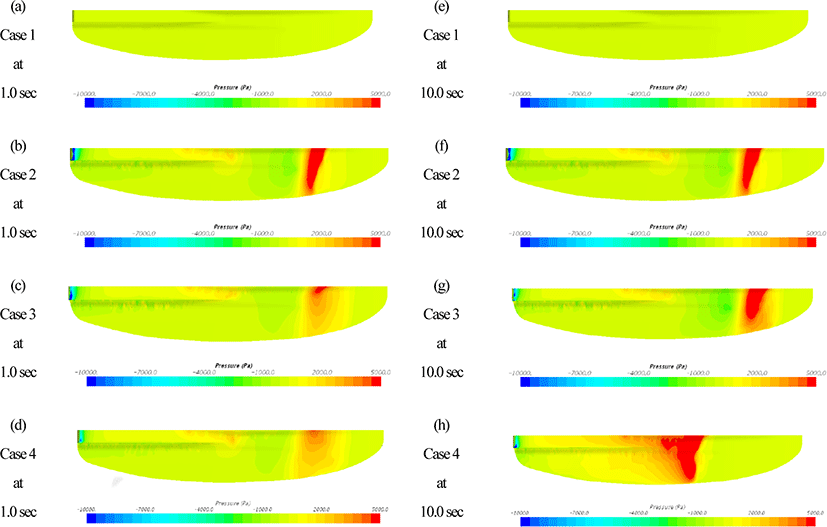
Fig. 4 represents the pressure distribution on the bottom of jet board. Fig. 4 (a)~(d) shows the pressure contour at time 1.0 sec and Fig. 4 (e)~(h) shows the pressure contour at time 10.0 sec. As shown in the Fig. 4, the pressure distribution of case 1 shows that the shape feasibility was obtained. No sudden change of pressure on the body was observed. However, in Case 2-4, the simulation was performed under the condition of real ocean environment including free surface, a concentrated load was observed on the bottom of the vessel. Since the front of the vessel was not attached to the fluid, there is no pressure, however, the concentrated pressure was observed the bottom of vessel due to contacting with free surface.
Comparing Case 2-4, where pressure is generated by contact, they show almost the same aspect in the early stages of the simulation. The difference is that in Case 2, which does not physically create ocean waves, isobars are formed along the free-surface, but in Case 3, make sure that the pressure is concentrated on the keel protrusions. In Case 4, it can be confirmed that the pressure is concentrated in the keel part, and it can be confirmed that the distribution is slightly different from that in Case 3, but the difference was not large in the initial simulation. As can be seen from the comparison in Fig. 4, it was not possible to see the change in the pressure distribution with the time progress compare to Case 2 and 3. In the case of Case 4, it was shown that the position of the concentrated pressure changed in the pressure distribution. Using DFBI, the movement of the fluid distributions were predicted according to the shape and pressure of the wave. It comes to have a substantial movement, and it is caused by the difference in the point where the fluid meets the vessel body. In fact, there is no difference when ocean waves that are relatively small compared to the size of the ship are encountered, but in the case of small ships such as jet boards, changes were considered significantly.
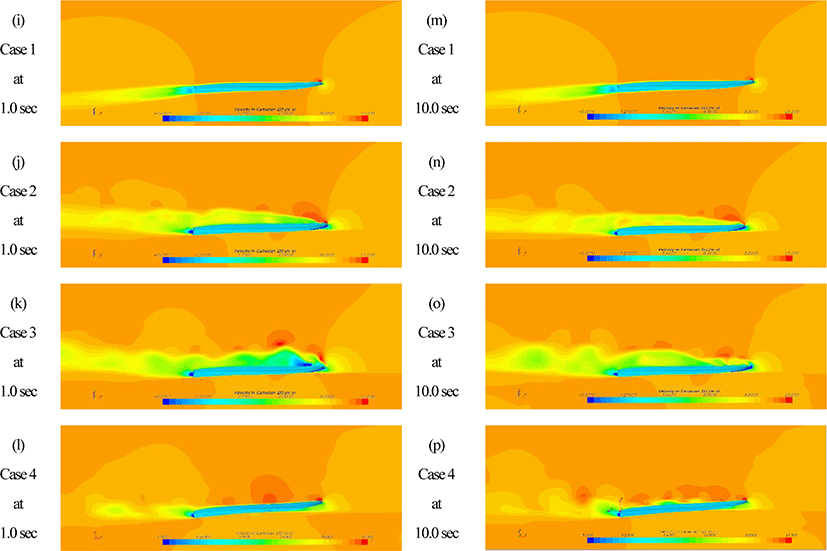
Fig. 5 shows that the velocities of the fluid measured at 5 seconds and 10 seconds from each case. As can be inferred from the pressure comparison, it shows that the laminar flow is formed in Case 1 without a large fluctuation due to the no sudden changes in velocity field which mean there is no disturbance of body motion due to flows. It can be said that the shape of the fluid is well designed. However, in Cases 2 to 4, cases of free surface exists, the phenomenon of air stagnation between the free surface and the partial fluid can be confirmed, and vortices are formed in vessel heading due to these congestions. These vortices mean that the hull design is improper when interpreted solely in Case 2 and Case 3 as being capable of inducing vibrations in the body.
However, in the case of Case 4, which considers the actual movement of the ship, the effect of the trap between the free surface and the body was suppressed by the movement of the ship. The velocity field and streamline were close to that of the Case 1. This is because the change in movement may not be dominant without considering the movement of the ship when reproducing the ocean waves using VOF or first order used in general large ships. There was no problem with large vessel, but it was dominant component to the small craft such as a jet board which does not follow the small amplitude assumption, so it has a great effect on the movement of the hull. According to the Case 2 and Case 3, the shape of vessel was need to be modified considering the suitability of the hull design. However, the result of case 4 which is the simulation under real waves with movable floating body system, there is no point to be modified its shape. It means if researcher follows conventional method, the entire design can be wrong with wrong simulation results, especially small craft.
Table 3 shows the drag and lift in each case. As can be seen from the table, the drag and lift are low when the fluid is assumed to be air even though it is a single-phase flow. In the case of a simulation that considers the free surface that actually operates in a floating body, reproduce the numerical VOF wave instead of the actual wave, and confirm that it came out lower than Cases 3 to 4. This is a study of the force that the slamming effect that occurs when an actual wave meets a negative fluid is not applied, and the floating body is repelled by the reaction force due to collision with the free surface. A comparison of velocity field shows that Case 4 was more stable than Case 3, however, that Case 4 was about 4.5 times higher in terms of practical drag and lift. It is shown that this is difference caused by the change in the angle of impacting the wave while moving abundantly and the generation of room dead force due to the wave, and by this, in the case of small fluid, a method using DFBI in interpreting drag and lift.
IV. CONCLUDING REMARKS
In this study, we predicted the drag and lift of small fluids at sea using a grid-based computational fluid dynamics method. The STAR-CCM + program was used for this study, and studies were conducted under various simulation conditions. When set up for this study, 1) single-phase flow, 2) multi-phase flow (Case of VOF wave and fixed body), 3) multi-phase flow (Case of First order wave and fixed body) 4) multi-phase flow (Case of First order wave and DFBI) was used.
In general, Case 2 or Case 3 conducted to estimate ship drag and lift force. However, in the case of small fluids, it is not possible to establish the small amplitude assumption, so it is important to consider it for the movement of the ship. As a result, the simulation results in each case were compared with the difference due to the pressure distribution and the difference in the velocity field. As a result, the same result that the hull design when the movement of the ship was not taken into consideration was inappropriate was shown. However, in the case of a simulation that considers the movement of the ship using DFBI, it was shown that the flow around the hull appears in the same way as the result of the wind tunnel experiment using single-phase flow.
When comparing the overall cases, in this study, 1) single flow, 2) multi-phase flow VOF Flat wave 3) multi-phase flow f First order wave is assumed and moves at 4 m / s. A flow simulation was performed on the award-winning movement chain jet board.
In the case 1, it is possible to analyze the flow caused by the shape of the object and investigate the overall design. As a conclusion in case 1, in the case of this jet board, the characteristics of a flat board in the general Slender form were clearly shown. it shows that there was no part that caused singular flow with the appearance of an object.
In the case 2, the drag and lift under wave were estimated using the VOF Flat wave. It showed very high drag and lift values compared to a single flow, but it was induced by the free surface effect of this and the increase in pressure due to the crushing that occurs between the free surface and the object.
In the case 3, we used the First order wave to implement waves those were closer to reality than the VOF wave. This confirmed that it was possible to simulate the slamming phenomenon that occurs when the waves were investigated, and then, the pressure increasing was observed. However, in the First order wave, the vortex of air generated in vessel head which promotes turbulence flow. and shows a phenomenon that causes initial separation, and then it may reduce drag force. It was. However, the increased flow due to crushing caused contact surfaces and wakes, the overall drag was higher in the case of the first order wave, and the lift was also higher due to the slamming and free surface effect.
In case 4, DFBI was used for the first order wave to reproduce and simulate more realistically than the previous case 2 and case 3. Both drag and lift force were increases due to movable body and its motion, however, the streamline was more stable than the case 2 and case 3. It shows that case 2 and case 3 claim that the hull design was need to be modified, but the case 4 verified the hull design was perfection as shown in the case 1.
Through the comparison among each case, it was shown that the drag and lift force had significant difference even the same vessel was used. It was revealed that the small craft such as leisure boat or Jet-board DFBI method provided more accurate results. In the future work, the developed DFBI system will be simulate small craft behavior with smart vessel device such as automatic maneuvering and enhanced see-keeping equipment with IoT (Internet of Things) device. It would be very useful to validate the smart device on the vessel to predict its effectiveness numerically.