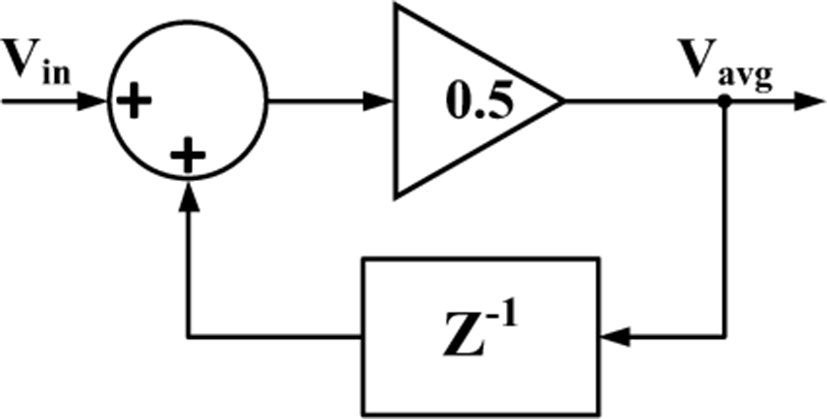
I. INTRODUCTION
The conventional stationary Electrocardiography (ECG) monitoring can reveal harmful cardiac abnormalities; however, it is not feasible for long term non-stationary recording for detecting transient loss of consciousness (T-LOC), lightheadedness or palpitations which occur only once or twice a month or even a few times per year [1]. As a result, for long term and continuous real-time ECG recording, there is an increasing demand for ambulatory ECG monitoring that can effectively record ECG signals while the patient is performing routine activities such as working, exercising or sleeping without interfering with their activities. However, as shown in Fig. 1, the quality of continuous long term ECG monitoring is critically degraded by baseline wander originating from motion artifacts due to various body movements that alters the impedance between the skin and the sensing electrode at the input of the ECG sensor frontend. Baseline wander leads to difficult interpretation of the ECG waveforms, since the basic features (like QRS-Complexes) will not be clearly detectable. As such, tracking and removing the baseline wander is required for proper operation of the continuous real-time ECG monitoring device as it may cause false alarms or wrong event detections that trigger emergency treatments.
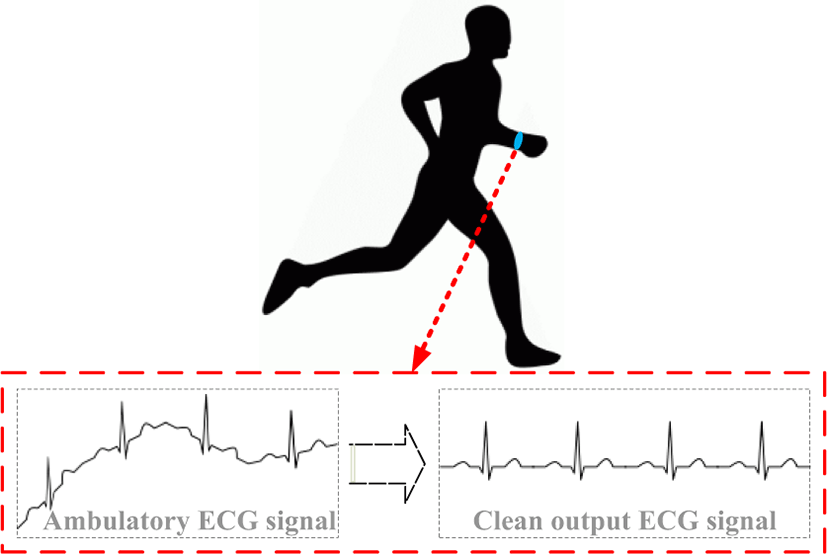
Numerous software and hardware based ECG baseline wander elimination schemes have been presented in the literature including the empirical decomposition method [2], block least mean square (BLMS) algorithm that use motion acceleration as the reference signal [3], and Hilbert vibration decomposition (HVD) [4]. However, the above methods rely on post processing of the corrupted ECG waveforms, thus are not suitable for continuous real-time monitoring. Meanwhile, adaptive filter [5] and independent component analysis (ICA) [6] based hardware schemes are available, but these require additional components such as micro-controllers, FPGAs, ADCs, and DACs which increases the power consumption and form factor of the ECG monitoring device.
Nowadays, Brain-Computer Interfaces (BCI) which use artificial intelligence (AI) algorithms such as deep learning [7] are widely utilized in recording ECG/EEG signals and recognizing their features. However, a hybrid classifier model used in [8] and a pattern-based authentication method utilized in [9] need long short-term memory along with recorded EEG/ECG waveforms to classify the upcoming signals for noise reduction. These approaches impose latency between different hardware modules, high computation, more area and power consumption to the whole systems. In this paper, a fully analog baseline wander tracking and removal circuitry is proposed. The proposed circuitry that can be incorporated within the ECG sensor frontend without using digital post processing, is suitable for continuous real-time ECG monitoring devices. In addition, the baseline wander in ECG waveforms corrupted by various motion artifacts can be effectively tracked and removed, whereas minimizing the loss of essential features including the QRS-Complex. This paper is organized as follows. Section 0 describes the proposed ECG baseline wander tracking and removal scheme. The circuit implementation and simulation results are shown in section III and IV, followed by the conclusions in section V.
II. ECG BASELINE WANDER TRACKING AND REMOVAL
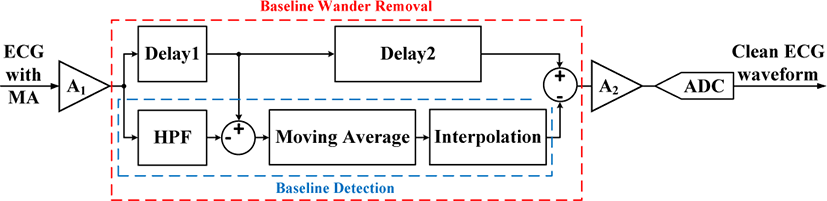
The proposed ECG baseline wander tracking and removal scheme can be easily incorporated in the sensor frontend. Fig. 2 shows the block diagram of the proposed circuitry which includes two delays, baseline detection block, and the subtractor. Once the corrupted ECG signal is amplified by A1, it will go through the baseline detector that extracts the baseline wander which is subtracted from the delayed version of the corrupted signal to generate a clean waveform. The final output is then amplified by another gain stage A2 for further processing. The basic concept of baseline wander detection is taking the moving average of the corrupted ECG signal. The baseline detector consists of the high pass filter (HPF), moving average and interpolation blocks. The HPF passes high frequency (HF) components of ECG signal in particular, the R-peaks, and attenuates low frequency (LF) components - motion artifacts and DC-offset. However, the capability of the HPF for attenuating LF components and passing HF components such as the R-peaks will depend on the filter order. Therefore, subtracting the HPF output from the corrupted ECG waveform will exclude R-peak samples from the moving average, where Delay1 is used for compensating the HPF delay. This will prevent distortion in the baseline wander tracking caused by the R-peaks, once they are included in the moving average. Finally, the baseline wander is extracted by linearly or quadratically interpolating the HF components excluded down sampled moving average, and subtracted from the delayed version (through Delay2) of the corrupted ECG waveform to generate a clean ECG signal.
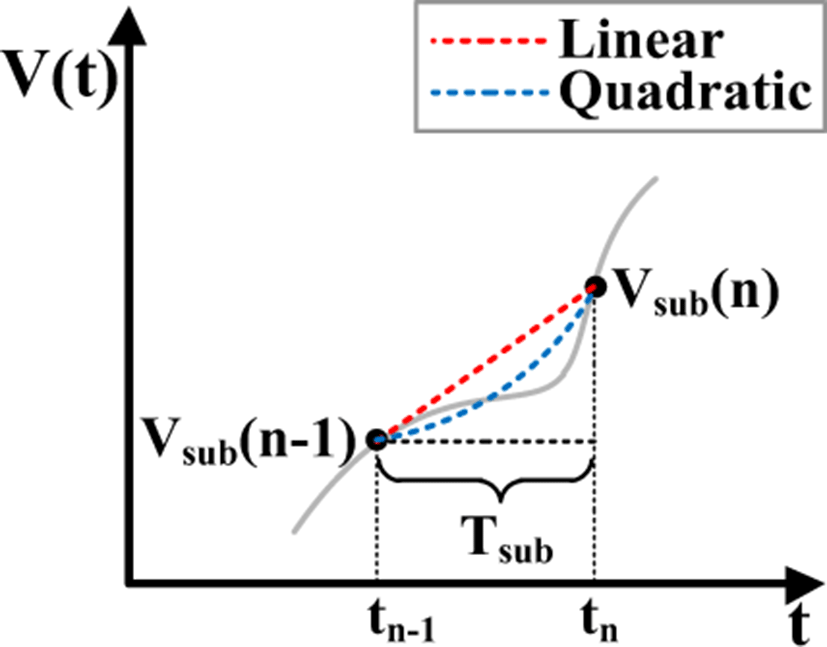
Fig. 3 shows the concept of linear and quadratic interpolation methods used in the proposed approach to track the baseline wander in corrupted ECG signals. The baseline level of the incoming ECG signal from moving average is obtained by continuous linear or quadratic interpolations of the two data points Vsub(n-1) and Vsub(n) within the time interval Tsub. In this case, the baseline level VLerp, VLinear and the quadratic interpolation output VQuad between time tn-1 and tn can be expressed as:
This will lead to linear and quadratic curves that connect the two points Vsub(n-1) and Vsub(n). Therefore, the final equations for linear and quadratic interpolations are as follows:
Fig. 4 shows how the baseline wander is extracted from the corrupted ECG signal to obtain a clean waveform [10].
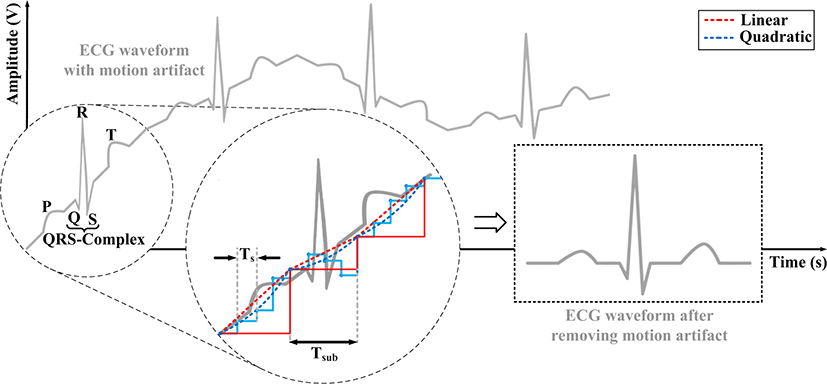
The moving average excluding the R-peaks and HF components sampled with fs (=1/Ts) (the blue solid line waveform) is down sampled with fsub (= 1/Tsub), which results in the red solid waveform where generally, fs > fsub. The down sampled moving average is interpolated with linear or quadratic methods, where the red and the blue dotted waveforms shows the result of linear and quadratic interpolation, respectively. Since quadratic interpolation will better represent the baseline wander, quadratically interpolating the down sampled moving average will lead to improved baseline wander tracking compared to linearly interpolating the data points. The final clean output waveform will be obtained by subtracting the detected interpolated data points from the corrupted ECG waveform.
III. CIRCUIT IMPLEMENTATION
The proposed baseline wander tracking and removal circuitry which includes the HPF based R-peak detection and quadratic interpolation is designed using CMOS 0.18-μm technology with supply voltage of 1.8 V.
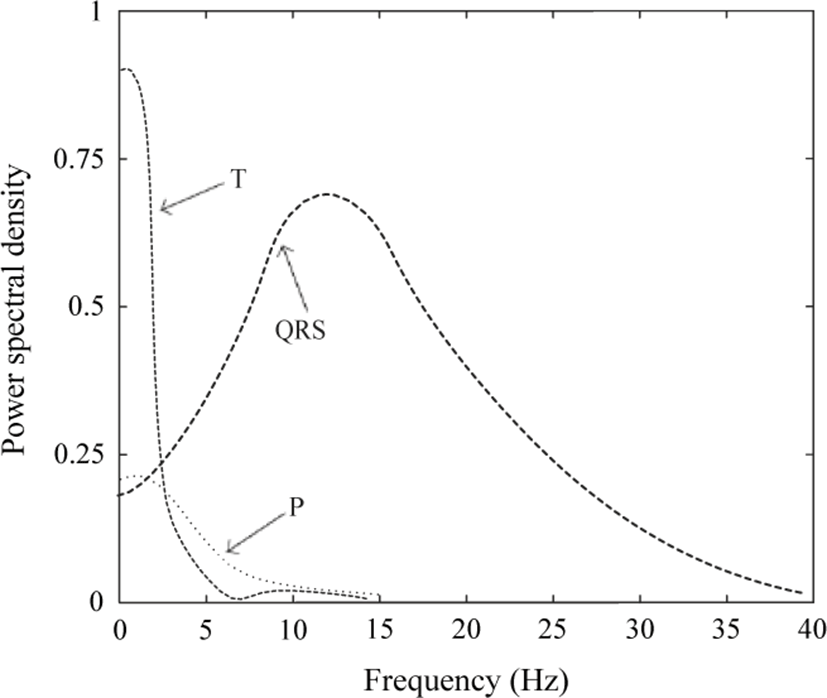
The HPF should effectively pass QRS-Complex of ECG signal and suppress LF components, thus the filter cut-off frequency should be set based on the frequency spectrum of the ECG signal. According to Fig. 5 presented in [11], QRS-Complex can be well preserved by setting the cut-off frequency of HPF around 10-15 Hz, where the proposed filter is designed based on this assumption. However, it should be noted that increasing the order of HPF will further attenuate LF components of ECG signal which results in better R-peaks detection. Therefore, with a higher order filter, R-peaks are better excluded from moving average by subtracting the HPF output from the delayed version of corrupted ECG signal. In addition, the P- and T-waves will be excluded from the baseline wander through down sampling and interpolating the moving average. The z-domain transfer function of the 4-th order HPF is given as:
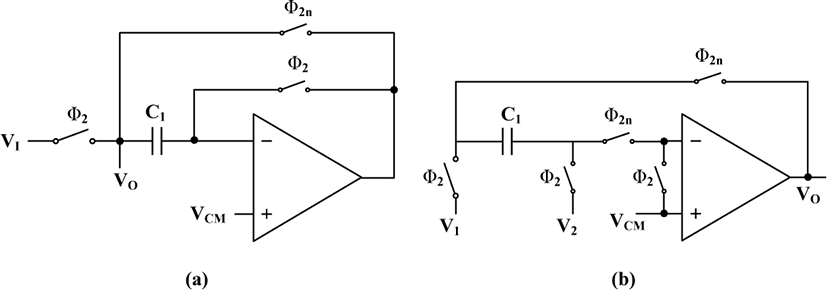
where a, b, c, d and e coefficients are set to achieve 10-15 Hz cut-off frequency and attenuate LF components while keeping the filter stable. Fig. 6(a) shows the z-domain representation of the HPF which includes delays (z-1), gain stages, and adders, and Fig. 6(b) shows the switch capacitor (SC) implementation of the 4th order HPF, where the four adders are combined into one single adder with five inputs. Furthermore, the gain stages (a to e) are realized by adjusting the ratio between each input capacitor and the feedback capacitor (C). However, since the coefficients a to e can be either negative or positive, their signs are inverted by swapping the control clock of the first two switches. As a result, the positive and negative coefficients can be implemented by setting the adder to a non-inverting or inverting SC summing configuration.
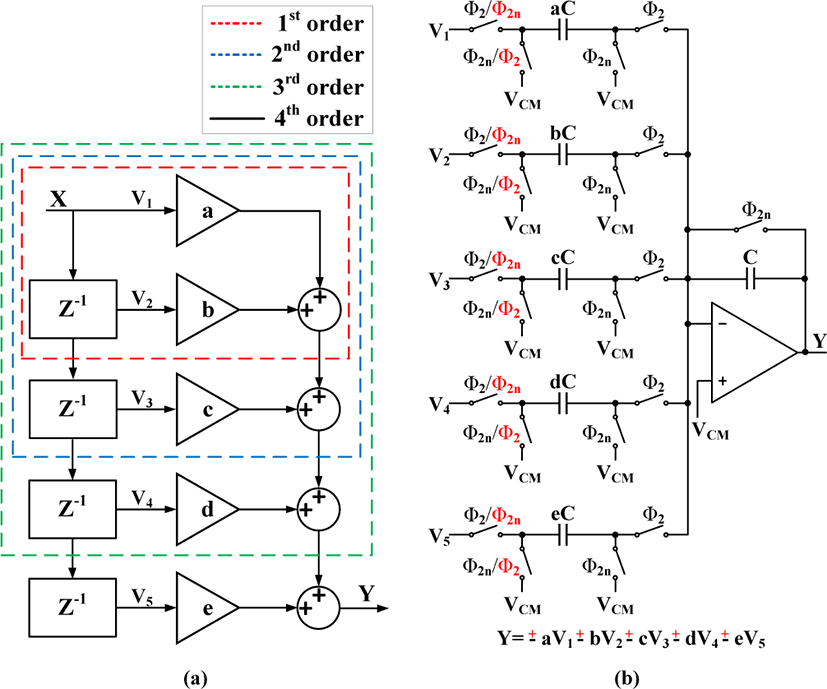
Fig. 7(a) shows the track and hold (T/H) or delay (z-1) circuit that operates in two modes. In the track mode (Ф2 = H and Ф2n = L), the input is sampled at C1 and the output tracks the input (VI=VO). In the hold mode (Ф2 = L and Ф2n = H), the input is disconnected and the output shows the last value sampled in C1. Fig. 7(b) shows the subtractor which is utilized to subtract the HPF output from the delayed version of corrupted ECG signal. The signal V2 is subtracted from V1 in phase Ф2 and the result will be kept and sent to the output during phase Ф2n. The OTA used in the ECG baseline detection block is a rail-to-rail folded cascode configuration with DC gain of 61 dB and GBW of 12.9 MHz, and power consumption of 290 nW.
The moving average circuit is shown in Fig. 8 in which it is comprised of an adder, a gain stage and delay. The adder and gain block are combined together same as the circuit shown in Fig. 6(b) but with two inputs where the input capacitors are half of the feedback capacitor (C) to satisfy 0.5 gain value. The delay block is also similar to Fig. 7(a).
The quadratic interpolation block shown in Fig. 9(a) is realized using linear interpolation, subtractor, delay, offset cancellation, integrator and gain stage circuits. In the ideal behavioral model, the delay (z-1) and offset cancellation circuits are not required. However, in the actual circuit, the delay block is used to compensate the delay generated by the subtractor in linear interpolation circuit and synchronize the signals VLinear and Vsub(n-1). In addition, the offset cancellation circuit removes the offset produced by the integrator coming from linear interpolation circuit. Overall, the blue dashed block in Fig. 9(a) implements eq. 1(c), which leads to the blue dotted waveform shown in Fig. 4. In this design, first, the delayed input (Vsub(n-1)) is subtracted from the linearly interpolated data (VLinear), which leads to VLerp as shown in eq. 1(b). Next, after removing the offset from VLerp, integrating with a gain of 2/Tsub, and adding the presented initial value (Vsub(n-1)), the VQuad signal corresponding to eq. 1(c) or eq. 2(b) is generated.
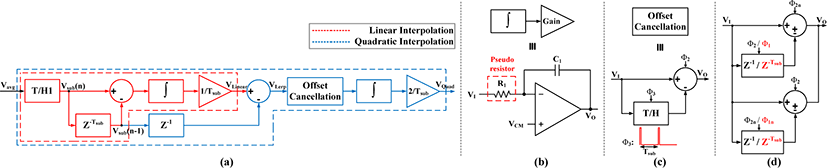
The linear interpolation circuit is presented in [10]. The subtractor and delay circuits of quadratic interpolation block are same as Fig. 7. The integrator with the gain stage is implemented with a continuous time integrator as shown in Fig. 9(b), which consists of the pseudo resistor, capacitor and OTA. The pseudo resistor is in order of tens of Giga-ohm to enforce the capacitor becomes on-chip and satisfy the gain value of 2/Tsub. Next, the offset cancellation circuit is indicated in Fig. 9(c) where it contains a T/H and a subtractor. The T/H circuit works with clock Ф3 with frequency of fsub and 1% duty cycle. Therefore, initial data point of VI (in Fig. 9(c)) is sampled, kept and reduced from the upcoming VI signal for every Tsub cycle that generates VO without offset. Lastly, the combination of adder/subtractor and delay circuits in the whole system operate in pipeline fashion as shown in Fig. 9(d). In this way, the signal can be tracked and followed for the whole clock cycle. This combination in the linear interpolation circuit uses Ф1 and Ф2 which are set to fsub/2 and fs/2, respectively with duty cycle of 50%, where Ф1n and Ф2n are the inverted version of Ф1 and Ф2. However, the delay (z-1) and the T/H circuit in the other parts operates with Ф2 clock signal, identical to the adder/subtractor.
IV. SIMULATION RESULTS
The proposed ECG baseline wander tracking and removal circuitry is verified through circuit level simulation. The optimum value of fsub is set to 4 Hz, however, increasing fsub will remove more useful components of ECG signal such as the QRS-Complex from the clean ECG output waveform. On the other hand, if fsub is set lower than 4 Hz, the baseline wander cannot be accurately tracked. Furthermore, the optimum value of fs is set to 40 Hz, therefore the sampling rate of Ф1 and Ф2 clock results in 2 Hz and 20 Hz with 50% duty cycle. The sampling rate of Ф3 clock is set to 4 Hz with 1% duty cycle. The a-e coefficients of the 4th order HPF are set to -0.08, -0.26, 0.67, -0.26 and -0.08 respectively. Fig. 10(a) shows the waveforms obtained from the proposed ECG baseline wander tracking and removal circuitry with the 4th order HPF and quadratic interpolation circuit. The gray waveform is the corrupted ECG signal (with delay), the blue waveform is the HPF output (with level shifted for clear view), red waveform is the extracted baseline wander, and the black waveform is the clean ECG signal generated from the proposed circuit. As shown, the final output waveform does not contain baseline wander and DC offset, whereas the key features of the ECG signals are well preserved. It should be noted that by increasing the order of HPF, the R-peaks are extracted more accurately while LF components are better attenuated. However, the odd-order HPFs which intrinsically contain odd number of adders/subtractors and delay elements, produce huge negative glitches when the R-peaks pass through the filter, which degrades the SNR improvement. Meanwhile, even-order HPFs well preserve the R-peaks without producing much negative glitches. Fig. 10(b) shows the detected baseline wander (with level shifted for better view) after moving average stage with (the red waveform) and without (the blue waveform) using HPF to exclude R-peaks. Without the HPF, the moving average will not represent the true motion artifact due to the huge R-peak samples included in the moving average input, thus will distort the clean ECG waveform once the output of the interpolated down sampled moving average is subtracted from the corrupted ECG signal.
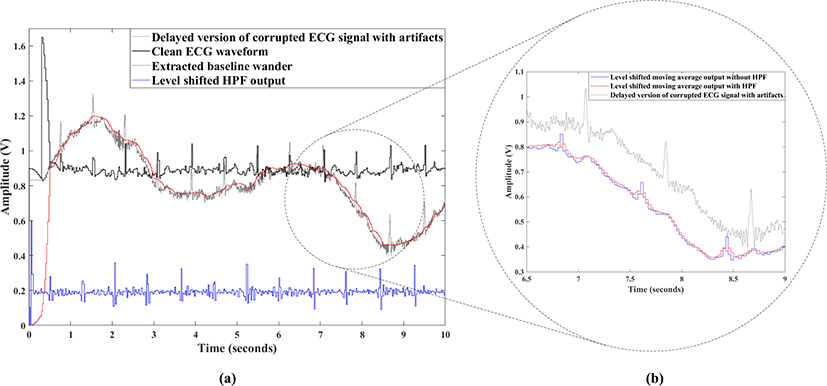
Table 1 shows the performance comparison results for distinct filter types/orders and interpolation methods. It is obvious that power consumption and estimated area will increase in accordance with elevating the HPF order and using advanced interpolation methods. As a result, using the 4th order HPF with the quadratic interpolation method shows the highest SNR improvement, whereas the 2nd and 3rd order HPFs show comparable results. In addition, the linear interpolation method leads to less area and lower power consumption compared to its quadratic counterpart, even though the quadratic interpolation method shows higher SNR improvements in many cases. However, the entire ECG baseline detection block can be replaced by a low-pass filter (LPF) that can track the baseline wander to a certain degree. Although this approach achieves the lowest power consumption and area, the accuracy of detecting the baseline wander (SNR improvement) is decreased drastically in comparison to other cases. This indicates simply using the LPF to extract the baseline wander from the corrupted ECG signal, instead of interpolating the down sampled moving average excluding the HF components will put more useful ECG features in the extracted baseline wander which will be subtracted from the corrupted ECG signal, thus resulting in a poor SNR improvement. Table 2 shows the performance of presented work with 4th order HPF and quadratic interpolation compared to existing hardware-based baseline wander elimination schemes. It is clear that this work reduces the power consumption and chip area drastically while removing motion artifacts effectively.
| Ref | [6] | [12] | This work |
|---|---|---|---|
| Technology | 0.13 μm CMOS | 0.18 μm CMOS | 0.18 μm CMOS |
| Supply | 1.2 V | 1.2 V | 1.8 V |
| Power | 46-73 μW + FPGA |
374 μW + ARM Cortex-M0 |
19.14 μW |
| Area (IC only) | 2.35×2.38 mm2* | 7×7 mm2** | 3.4×4.6 mm2 *** |
| Motion Artifact Elimination | can handle 17×larger amplitude | SAR improvement 8-10 dB | SNR improvement 9.96 dB |
V. CONCLUSION
In this paper, a fully analog circuit which tracks and removes baseline wander from ECG signals corrupted with motion artifacts is presented. The baseline wander is extracted by down sampling the moving average obtained from the corrupted ECG waveform, and quadratically interpolating it, where the HPF is used to exclude the R-peak samples from the moving average. The clean ECG waveform is generated by subtracting the detected baseline wander from the delayed version of the corrupted ECG waveform. Simulation results show the proposed circuit can effectively track and remove baseline wander from ECG waveforms corrupted with motion artifacts, where the 4th order HPF along with quadratic interpolation structure has the best performance - SNR improvement around 10 dB. The proposed circuit can be realized with low power and small area, thus can enable a very compact and energy efficient ambulatory ECG monitoring platform.